由“Poisson回归分析-理论介绍”可知,对于服从Poisson分布的计数变量,可以采用Poisson回归进行影响因素分析,此时,事件的发生是独立的,计数值的平均数等于方差。然而,一些事件,如地方病、遗传性疾病、传染性疾病的发生和分布是非独立的,个体事件发生的概率不等。这类资料的平均数远小于方差,存在过离散现象。若用Poisson回归来分析这些事件的影响因素,会导致模型参数估计值的标准误偏小,参数检验的假阳性率增加。因此,普遍认为对于有聚集现象或方差大于均数的计数资料的分析,不宜采用Poisson回归,宜选用负二项回归(Negative binomial regression)模型。目前,负二项回归多应用于车祸次数、卫生服务利用等方面。本文将举例介绍负二项回归的相关理论。
关键词:负二项回归; 过离散
一、基本概念
对于某些计数资料,当其服从的Poisson分布强度参数λ服从γ分布时,所得到的复合分布即为负二项分布,又称为γ-Poisson分布(gamma-Poisson distribution)。在负二项分布中,λ 是一个随机变量,方差λ(1+kλ)远大于其平均数。其中,k为非负值,表示计数资料的离散程度。当趋近于0时,则近似于Poisson分布,过离散是负二项分布相对于Poisson分布的重要区别和特点,可用拉格朗日算子统计量检验资料是否存在过离散。若数据服从Poisson分布可以采用Poisson回归;当计数因变量服从负二项分布时,可采用负二项回归进行回归分析,其参数估计、假设检验与Poisson回归相似。
假设yi表示单位时间内事件发生的频数,呈现负二项分布,则模型方程如下:
\(\ln \left(\widehat{y}_{l}\right)=\log \left(n_{i}\right)+\beta_{0}+\beta_{1} X_{i 1}+\beta_{2} X_{i 2}+\cdots+\beta_{m} X_{i m}+\log k_{i}\)
负二项回归模型的参数估计及意义、假设检验及拟合优度检验等与Poisson回归类似。
二、适用条件
负二项回归至少需要满足以下2个条件:
条件1:各观测行间是非独立的,事件的发生有空间聚集现象。
条件2:因变量存在过离散现象,即方差远大于均数。
三、案例数据
某市抽样调查了146名学生某一学年的缺课天数(Days),同时收集了他们的种族(Race,1=汉族、2=少数民族)、性别(Sex,1=男、2=女)、年龄(Age,1=小于12岁、2=小于10岁、3=小于8岁、4=小于6岁)和学习状况(Study,1=良好、2=一般)等信息,拟探究上述因素对学生缺课天数的影响。部分数据见图1
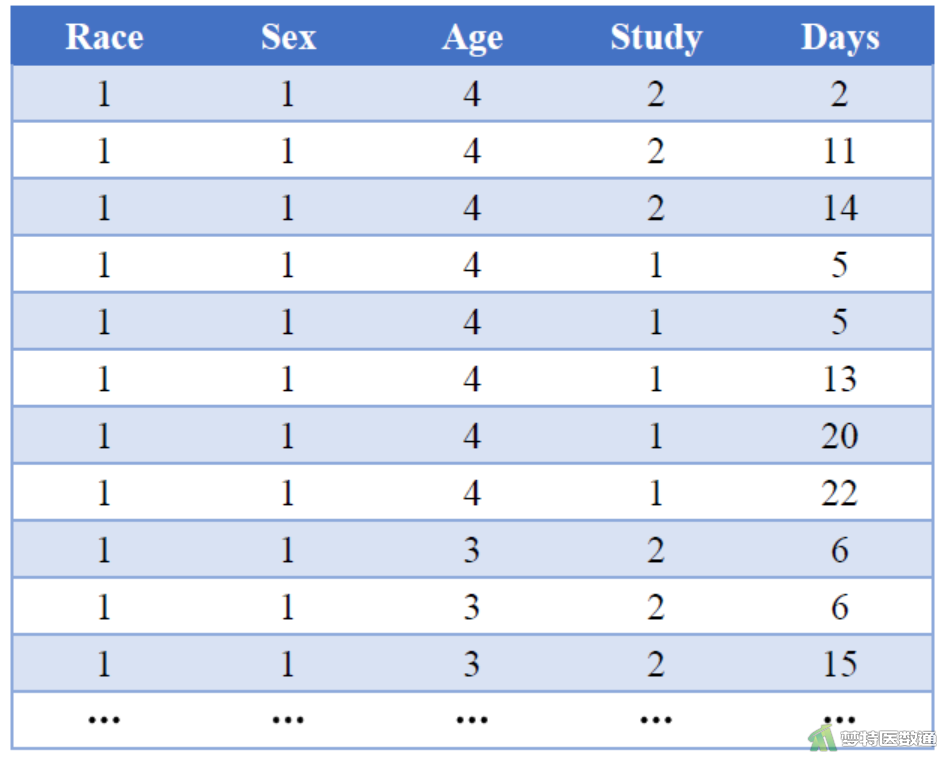
四、假设检验
(一) 回归模型的检验
1. 建立假设检验,确定检验水准
H0:β1=β2=β3=β4
H1:βm (m=1、2、3、4)不全为0
α=0.05
2. 计算检验统计量
通过软件可得到负二项回归模型的似然比统计量为χ2=21.807。
3. 确定P值,做出统计推断
统计量服从自由度为6的χ2分布。由此可确定,P=0.001,即模型整体有统计学意义。
(二) 回归系数的检验
对每个自变量的回归系数进行检验,即判断每个自变量的回归系数是否为0。
1. 建立假设检验,确定检验水准
H0:βm =0
H1:βm≠0
α=0.05
2. 计算检验统计量
通过统计分析软件可得到每个自变量对应的Wald χ2、截距、每个自变量的哑变量对应的回归系数,详见图2。
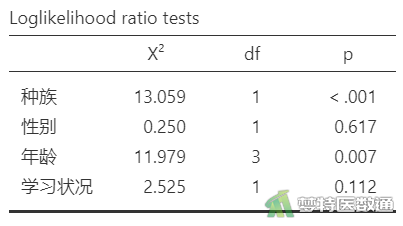

3. 确定P值,做出统计推断
由图2可知,四个自变量中种族和年龄有统计学意义(P<0.05)。由图3可知,相对于汉族,少数民族学生的回归系数为0.566,P<0.001,表示少数民族学生缺课的发生率是汉族学生的0.566倍(IRR=0.566, 95%CI:0.415-0.770)。年龄6-8岁的与10-12岁的相比,缺课的发生率下降了0.553倍(IRR=0.447, 95%CI:0.275-0.725,P=0.001),关联有统计学意义。