Pearson偏相关性分析(Pearson Partial Correlations Analysis)——SAS软件实现

关键词：SAS; 偏相关分析; 偏相关系数

一、案例介绍

某高血压研究所收集了110例高血压患者的临床资料，包括年龄、BMI、同型半胱氨酸(Hcy)、胆固醇、尿酸(UA)和24小时收缩压标准差(24hSSD)和24小时收缩压变系数(24hSCV)等，研究Hcy与24hSSD或24hSCV的相关性。经过前期分析发现，Hcy、UA和24hSSD有相关性，现欲了解控制UA的影响后，Hcy与24hSSD的相关性。部分数据见图1。本文案例可从“附件下载”处下载。其中，UA是高血压患者的尿酸，Hcy是高血压患者的同型半胱氨酸，_24hSSD是高血压患者的24小时收缩压标准差(因为SAS中无法以数字作为变量名的开始，所以默认在前面加上下划线“_”进行区分)。

二、问题分析

本案例的分析目的是考察控制某因素的影响后，两个连续性变量之间的相关性，可以使用Pearson偏相关性分析。但需要满足以下6个条件：

条件1：两个变量均为连续变量。本研究中Hcy与24hSSD均为连续性变量，该条件满足。

条件2：样本独立性。样本来自总体的随机样本，且被试者之间必须相互独立，该条件满足。

条件3：两个变量及需要控制的变量应当是配对的，即来源于同一个体的特征或属性。本案例中同时检测了研究对象的同型半胱氨酸、尿酸和24小时收缩压标准差，变量之间是对应关系，该条件满足。

条件4：两个变量服从正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件5：两个连续变量之间存在线性关系，该条件需要通过软件分析后判断。

条件6：两个变量都不存在明显的异常值，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件4判断(正态性检验)

(1) SAS实现

首先导入数据，代码如下：

proc import datafile="G:\test\偏相关分析.csv" dbms=csv out=data1;
run;

使用如下的univariate过程步，对同型半胱氨酸(Hcy)与24小时收缩压标准差(24hSSD)变量进行正态性检验：

proc univariate data=data1 normal;
	var Hcy _24hSSD;
run;

其中，normal选项表示对变量做正态性分析。

(2) 结果解读

图2和图3分别列出了同型半胱氨酸(Hcy)与24小时收缩压标准差(24hSSD)变量的正态性检验结果。Shapiro-Wilk正态性检验的P值分别为0.533、0.836，均>0. 1，提示两变量均服从正态分布。因此，本案例满足条件4。

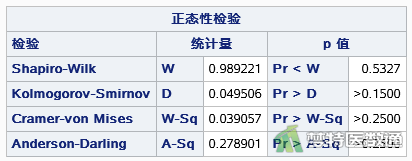
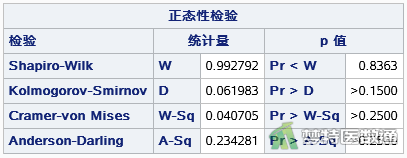
2. 条件5判断(线性关系分析)

(1) SAS实现

proc sgplot data=data1;
	scatter x=_24hSSD y=Hcy;
run;

(2) 结果解读

图4为同型半胱氨酸(Hcy)与24小时收缩压标准差(24hSSD)的散点图，散点大致呈一条直线，说明存在线性关系，即本案例数据满足条件5。

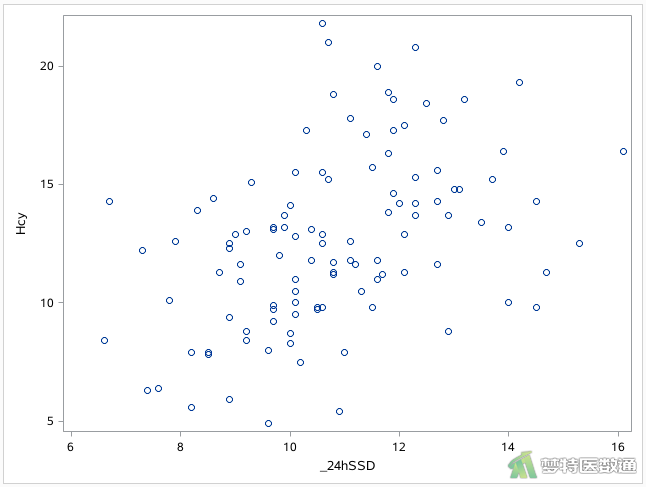
3. 条件6判断(异常值判断)

(1) SAS实现

使用如下的proc univariate过程步，可以获得同型半胱氨酸(Hcy)与24小时收缩压标准差(24hSSD)变量的描述性统计量(均值、标准差、最大最小值等)、绘制箱线图等结果：

proc univariate data=data1 plot;
	var Hcy _24hSSD;
run;

(2) 结果解读

图5和图6分别展示了同型半胱氨酸(Hcy)变量的百分位数、直方分布图和箱线图，最大值和最小值分别是21.8和4.9 μmol/L，首先从专业角度可判断是在正常值范围内；其次，观察箱线图，我们也可以发现并无异常点出现，因此同型半胱氨酸(Hcy)变量无异常值。

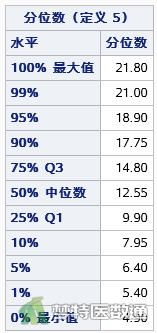
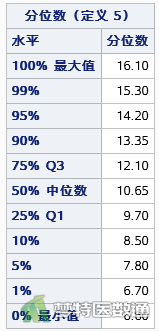
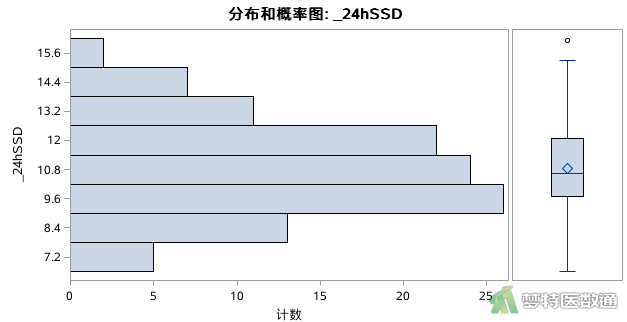
图7和图8分别展示了24小时收缩压标准差(24hSSD)变量的百分位数、直方分布图和箱线图，最大值和最小值分别是16.1和6.6 mmHg，首先从专业角度可判断是在正常值范围内；其次，观察箱线图，我们可以发现有一个异常点出现，但考虑到最大值和最小值均在正常值范围内，所以不需要对异常值进行处理。

综上，本案例未发现需要处理的异常值，满足条件6。

(二) 统计描述及推断

1. SAS实现

proc corr data=data1 pearson;
	var Hcy _24hSSD;
	partial UA;
run;

其中，partial用于指定要校正的变量。

2. 结果解读

(1) 统计描述

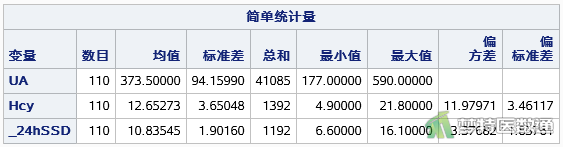
如图9所示，高血压患者的同型半胱氨酸(Hcy)水平为12.653±3.650 μmol/L，24小时收缩压标准差(24hSSD)为10.835±1.902 mmHg，尿酸(UA)为373.500±94.160 μmol/L。

(2) 统计学推断

如图10所示，控制尿酸(UA)后，同型半胱氨酸(Hcy)与24小时收缩压标准差(24hSSD)之间的偏相关系数r =0.370，P<0.0001。即控制了尿酸(UA)的影响后，同型半胱氨酸(Hcy)与24小时收缩压标准差(24hSSD)呈正相关，且有统计学意义。

四、结论

本研究采用Pearson偏相关分析判断在控制高血压患者的尿酸水平时，患者同型半胱氨酸水平和24小时收缩压标准差是否有关。已知两个变量均为连续变量，样本独立，且两个变量及需要控制的变量分别来自同一个体；通过正态性检验发现两个变量服从正态分布；通过散点图发现，两个变量之间存在线性关系；通过箱线图及专业知识判断，数据不存在需要处理的异常值。

描述性分析结果显示，高血压患者的同型半胱氨酸(Hcy)水平为12.653±3.650 μmol/L，24小时收缩压标准差(24hSSD)为10.835±1.902 mmHg，尿酸(UA)为373.500±94.160 μmol/L。Pearson偏相关分析结果显示，控制尿酸(UA)后，同型半胱氨酸(Hcy)与24小时收缩压标准差(24hSSD)之间的偏相关系数r =0.370，P<0.0001。综上，控制了尿酸(UA)的影响后，同型半胱氨酸(Hcy)与24小时收缩压标准差(24hSSD)呈正相关。

五、分析小技巧

(一) 偏相关分析

• 偏相关分析也称净相关分析，是指当两个变量同时与第三个变量相关时，将第三个变量的影响剔除，只分析要探索的两变量间的相关程度的过程。当控制变量个数为1时，偏相关阶数为1；当控制变量个数为2时，偏相关阶数为2。偏相关分析包括Pearson偏相关性分析(适用于正态分布的计量资料)、Spearman偏相关性分析(适用于非正态分布的计量资料或总体分布未知的变量)和Kendall's tau-b偏相关性分析(适用于等级资料)。

(二) 偏相关系数

• 偏相关系数和简单相关系数的区别在于前者进行了变量控制；共同点在于两者都是表示两个随机变量之间线性相关程度和方向的统计量。r>0，为正相关；r<0，为负相关。r的绝对值大小表示两变量之间线性相关的密切程度。一般当0.9</r/<1，为高度相关；当0.7</r/<0.9，为强相关；0.4</r/<0.7，为中度相关；0.2</r/<0.4，为弱相关性；0</r/<0.2，为极弱相关或无相关性。但相关系数强弱的判断标准，对于不同专业存在差异，使用时需要结合专业背景综合决定。