独立样本Wilcoxon秩和检验 (Wilcoxon Rank Sum Test)——R软件实现

关键词：R语言; R软件; 非参数检验; 秩和检验; Wilcoxon秩和检验; 独立样本秩和检验; Mann-Whitney U检验

一、案例介绍

某医师对12例高血压患者和11例糖尿病患者血清总胆固醇(TCHO)含量(mmol/L)进行了测定，问高血压患者和糖尿病患者的血清总胆固醇含量是否不同？部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较两组计量资料是否有差异，即判断高血压患者和糖尿病患者的血清总胆固醇含量是否不同。比较两组计量资料是否有差异可以使用两独立样本t检验或Wilcoxon秩和检验检验。如果数据满足正态性和方差齐性要求则可以使用两独立样本t检验。若满足正态性，不满足方差齐性，可使用校正t检验(Welch’s t检验)。但如果数据的方差相差太大，最好使用非参数检验(Wilcoxon秩和检验)。如果数据正态性和方差齐性都不满足，最好使用非参数检验(Wilcoxon秩和检验)。Wilcoxon秩和检验，需要满足3个条件：

条件1：有一个观察变量，且观察变量为连续变量(不满足正态分布或方差严重不齐)或等级变量。该条件需要通过软件判断或专业判断。

条件2：有一个分组变量，且为二分类。本研究中分为高血压患者组和糖尿病组，该条件满足。

条件3：具有相互独立的观测值。本研究中各研究对象的TCHO含量都是独立的，不存在互相干扰的情况，该条件满足。

三、软件操作及结果解读

(一) 导入数据

mydata <- read.csv("Wilcoxon秩和检验.csv")  #导入CSV数据
View(mydata)  #查看数据

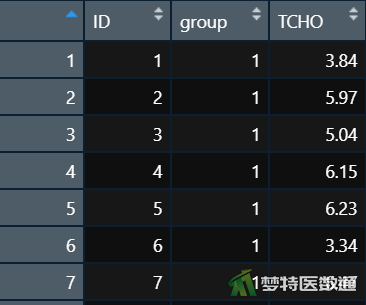
在数据栏目中可以查看全部数据情况，数据集中共有3个变量和23个观察数据，3个变量分别代表被调查者的编号(ID)、分组(group)及血清总胆固醇含量(TCHO)。
如果数据集较大也可使用如下命令查看数据框结构：

str(mydata) #查看数据框结构

(二) 适用条件判断

1. 条件1判断(正态性检验)

(1) 软件操作

Wilcoxon秩和检验时，需要分别考察每一组数据的正态性情况，因此需要拆分数据。
##拆分数据##

mydata1<-subset(mydata, mydata$group==1)  #按组生成数据子集1
mydata2<-subset(mydata, mydata$group==2)  #按组生成数据子集2

##分组描述数据子集##

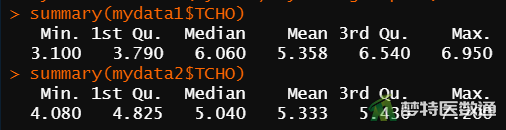
summary(mydata1$TCHO)  #描述子集1基本情况
summary(mydata2$TCHO)  #描述子集2基本情况

##分组查看缺失值情况##

is.na(mydata1$TCHO)  #查看子集1有无缺失值
is.na(mydata2$TCHO)  #查看子集2有无缺失值

##绘制Q-Q图##

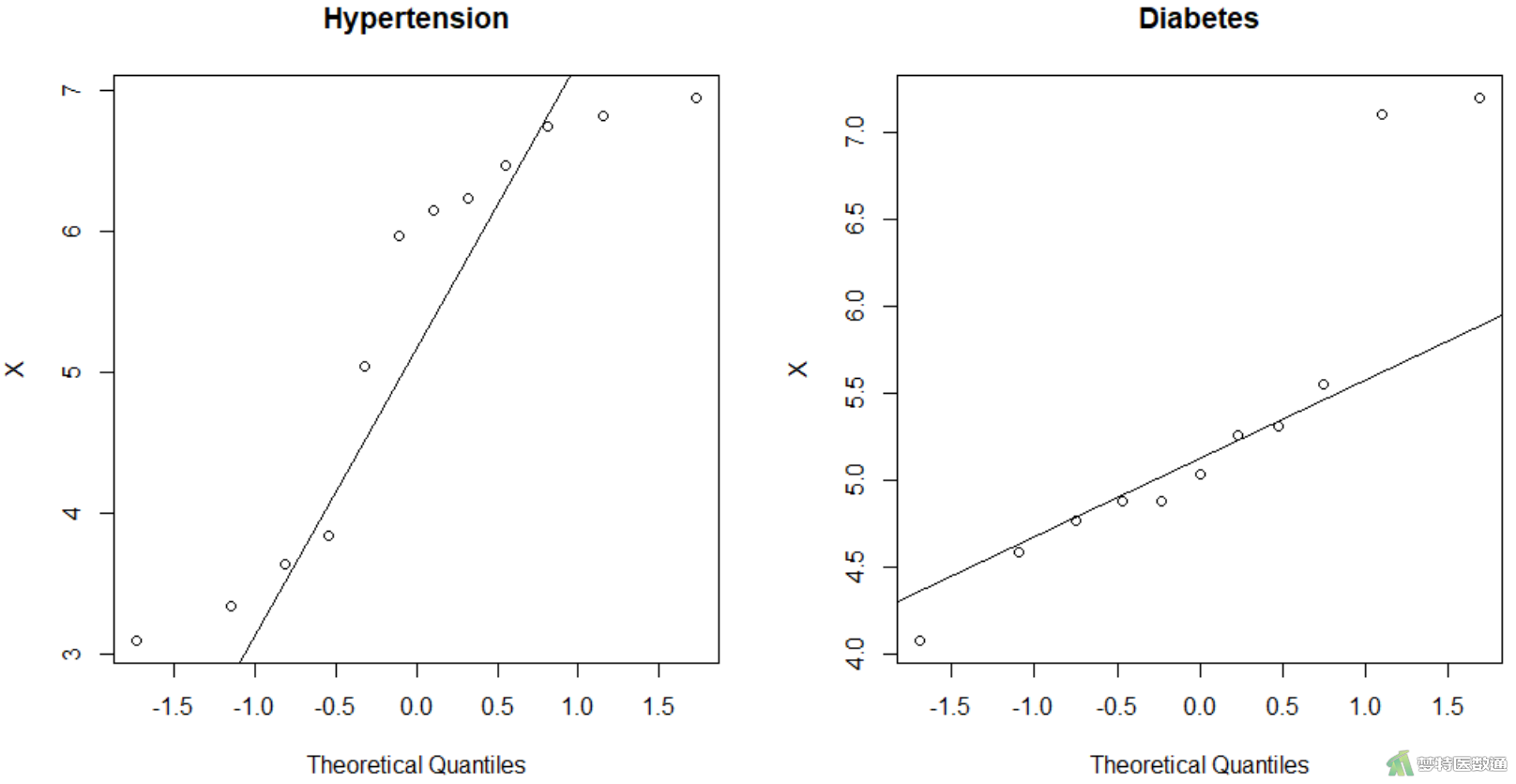
par(mfrow = c(1, 2))  #设置画1行2个图片
qqnorm(mydata1$TCHO, ylab="X", main="Hypertension")  #绘制子集1的Q-Q图
qqline(mydata1$TCHO)  #增加趋势线
qqnorm(mydata2$TCHO, ylab="X", main="Diabetes")  #绘制子集2的Q-Q图
qqline(mydata2$TCHO)  #增加趋势线

##正态性检验##

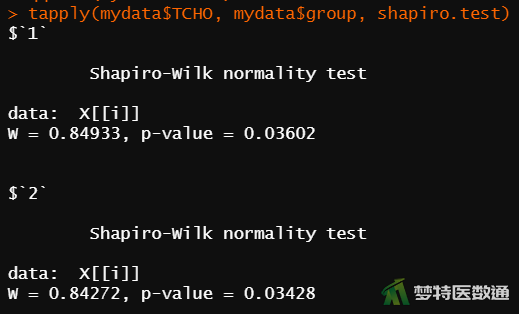
tapply(mydata$TCHO, mydata$group, shapiro.test) #分组进行Shapiro-Wilk正态性检验

(2) 结果解读

图3“summary (描述性分析)”命令运行结果，列出了观察变量的“Min.(最小值)”、“1^st Qu.(P25)”、“Median(中位数)、“Mean(平均值)”、“3^rd Qu.(P75)”和“Max.(最大值)；图4“is.na(缺失值)”运行结果显示该数据不存在缺失值。

图5中的Q-Q图上两组散点偏离对角线较远，提示两组数据不服从正态分布；图6的正态性检验结果显示两组的P值为0.03428和0.03602，均＜0.1，也提示两组数据不服从正态分布。关于正态性检验的注意事项详见文章医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现。

2. 条件1判断(方差齐性检验)

(1) 软件操作

##计算标准差##

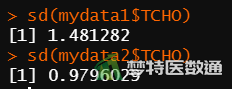
sd(mydata1$TCHO)
sd(mydata2$TCHO)

## levene法方差齐性检验##

mydata$group<-factor(mydata$group,labels = c("Hypertension","Diabetes"))  #把变量group转换为分类变量
library(car)  #调用软件包“car”
leveneTest(TCHO~group,data=mydata,center=mean)  #levene法方差齐性检验

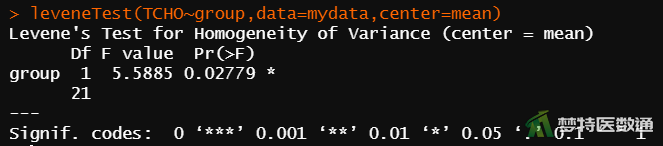
(2) 结果解读

由图7“sd (标准差)”运行结果可知，高血压组和糖尿病组的标准差分别为1.48和0.98，两组之间标准差数值貌似存在差异，但还需要依据统计学检验的结果进行判断。

图8“Homogeneity of Variances Test (Levene’s) (Levene’s方差齐性检验)”为方差齐性检验结果，可见F=5.5885，P=0.02779＜0.1，提示两组数据方差不齐。关于方差齐性检验的更多内容请阅读医学统计学核心概念及重要假设检验的软件实现(4/4)——方差齐性检验及SPSS实现。

综上，本案例中两组连续变量数据既不服从正态分布，也不满足方差齐性，可以考虑使用Wilcoxon秩和检验。

 (三) 统计描述及推断

1. 软件操作

## Wilcoxon秩和检验##

wilcox.test(TCHO ~ group, data = mydata, alternative = "two.sided") #对比两组数据的排序是否相同

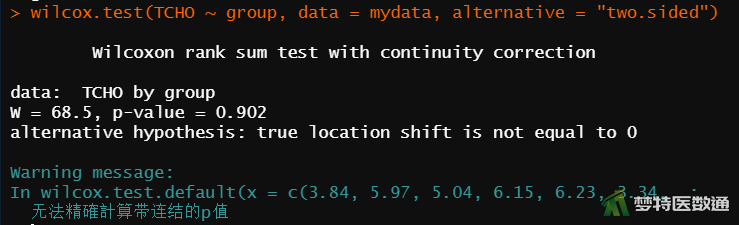
2. 结果解读

本案例采用Wilcoxon秩和检验的分析结果，由图9检验结果可知，W = 68.5, P = 0.902，差异无统计学意义(P>0.05)，尚不能认为高血压患者和糖尿病患者的血清总胆固醇含量不同。

四、结论

本研究采用Wilcoxon秩和检验检验判断高血压患者和糖尿病患者的血清总胆固醇含量是否不同。通过Q-Q图和Shapiro-Wilk检验，提示两组数据不服从正态分布；通过Levene’s检验，提示两组数据总体方差不齐，符合使用Wilcoxon秩和检验的条件。

结果显示，高血压患者和糖尿病患者的TCHO含量分别为6.060 (P₂₅~P₇₅：3.790~6.540) mmol/L和5.040 (P₂₅~P₇₅：4.825~5.430) mmol/L。Wilcoxon秩和检验结果显示，两组人群TCHO含量差异无统计学意义(W=68.5，P=0.902)，差异无统计学意义(P>0.05)。因此，尚不能认为高血压患者和糖尿病患者的血清总胆固醇含量不同。