配对卡方检验(Paired χ² Test)——SAS软件实现

关键词：SAS; 配对四格表; 配对卡方检验; McNemar检验

一、案例介绍

某实验室分别用A方法和B方法对600名患者血清中某抗体进行测定，问两种方法的检测结果有无差别？

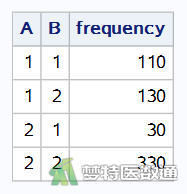
创建变量“A”和“B”分别代表两种测定方法。赋值“1”和“2”分别代表抗体检测阳性和阴性。创建频数变量“Frequency”，代表对应检测方法和检测结果下的对子数。数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较两种方法的检测结果有无差别，属于配对设计，可以认为是在比较两种方法检测结果的一致性，或者比较两者阳性检测率的差异。每个数字代表的是一个对子，而不是单独的一个频数。对于本案例可采用2×2配对χ²检验(McNemar test)进行分析。但需要满足3个条件：

条件1：观察变量为二分类变量，本案例数据为检测方法的阴性和阳性，满足该条件。

条件2：试验方法或干预措施为两个，本案例为A和B两种检测方法，满足该条件。

条件3：研究设计为配对设计，即对同一批样本或研究对象进行两种方法的检测或干预。本案例对同一组患者使用两种抗体检测方法，为配对设计，满足该条件。

三、软件操作及结果解读

(一) 适用条件判断

根据研究设计，本案例数据满足条件1—条件3。

(二) 统计描述及推断

1. 软件操作

本案例为频数资料，需要先手动输入数据。

data mydata;
input A B frequency@@;
cards;
1 1 110 1 2 130 2 1 30 2 2 330
;
proc print noobs;run;

结果如图1所示。

其次进行卡方检验，通过weight对frequency进行加权处理。

proc freq data=mydata;
weight frequency;
tables A*B/ agree;
exact mcnem;/*展示精确慨率法*/
run;

2. 结果解读

(1) 统计描述

图2为“A方法*B方法Crosstabulation(A方法*B方法交叉表)”，给出了A、B两种方法检测一致的对子数和不一致的对子数，各自检测的阳/阴性频数和百分比。可知两种检验方法一致的有440对(同为阳性110对，同为阴性330对)，不一致的有160对(A方法为阳性，B方法为阴性130对；A方法阴性，B方法阳性30对)。

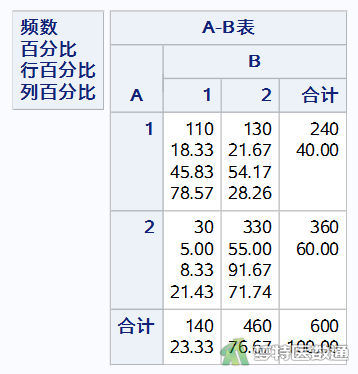
(2) 统计学推断

由于本案例b+c=160≥40，所以k可使用配对χ²检验的结果。图3中“Chi-Square Tests(卡方检验)”给出了McNemar检验结果，可知P<0.0001，提示两种方法检出的阳性率差异有统计学意义，即两种检测方法结果不同。

data mydata;
	 input a b c d;
	 if b+c lt 40 then chisq=(abs(b-c)-1)**2/(b+c);
	 else chisq=abs(b-c)**2/(b+c);
	 p=1-probchi(chisq,1);
	 if p lt 0.0001 then p1="<0.0001";
	 cards;
	 110 130 30 330
	 ;
proc print;run;

结果如图4

其中a，b，c，d分别代表四个格子的频数(该过程仅作展示)：

四、结论

本研究采用2×2 配对χ²检验(Paired Samples McNemar Tests)评价A方法和B方法检测患者血清中某抗体阳性率的一致性。结果显示检测不一致的有160对(A方法为阳性，B方法为阴性130对；A方法阴性，B方法阳性30对)；配对χ²检验分析发现，两种检测方法结果不同(P<0.0001)。

五、知识小贴士

(一) 适用情形

临床研究中常见的需要使用配对卡方检验的设计包括：

• 一组研究对象干预前后的配对，如一组高血压患者使用降压药前后血压达标率的比较。
• 一组研究对象身体不同部位的配对，如两种治疗某皮肤病的药物分别用在同一组研究对象的左臂和右臂，进行疗效的比较。
• 条件配对，如在同一窝老鼠中选择性别和体重相同的2只作为一个对子，组成多个对子；再将每个对子中的2只老鼠随机分配到2个处理组中去，然后比较两种处理方法的效果。
• 同一批生物样本不同检测方法的配对，如同一批血液样本被分成2份，分别用两种方法检测HbsAg (乙肝表面抗原)。

(二) 方法选择

• 对于2×2配对四格表，定义四个格子分别为a、b、c和d，a、d为结果一致的对子数，b和c为结果不一致的对子数。需要根据b+c的大小，选择分析方法：当b+c≥40时，选择McNemar检验(2×2配对χ²检验)；当20≤b+c<40时，选择校正McNemar检验；当b+c<20时，选择确切概率法(如图3中的Pr >= 精确卡方)。
• SAS中不主动进行校正McNemar检验，需手动编程。
• 校正McNemar程序举例

data mydata;
	 input a b c d;
	 if b+c lt 40 then chisq=(abs(b-c)-1)**2/(b+c);
	 else chisq=abs(b-c)**2/(b+c);
	 p=1-probchi(chisq,1);
	 if p lt 0.0001 then p1="<0.0001";
	 cards;
	 110 130 30 330
	 ;
proc print;run;

结果如图4

其中a,b,c,d分别代表四个格子的频数(该过程仅作展示)：