分层卡方检验(CMH χ² Test)——SAS软件实现

关键词：SAS; 卡方检验; 分层卡方检验; CMH检验; Cochran-Mantel-Haenszel检验

一、案例介绍

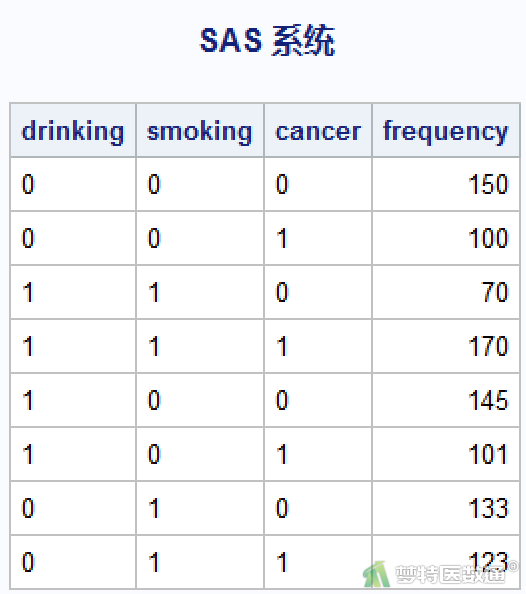
某医学组织研究饮酒是否会提高患肝癌风险,考虑到吸烟会严重影响饮酒和患癌风险间的相关性，因此将吸烟作为混杂因素处理，设计了一项病例对照研究。数据中混杂因素为smoking，标签为“吸烟”，测量尺度为“名义”，赋值为0=否(不吸烟)、1=是(吸烟)。分组变量为drinking，标签为“饮酒”，测量尺度为“名义”，赋值为0=否(不饮酒)、1=是(饮酒)。变量cancer，标签为“是否患癌”，测量尺度为“名义”，赋值为0=否、1=是。频数变量frequency，标签为“频数”，测量尺度为“标度”，记录不同组的例数。数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析

本案例的分析目的是研究饮酒是否会提高患肝癌风险，吸烟作为混杂因素。即比较不同吸烟情况下饮酒组与不饮酒组患癌率是否有差异。针对这种情况可以制作四格表，并进行分层卡方检验。但需要满足3个条件：

条件1：分组变量与观察变量均为二分类变量。本案例的分组变量和观察变量均为二分类变量，该条件满足。

条件2：观察变量相互独立。本研究中各研究对象的观察变量都是独立的，不存在互相干扰的情况，该条件满足。

条件3：各层内总数及最小期望频数满足卡方检验相应条件(χ²检验的注意事项——使用技巧)。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

对于本案例数据，条件1和条件2均满足。但需要通过总例数和期望频数来选择具体的分析方法(Pearson卡方检验、连续校正卡方检验或Fisher确切概率法)。这一判断过程通过统计描述来完成，详见下文。

(二) 统计描述及推断

1. 软件操作

本案例为频数资料，首先，需要先手动输入数据。

data Risk;
input drinking $ smoking $ cancer $ frequency @@;
datalines;
0 0 0 150
0 0 1 100
1 1 0 70
1 1 1 170
1 0 0 145
1 0 1 101
0 1 0 133
0 1 1 123
;
proc print noobs;
run;

结果见图2。

其次，进行卡方检验，通过weight对frequency进行加权处理。

proc freq data = Risk;
weight frequency;
tables cancer*drinking/chisq expected;
exact pchi or;
run;
proc freq data = Risk;
weight frequency;
tables smoking*cancer*drinking/chisq expected;
exact pchi or;
run;

最后，进行分层卡方检验。

proc freq data = Risk;
weight frequency;
tables smoking*cancer*drinking/cmh nopercent norow nocol;
run;

2. 结果解读

(1) 统计学描述

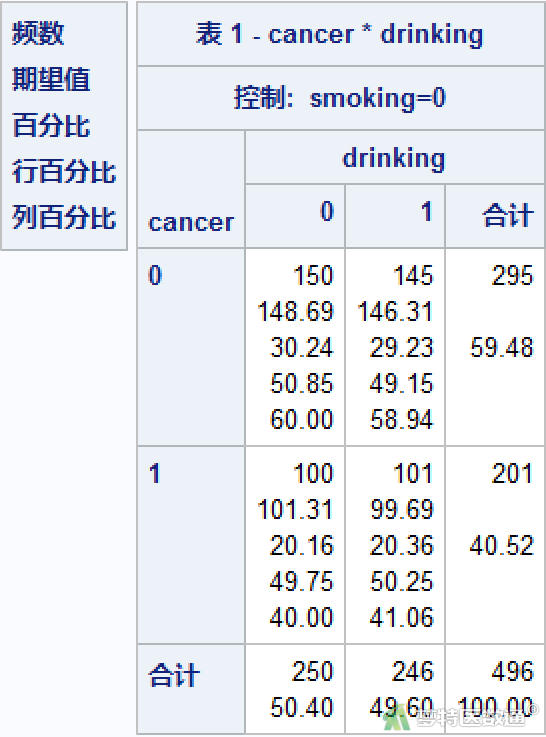
“是否患病*饮酒*吸烟交叉表”见图3、4，其给出了混杂因素(吸烟)分层下，饮酒组和未饮酒组的观察值、期望频数及组内占比。可知整体检验总例数为992例，各层的最小期望频数>5；分层检验时，各层的总例数均为496例，最小期望频数均>5，因此整体检验和分层检验均可使用Pearson卡方检验分析结果。由各层的描述性分析结果可知，吸烟组患癌者中饮酒的比例为58.02%，而不吸烟组患癌者中饮酒的比例仅为50.25%，提示在不同吸烟情况的两组人群中饮酒比例存在一定差异。但是这种差异是否会造成两组人群中饮酒与患癌关联的不一致，需要依据各层卡方检验和CMH检验的结果进行判断。

(2) 统计学推断

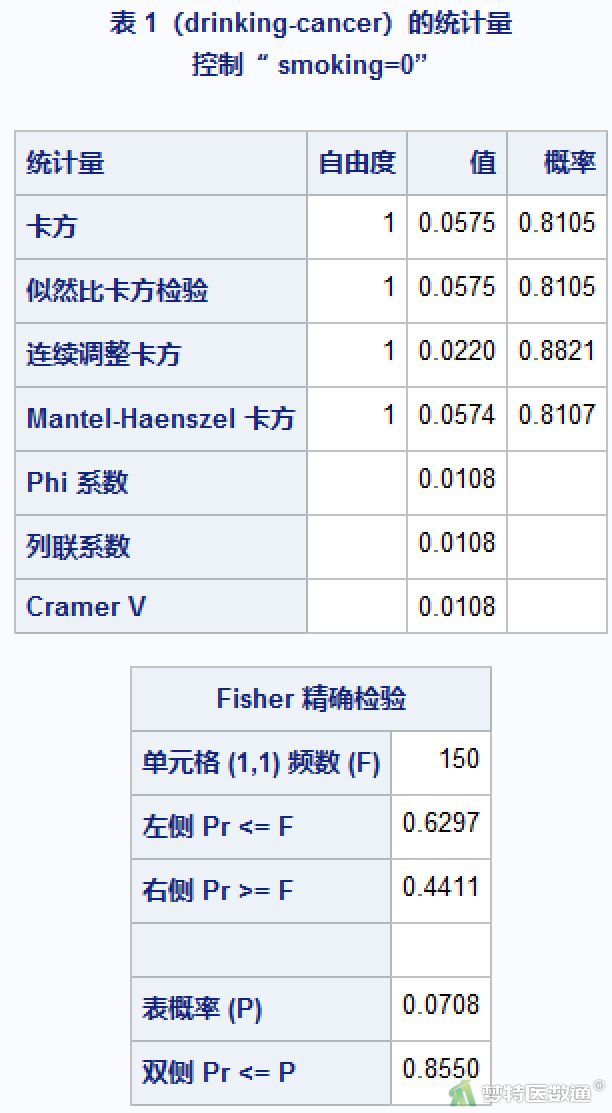
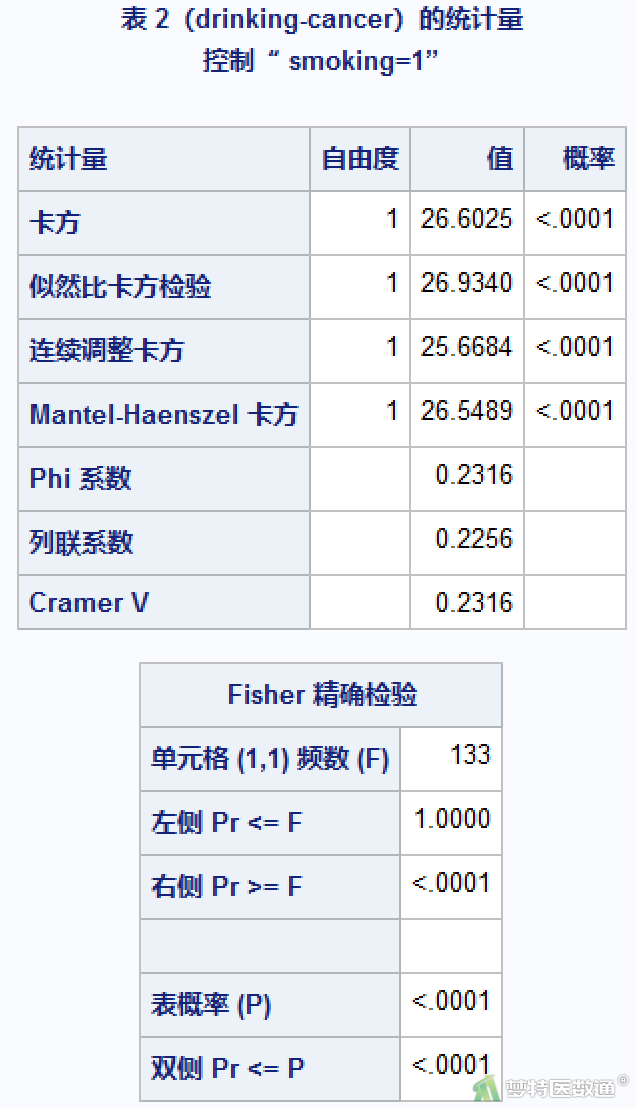
本案例卡方检验结果见图5、图6、图7。其分别列出了吸烟组和不吸烟组的卡方检验结果。“风险评估”结果见图8、图9，列出了各组的暴露风险比值比(OR值)。

若不考虑混杂因素(吸烟)，总计分析χ²=13.5514，P＜0.001，OR=1.600(95%CI 1.245~2.055)，说明患癌和饮酒间存在相关性。吸烟人群中，χ²=26.603，P<0.001，OR=2.626 (95%CI 1.812~3.805)，说明患癌和饮酒间的相关性有统计学意义。而不吸烟人群中，结论与此相反，χ²=0.057，P< 0.811，OR=1.045 (95%CI 0.730~1.495)，说明患癌和饮酒间的相关性无统计学意义。对比吸烟组和不吸烟组的分析结果可知，混杂因素(吸烟)的确会对饮酒与患癌之间的关联产生影响。

“比值比齐性检验”结果见图10，即对不同分层下OR值是否一致进行检验，也称为OR值同质性检验。通常情况下，若“比值比齐性检验”结果呈显著性(P<0.05)，则说明有混杂因素，需要考虑分层项(混杂因素)，报告不同分层项下的数据分析结果；反之若P≥0.05，则说明没有混杂因素，不需要考虑分层项，报告整体的结果即可。

检验结果显示，Breslow-Day法 χ²=12.322，P<0.001，说明按照是否吸烟分层后，层间的OR值存在着一定的异质性。

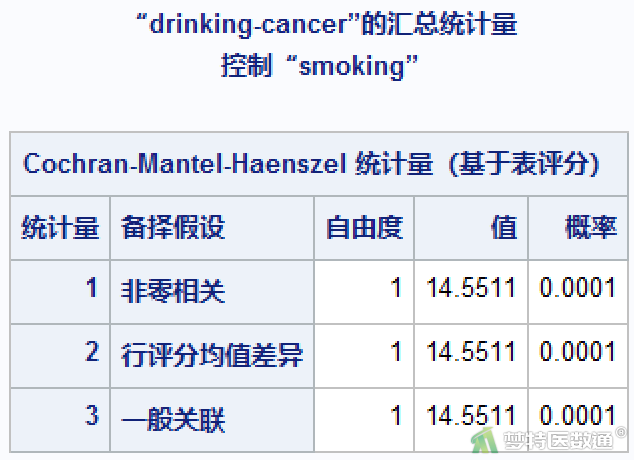
“条件独立性检验”结果，即分层卡方检验的结果见图11。在控制分层变量后总的检验Cochran-Mantel-Haenszel的统计结果。由于行变量和列变量都是二分类的，故可以看作双向无序资料。3种结果是一致的，结果为χ²=14.5511，P= 0.0001，说明考虑了吸烟的影响后，患癌与饮酒之间的相关性确实有统计学意义。

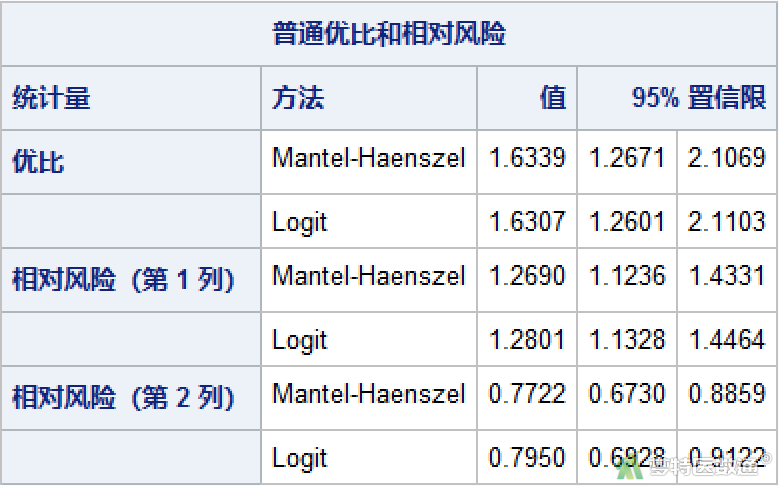
估计的合并OR值，即在比值比齐性检验结果认为各层OR值同质的前提下，进一步去估算其合并的关联强度，结果见图12。

本例结果显示，在控制了“吸烟”分层因素的影响后，饮酒对患癌的风险是危险因素，其合并OR=1.634，95%CI为1.267~2.107，“渐进显著性(双侧)”P＜0.001，说明OR值有统计学显著性。

但需要注意的是，本例中，比值比齐性检验的结果显示层间OR值存在一定异质性，因此不宜合并OR值，建议分层报告结果；若层间OR值一致，则可报告最后合并的OR值。

四、结论

本研究分析不同吸烟情况下饮酒与患肝癌的关联，采用分层卡方检验。比值比齐性检验结果显示P<0.05，提示层间的OR值具有异质性，此时不宜计算合并OR值。按照是否吸烟进行分层，在吸烟人群中，饮酒和患癌的相关性具有统计学意义，OR值为2.626 (95%CI为1.812~3.805)，χ²=26.603，P<0.001。而在不吸烟人群中，饮酒和患癌的相关性无统计学意义，OR值为1.045 (95%CI为0.730~1.495)，χ²=0.058，P=0.811。