行×列表资料的χ²检验用于多个样本率的比较、两个或多个构成化的比较以及双向无序分类资料的关联性检验。其基本数据有以下3种情况:①多个样本率比时,有R行2列称为R×2表;②两个样本的构成比比较时,有2行C列,称2×C表;③多个样本的构成比比较以及双向无序分类资料关联性检验时,有R行C列,称为R×C表。以上3种情况可统称为行×列表资料。本篇文章将介绍行×列表资料的χ²检验之多个样本率或构成比比较的适用条件及假设检验。
关键词:列联表卡方检验; 多个率比较; 关联性检验; 列联系数
一、适用条件
条件1:分组变量和观察变量均为分类变量,至少有一个无序多分类变量,且观察变量不是有序多分类变量。
条件2:观测值之间相互独立。
条件3:样本量足够大,使得任一单元格内的期望频数均≥5。
条件4:两个变量是同一随机样本的两种属性。
二、统计量计算
(一) 多个样本率及样本构成比的比较
行×列表资料的χ²检验仍用Pearson χ²公式,即公式 \( \chi^{2}=\sum \frac{(A-T)^{2}}{T} \) 计算检验统计量χ²。因该式需先计算理论频数TRC,计算较烦琐,可将计算理论数的公式 \(T_{RC}=\frac{n_{R} n_{C}}{n}\) 代入公式 \( \chi^{2}=\sum \frac{(A-T)^{2}}{T} \) ,化简后得行×列表资料χ²检验的专用公式为:
\( \chi^{2}=n\left(\sum \frac{A^{2}}{n_{R} n_{C}}-1\right), v=(\text { 行数 }-1)(\text { 列数 }-1) \)式中A为实际频数,nR为相应行的合计,nC为相应列的合计,n为总例数。
(二) 双向无序分类资料的关联性检验
对于两个分类变量皆为无序分类变量的行×列表资料,又称为双向无序 R×C 表资料。若是一个样本的双向无序 R×C 表资料,研究者常分析两个分类变量之间有无关系,关系的密切程度如何,此时可用行×列表资料χ²检验来推断两个分类变量之间有无关系(或关联)。
1. 检验统计量χ²值的计算
与(一)中计算检验统计量χ²的方法相同。
2. 列联系数C值的计算
若推断出两个分类变量有关系,可进一步分析关系的密切程度,此时可计算 Pearson 列联系数 C :
\( C=\sqrt{\frac{\chi^2}{n+\chi^2}} \)式中χ²为行×列表资料的χ²值, n 为样本含量。列联系数 C 取值范围在0~1之间。0表示完全独立;1表示完全相关;愈接近于0,关系愈不密切;愈接近于1,关系愈密切。
三、案例数据
某科室回顾性研究推拿疗法、药物疗法和针灸疗法3种疗法治疗腱鞘炎的疗效,数据见图1。问3种疗法的有效率有无差别以及疗法与效果的关联(分为有效和无效)?
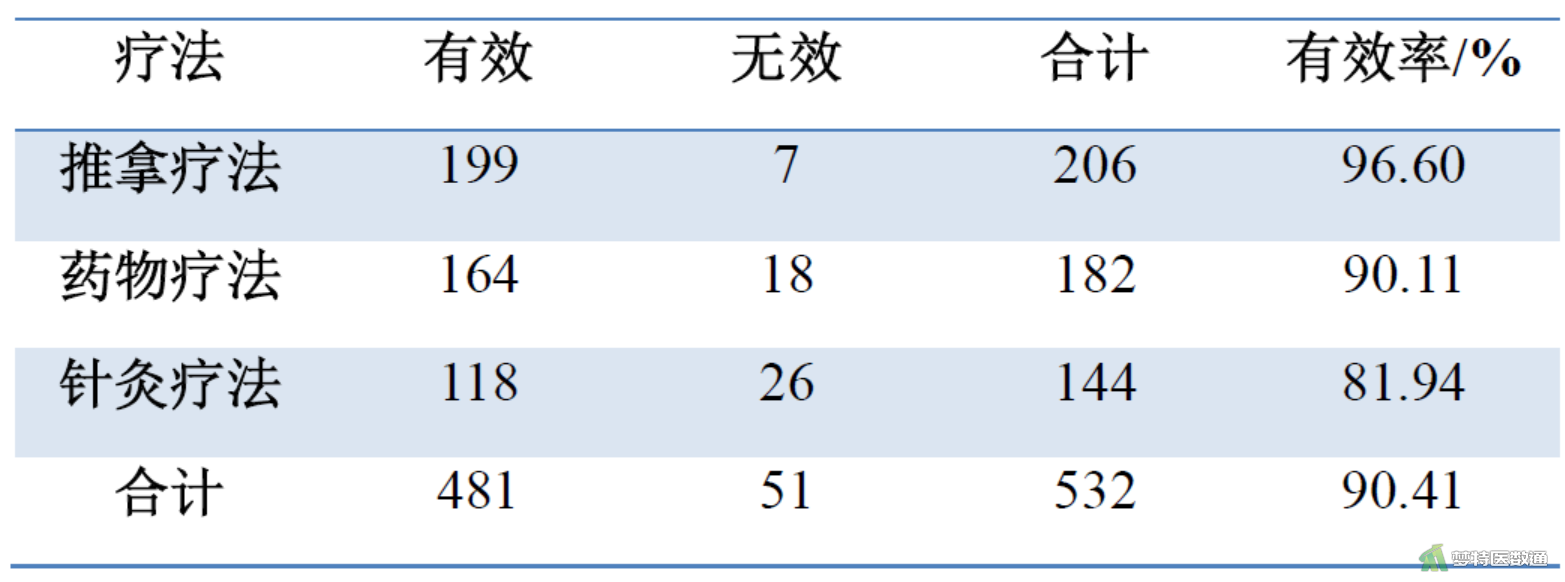
四、有效率比较的假设检验
本案例属于多个样本率比较或双向无序分类资料的关联性检验,先进行有效率比较的假设检验。
(一) 建立检验假设,确定检验水准
H0:π1=π2=π3,即3种疗法治疗腱鞘炎的总体有效率相等
H1:3种疗法治疗腱鞘炎的总体有效率不全相等
α=0.05
(二) 计算检验统计量
\( \chi^{2}=n\left(\sum \frac{A^{2}}{n_{R} n_{C}}-1\right)=532\left(\frac{199^{2}}{206 \times 481}+\frac{7^{2}}{206 \times 51}+\cdots+\frac{26^{2}}{144 \times 511}-1\right)=21.038 \)v=(行数-1)(列数-1)=(3-1)(2-1)=2
(三) 确定P值,作出推断结论
按v=2查(χ²界值表),因21.038> \( \chi_{0.005}^{2}=10.60 \) ,故P<0.005。按α=0.05水准,拒绝H0,接受H1,可认为3种疗法治疗腱鞘炎的总体有效率不全相等。
五、关联性检验
因为可认为疗法和效果之间有关联,可进一步计算 Pearson 列联系数,以分析其关系密切程度。
(一) 建立检验假设,确定检验水准
H0:疗法与效果之间无关联
H1:疗法与效果之间有关联
α=0.05
(二) 计算检验统计量
\( \text { 列联系数 } C=\sqrt{\frac{\chi^{2}}{n+\chi^{2}}}=\sqrt{\frac{21.038}{532+21.038}}=0.1950405 \)(三) 作出推断结论
由列联系数C=0.1950405可知,疗法与效果之间虽有关联性,但关联性较弱。