独立样本Wilcoxon秩和检验：Mann-Whitney U检验（Mann-Whitney U Test）——SPSS软件实现

关键词：SPSS; 非参数检验; 秩和检验; Wilcoxon秩和检验; 独立样本秩和检验; Mann-Whitney U检验

一、案例介绍

某医师对12例高血压患者和11例糖尿病患者血清总胆固醇(TCHO)含量(mmol/L)进行了测定，问高血压患者和糖尿病患者的血清总胆固醇含量是否不同？

创建代表组别的数值型变量“group(组别)”，赋值为“1”或“2”分别代表高血压患者和糖尿病患者，变量测量尺度设为“名义”。创建记录血清总胆固醇(TCHO)的数字型变量，测量尺度设为“标度”。部分数据见图1。案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较两组计量资料是否有差异，即判断高血压患者和糖尿病患者的血清总胆固醇含量是否不同。针对这种情况可以使用Mann-Whitney U检验。比较两组计量资料是否有差异可以使用两独立样本t检验或Mann-Whitney U检验。如果数据满足正态性和方差齐性要求则可以使用两独立样本t检验。若满足正态性，不满足方差齐性，可使用校正t检验(Welch’s t检验)。但如果数据的方差相差太大，最好使用非参数检验(Mann-Whitney U检验)。如果数据正态性和方差齐性都不满足，最好使用非参数检验(Mann-Whitney U检验)。Mann-Whitney U检验，需要满足3个条件：

条件1：有一个观察变量，且观察变量为连续变量(不满足正态分布或方差严重不齐)或等级变量。该条件需要通过软件判断或专业判断。

条件2：有一个分组变量，且为二分类。本研究中分为高血压患组和糖尿病组，该条件满足。

条件3：具有相互独立的观测值。本研究中各研究对象的TCHO含量都是独立的，不存在互相干扰的情况，该条件满足。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件1判断(正态性检验)

(1) 软件操作

① 选择“分析”—“描述统计”—“探索”(图2)。

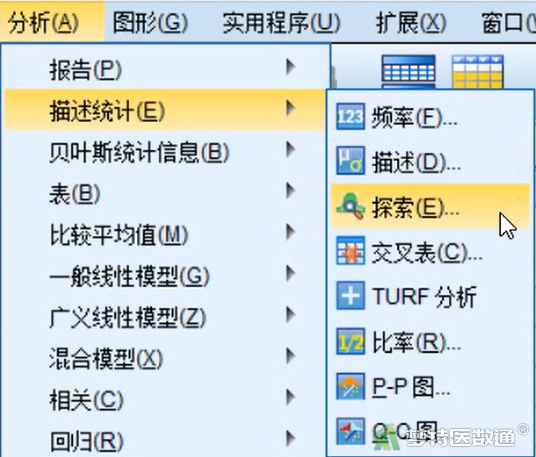
② 在“探索”对话框中将观察变量“TCHO”选入右侧“因变量列表”框，将分组变量“group”选入右侧“因子列表”(图3)。

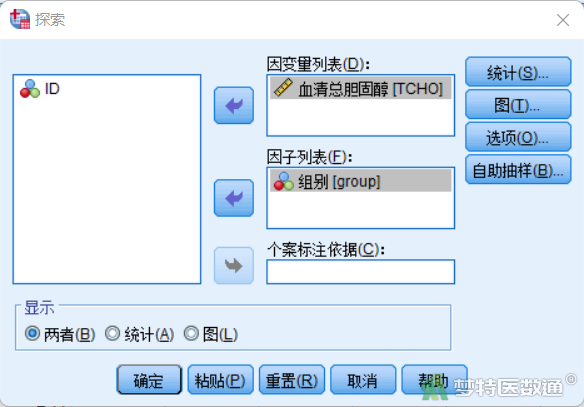
③ 在“图”子对话框中勾选“含检验的正态图”，取消勾选“茎叶图”，其他不变，如图4所示，点击“继续”，回到“探索”对话框，点击“确定”，即可得到正态性检验结果。

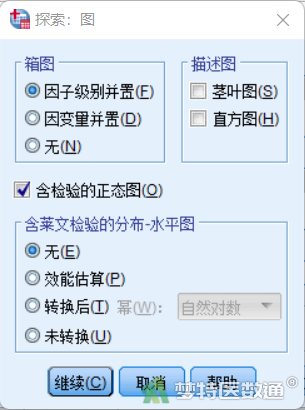
(2) 结果解读

图5是对两组数据的“描述”结果，包括变量“TCHO”的“平均值”、“95%置信区间”、“中位数”、“标准偏差”、“四分位距”等指标。可知高血压组和糖尿病组患者的TCHO中位数(四分位距)分别为6.06 (2.99) mmol/L和5.04 (0.78) mmol/L。

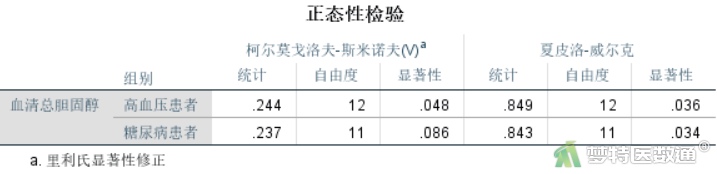
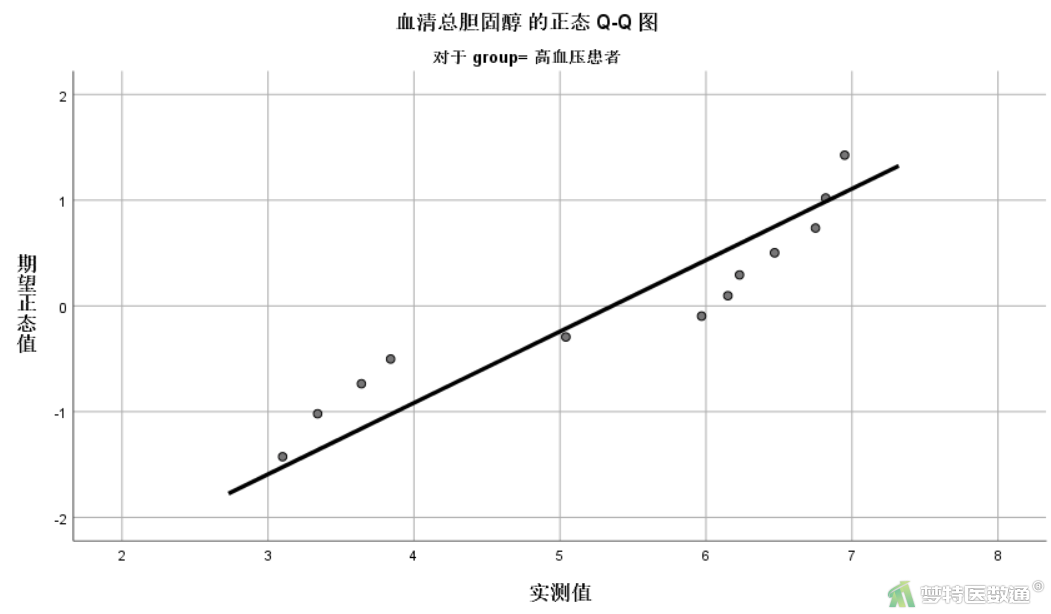
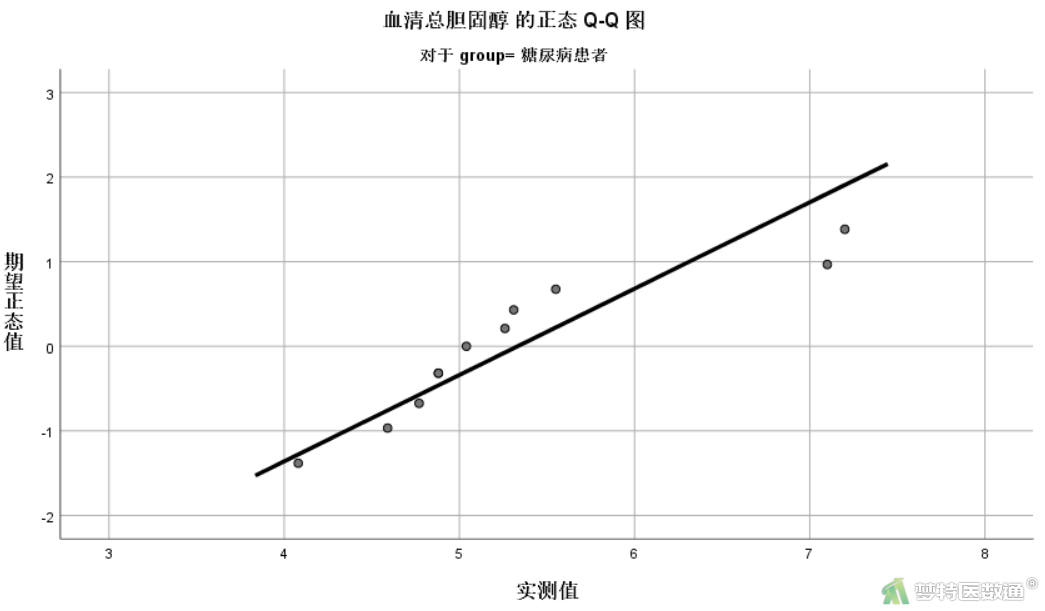
图6显示了两种正态性检验的结果，柯尔莫哥洛夫-斯米诺夫，K-S检验和夏皮罗-威尔克正态性，S-W检验。K-S检验适用于大样本资料，本案查看S-W检验结果，两组P值分别为0.036和0.034，均<0.1，提示两组数据均不服从正态分布。图7-1和图7-2分别是组1和组2数据的Q-Q图，两组散点偏离对角线较远，也提示两组数据不服从正态分布。关于正态性检验的注意事项详见文章(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。

2. 条件1判断(方差齐性检验)

(1) 软件操作

① 选择“分析”—“比较平均值”—“单因素ANOVA检验” (图8)。

② 在“单因素ANOVA检验”对话框中将变量“TCHO”选入右侧“因变量列表”框，将变量“group”选入右侧“因子”框(图9)。

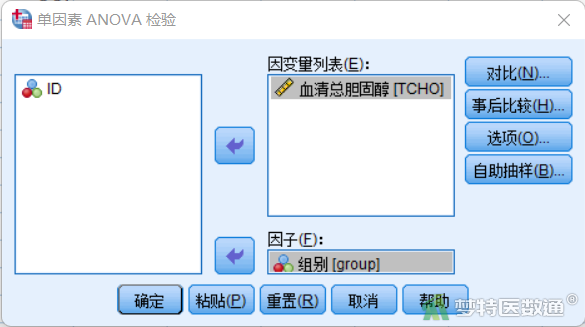
③ 在“选项”对话框中勾选“描述”和“方差齐性检验”后点击“继续”(图10)，回到“单因素ANOVA检验”对话框后点击“确定”，则得到方差齐性检验结果。

(2) 结果解读

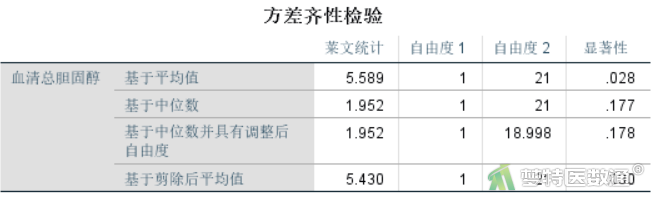
图11是“方差齐性检验”结果，可知“基于平均值的莱文统计” F=5.589，P=0.028<0.1，提示两组数据方差不齐，不满足条件2。关于方差齐性检验的更多内容请阅读(医学统计学核心概念及重要假设检验的软件实现(4/4)——方差齐性检验及SPSS实现)。

综上，本案例中两组连续变量数据既不服从正态分布，也不满足方差齐性，可以考虑使用Mann-Whitney U检验。

(二) 统计描述及推断

1. 软件操作

① 选择“分析”—“非参数检验”—“旧对话框”—“2个独立样本”(图12)。

② 在“双独立样本检验”对话框中,将变量“TCHO”选入右侧“检验变量列表”框，将变量“group”选入右侧“分组变量”框(图13)。

③在“双独立样本检验”对话框中点击“定义组”后出现“双独立样本：定义组”子对话框，在该对话框中输入要比较的两组数据的组别名称。本案例在“组1”处输入“1”，“组2”处输入“2”，然后点击“继续”(图14)，回到“双独立样本检验”对话框；“检验类型”默认为“曼-惠特尼”后点击“确定”，则得到统计描述及推断的结果。

2. 结果解读

(1) 统计描述

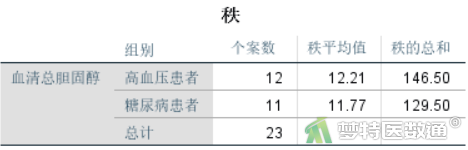
Mann-Whitney U检验是将原始数据排序后分配秩次进行的假设检验，所以图15“秩”是对两组变量秩次的统计描述。可见高血压组和糖尿病组“个案数”分别为12和11，“秩平均值”分别为12.21和11.77。从上述正态性检验结果中可知，高血压组和糖尿病组的中位数(四分位距)分别为6.06 (2.99) mmol/L和5.04 (0.78) mmol/L。两组数值较为接近，提示TCHO含量可能不存在差异，但还需要依据统计学检验的结果进行判断。

(2) 统计学推断

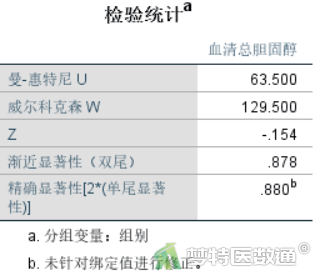
图16是检验结果，其中“曼-惠特尼 U”表示统计量U=63.500，渐进显著性(双尾)代表双侧检验的渐进P值，精确显著性[2*(单尾显著性)]代表精确P值。样本量越大，渐进P值就会越接近真实P值。如果每组样本量均小于20，SPSS会自动计算精确P值，此时以精确P值进行假设检验的判断。如果每组样本量均大于20，渐进P值可以较好的代表真正的P值，此时可以选择渐进P值进行假设检验的判断。本案例中两组样本量均小于20，查看精确P值=0.880>0.05，所以尚不能认为高血压患者和糖尿病患者的TCHO含量不同。

四、结论

本研究采用Mann-Whitney U检验判断高血压患者和糖尿病患者的TCHO含量是否不同。通过Q-Q图和Shapiro-Wilk检验，提示两组数据不服从正态分布；通过Levene’s检验，提示两组数据总体方差不齐，符合使用Mann-Whitney U检验的条件。

结果显示，高血压患者和糖尿病患者TCHO中位数分别为6.06 (2.99) mmol/L和5.04 (0.78) mmol/L，平均秩次分别为12.21和11.77。Mann-Whitney U检验结果显示，两组人群TCHO含量差异无统计学意义(U=63.500，P=0.880>0.05)。因此，尚不能认为高血压患者和糖尿病患者的血清总胆固醇含量不同。