在前面文章中我们介绍了简单线性回归分析(Simple Linear Regression Analysis)的假设检验理论,本篇文章将实例演示在SAS软件中实现简单线性回归分析的操作步骤。
关键词:SAS; 简单线性回归; 直线回归; 残差齐性检验; 残差正态检验; 哑变量设置
一、案例介绍
研究健康成年人的体重和双肾脏总体积(ml)的关系,测得24名健康成年人的体重wt (kg)与双肾脏总体积volume (ml),拟探讨健康成年人的体重与双肾总体积是否有关,并希望通过健康成年人的体重预测双肾总体积。部分数据见图1。本文案例可从“附件下载”处下载。其中,ID表示受试者的序号,wt表示体重,volume表示双肾脏总体积。
二、问题分析
本案例的分析目的是通过判断两个计量资料之间的关系,同时使用其中一个变量预测另一个变量,计算其中一个变量对另一个变量变异的解释程度。针对这种情况,可以使用简单线性回归分析。但需要满足6个条件:
条件1:因变量为连续变量。本研究中,双肾总体积为连续变量,该条件满足。
条件2:若自变量是连续变量,则与因变量之间存在线性关系。该条件需要通过软件分析后判断。
条件3:各观测值之间相互独立,即残差之间不存在自相关。通过研究设计和数据收集的过程分析,可判断本案例中观测值之间不存在互相影响的情况。该条件还可通过Durbin–Watson检验辅助判断。
条件4:自变量不存在显著的异常值,该条件可以通过Cook距离(Cook’s D)判断。
条件5:残差符合正态(或近似正态)分布,该条件需要通过软件分析后判断。
条件6:残差方差齐。该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 适用条件判断
1. 条件3判断(线性关系判断)
(1) SAS实现
首先导入数据,代码如下:
proc import datafile="D:\简单线形回归---SAS软件实现\简单线性回归分析.csv" dbms=csv out=data1 ; run;
使用如下的sgplot过程步绘制体重和双肾脏总体积的散点图:
proc sgplot data=data1; scatter x=wt y=volume; run;
(2) 结果解读
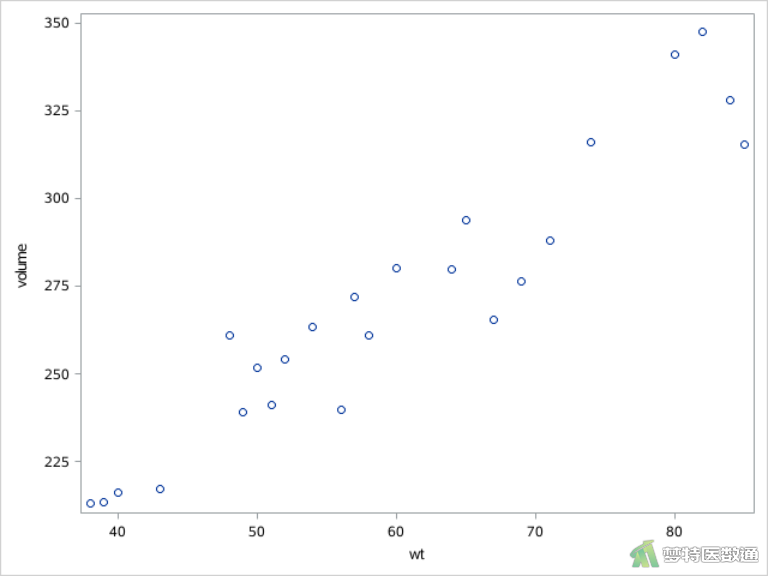
由图2可见,散点大致呈一条直线,提示体重和双肾脏总体积存在线性关系,满足条件3。
2. 条件3判断(独立性判断)
(1) SAS实现
SAS的reg过程步实现线形回归,model语句等号左边是因变量,等号右边是自变量,其中model语句的DW选项可以输出Durbin–Watson自相关检验的结果,代码如下:
proc reg data=data1; model volume=wt/DWPROB; run;
(2) 结果解读
Durbin–Watson检验的结果如图3所示,统计量为2.078,Pr<DW=0.5794且Pr>DW=0.4206,说明正相关和负相关检验均无统计学意义,则体重和双肾脏总体积相互独立,因此,本研究数据满足条件3。

3. 条件4判断(异常值检测)
通过图2的散点图可见,数据不存在异常值。但仍需要统计分析结果的判断。
(1) SAS实现
SASreg过程步, model语句的r选项输出残差信息,其中包括Cook’s D(库克距离)的值,代码如下:
proc reg data=data1; model volume=wt/r; run;
(2) 结果解读
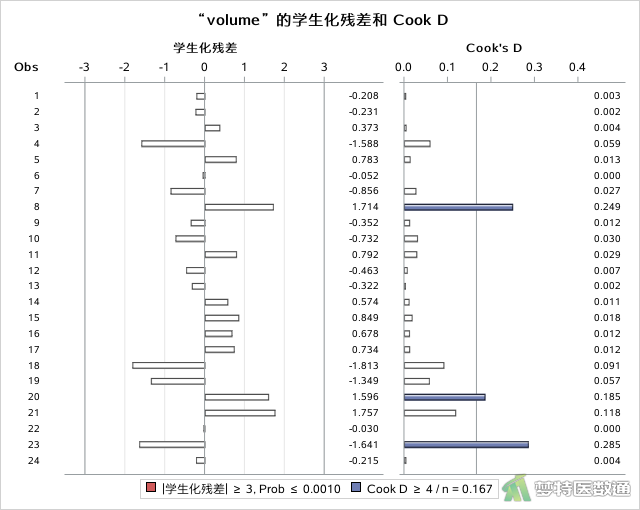
如图4所示,本案例所有观测数据的Cook’s D值均<0.5,提示不存在显著异常值,本研究数据满足条件4。
4. 条件5判断(残差的正态性检验)
(1) SAS实现
正态性检验可以通过残差图来观察,SAS9.3以后的版本在执行proc reg过程步时会自动输出残差图,无须加任何选项。也可以对残差进行正态性检验,SAS操作代码如下:
proc reg data=data1; model volume=wt; output out=res r=r; run; proc univariate data=res normal; var r; run;
其中reg过程步中的output语句是将残差值输出到res数据集,残差用变量r表示;
使用univariate过程步对残差进行正态性检验。
(2) 结果解读
从图5所示的残差图可见,残差基本以0为中心上下波动,而且并未出现有方差增大或减少的趋势,直观上可以认为符合正态分布。
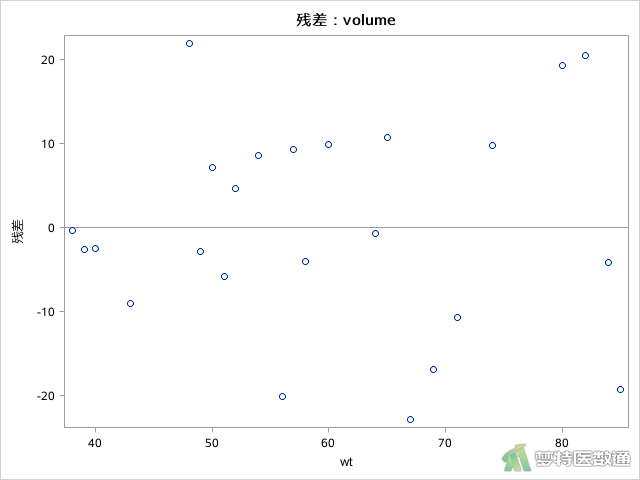
图6展示了正态性检验的结果,Shapiro-Wilk检验统计量W=0.963195,P=0.5059,表明残差服从正态分布,满足条件5。
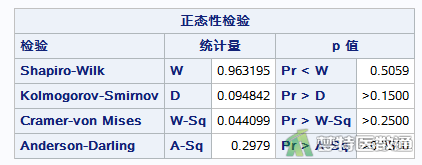
5. 条件6判断(残差的方差齐性检验)
(1) SAS实现
reg过程步model语句的spec选项执行方差齐性的White检验,代码如下:
proc reg data=data1; model volume=wt/spec; run;
(2) 结果解读
如图7所示,方差齐性检验结果显示,不能拒绝“等方差齐性”的原假设(P=0.1058),提示残差的方差齐,本研究数据满足条件6。

(二) 模型拟合
1. SAS实现
线形回归的SAS程序主要通过pro reg过程步实现,如下所示:
proc reg data=data1; model volume=wt/stb clb; run;
其中,stb选项给出标准化回归系数,用来衡量不同自变量对因变量影响的相对重要性;clb选项给出参数估计的95%置信区间。
2. 结果解读
(1) 模型拟合程度
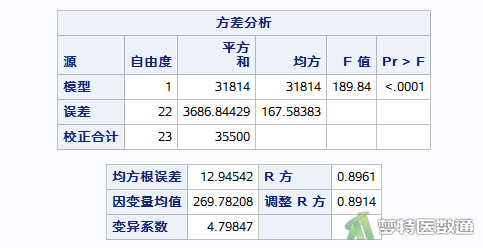
如图8所示,第一部分是方差分析结果,结果表明,模型总体有统计学意义(F=189.84,P<0.0001)。这部分结果是对所有的自变量进行总体的检验,由于该研究只有一个自变量,因此对总体方程的检验结果等同于对该自变量的检验结果。模型的决定系数R2为0.8961,提示自变量(体重)可以解释89.61%的因变量的变异(双肾总体积);校正决定系数adjusted R2为0.8914,提示校正了自变量个数后,自变量(体重)可以解释89.14%的因变量的变异(双肾总体积),该结果表明健康成年人的体重与双肾总体积具有很强的相关性。
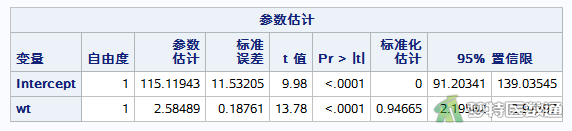
(2) 回归系数解释
图9所示为参数估计结果,展示了截距和自变量的非标准化回归系数及统计量t值及P值,标准化回归系数以及非标准化回归系数的95%CI。结果显示,回归模型的截距为115.119 (95%CI:91.203~139.035),P<0.0001,截距有统计学意义,表明截距≠0,在图2散点图中直观地表现为各散点并非起自零点。体重(wt)的非标准化回归系数为2.585 (95%CI:2.196~2.974),P<0.0001,回归系数有统计学意义,表明斜率≠0,在图2散点图中直观地表现为散点趋势并不平行于横轴,回归系数的数值含义可以解释为,健康成年人体重(wt)每增加1 kg,双肾脏总体积(volume)增加2.585 ml。
据此可以写出本案例的回归方程为:
Volume =115.119+2.585×wt
根据此方程可以计算合理范围内健康成年人体重对应的双肾脏总体积。
四、结论
本研究采用简单线性回归模型通过健康成年人的体重预测双肾总体积。通过绘制散点图,提示两者之间存在线性关系;通过专业判断和Durbin-Watson检验提示数据之前相互独立;通过绘制散点图和库克距离分析,提示数据不存在需要处理的异常值;通过Shapiro-wilk检验及绘制残差图,提示残差服从正态分布;通过White检验,提示残差方差齐。本研究数据满足线性回归分析条件。
线性回归分析方程为:volume = 115.119 + 2.585×wt,回归模型具有统计学意义,F=189.84,P<0.0001;自变量(体重)可以解释89.61%的因变量的变异(双肾总体积),影响程度较高(adjusted R2=0.8914),即体重每增加1 kg,双肾总体积增加2.585 (95%CI:2.196~2.974) ml。
五、分析小技巧
(一) 各观测值之间独立性检验
- 判断观测值是否独立,主要取决于研究设计和数据收集阶段的质量控制,Durbin-Watson检验最好用于辅助判断。Durbin-Watson检验值分布在0~4之间,越接近2,观测值相互独立的可能性越大。
(二) 异常值检测
- Cook’s D(库克距离)用来判断强影响点是否为因变量的异常值点。一般认为当D<0.5时不是异常值点,当D>0.5时认为是异常值点。
- 并非所有的异常点都意味着结果不好,有时候发现异常点可能会提示有更重要的信息。如果出现异常点,首先应检查数据是否录入错误,也可以选择其他相应模型来拟合,或者需要收集更多的数据来证实。
(三) 残差正态性检验
- 如果残差不符合正态分布,可以考虑对因变量进行数据变换,使其服从正态分布后再拟合线形回归模型,也可采用非参数回归。
(四) 残差的方差齐性检验
- 残差的方差齐是指在自变量取值范围内,对于任意自变量取值,因变量都有相同的方差。线形回归中,残差的方差齐实际上要比残差正态分布重要。如果这一条件不满足,可对因变量进行变量变换,使其满足残差方差齐,也可以采用加权回归分析,消除方差的影响。
(五) 回归模型
- 分析中得到的回归截距,是当自变量为0时因变量对应的值。在本研究中,回归截距为当体重为0时,研究对象的双肾总体积为115.119 ml。这显然不符合客观实际,因此无论截距的检验结果是否有统计学意义,一般都不必过多关注,在进行简单线性回归时更多关注的是斜率。
- 在进行回归分析时,要注意避免对数据的过度挖掘,不能将回归模型分析的结果随意延伸到自变量取值范围以外的数值。也不能随意将模型分析结果延伸到因果关系。