简单线性回归分析 (Simple Linear Regression Analysis)——理论介绍

关键词：简单线性回归; 直线回归; 残差齐性检验; 残差正态检验;

一、适用条件

简单线性回归分析，一般适用于以下6个条件：

条件1：因变量和自变量为定量变量。

条件2：因变量和自变量之间具有线性关系，可通过散点图加以判断。

条件3：因变量的观察值来自正态分布且方差相同。

条件4：观察变量不存在显著的异常值。

条件5：观察变量相互独立。

条件6：残差方差齐。

二、直线回归方程

简单线性回归模型(Simple linear regression model)即描述因变量Y如何随自变量X改变而改变，该线性趋势所对应的直线称为回归直线(regression line)，可用以下直线回归方程(linear regression equation)表示：

\(\widehat{Y}=a+b X\)

其中,\(\widehat{Y}\)为X相对应的Y的总体均数的一个样本估计值，称为回归方程的预测值。a是回归直线在Y轴上的截距，表示当X取值为0时相应Y的均数估计值，称为常数项。b是直线斜率，称为回归系数，表示当X变化一个单位时Y的平均改变的估计值。

我们需要找到一条尽可能靠近所有点的直线。将实测值Y与估计值\(\widehat{Y}\)的纵向距离\(\mathrm{Y}-\widehat{\mathrm{Y}}\)称为残差或剩余量(residual)，则问题转化为求最小的残差和。残差的符号有正负，通常取各点残差平方和最小的直线，即“最小二乘(least sum of squares, LS)”原则。数学上易得a、b的计算公式为：

\(a=\bar{Y}-b \bar{X}\)

\(b=\frac{\sum(X-\bar{X})(Y-\bar{Y})}{\sum(X-\bar{X})^{2}}=\frac{l_{X Y}}{l_{X X}}\)

三、直线回归中的统计推断

(一) 回归方程的假设检验

建立样本直线回归方程后，还需检验该直线回归关系是否确实存在，即样本回归系数b对应的总体回归系数是否有β ≠ 0。这一问题可用方差分析或与其等价的t检验来回答。

1. 方差分析

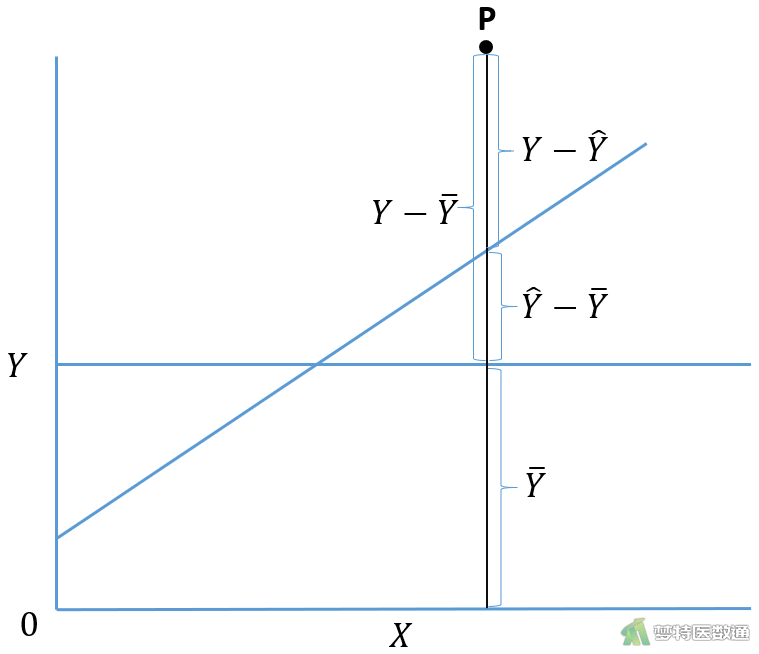
如图1所示，任一观察点P对应的纵坐标Y被回归直线\(\widehat{Y}\)和均数\(\overline{\mathrm{Y}}\)截成三段，即

\(\mathrm{Y}-\overline{\mathrm{Y}}=(\mathrm{Y}-\widehat{\mathrm{Y}})+(\widehat{\mathrm{Y}}-\overline{\mathrm{Y}})\)

将全部观察点都按上法处理，并将等式两端平方后再求和，则有：

\(\sum(\mathrm{Y}-\overline{\mathrm{Y}})^{2}=\sum(\mathrm{Y}-\widehat{\mathrm{Y}})^{2}+\sum(\widehat{\mathrm{Y}}-\overline{\mathrm{Y}})^{2}+2\sum(\mathrm{Y}-\widehat{\mathrm{Y}})(\widehat{\mathrm{Y}}-\overline{\mathrm{Y}})\)

由于\(\sum(\mathrm{Y}-\widehat{\mathrm{Y}})(\widehat{\mathrm{Y}}-\overline{\mathrm{Y}})\)展开后结果为0，则上式有：

\(\sum(\mathrm{Y}-\overline{\mathrm{Y}})^{2}=\sum(\mathrm{Y}-\widehat{\mathrm{Y}})^{2}+\sum(\widehat{\mathrm{Y}}-\overline{\mathrm{Y}})^{2}\)

用符号表示为：

\(\mathrm{SS}_{\text {总 }}=\mathrm{SS}_{\text{残 }}+\mathrm{SS}_{\text {回 }}\)

SS_总为Y的离均差平方和，表示未考虑Y与X的回归关系时Y的总变异。

SS_残为残差平方和。它反映了除X对Y影响之外的一切因素对Y的变异的作用，也就是在总平方和中无法用X解释的部分，表示考虑回归之后Y真正的随机误差。

SS_回为回归平方和，反应了在Y的总变异中可以用Y与X的直线关系解释的变异。

上述三个平方和，各有其相应的自由度v，并有如下的关系：

\(v_{\text {总 }}=v_{\text {残 }}+v_{\text {回 }},v_{\text {总 }}=\mathrm{n}-1,v_{\text{残}}=\mathrm{n}-2, v_{\text {回 }}=1\)

若两变量间总体回归关系确实存在，回归的贡献应大于随机误差，可计算如下F统计量：

\(F=\frac{\mathrm{SS}_{\text {回 }} / v_{\text{回 }}}{\mathrm{SS}_{\text {残 }} / v_{\text{残 }}}=\frac{\mathrm{MS}_{\text{回 }}}{\mathrm{MS}_{\text {残 }}}\)

式中MS_回、MS_残分别称为回归均方和残差均方。统计量F服从自由度为v_回v_残的F分布。查(F界值表)，得P值，按所取检验水准作出推断结论。

2. t检验

对β是否不为0这一假设，可以将b视为一个均数进行如下t检验

\(t=\frac{\mathrm{b}-0}{\mathrm{~S}_{\mathrm{b}}},v=\mathrm{n}-2\)

\(\mathrm{S}_{\mathrm{b}}=\frac{\mathrm{S}_{\mathrm{Y} \cdot \mathrm{X}}}{\sqrt{l_{\mathrm{XX}}}}\)

\(S_{\mathrm{Y} \cdot \mathrm{X}}=\sqrt{\frac{SS_{\text {残 }}}{n-2}}\)

式中S_YX为样本回归的剩余标准差(standard deviation of residuals)，即剩余均方开方。S_b为样本回归系数标准误。查(t界值表)，得P值，按所取检验水准作出推断结论。

(二) 总体回归系数β的置信区间

利用上述对回归系数的t检验，可以得到β的1-α置信区间为：

\(b \pm \mathrm{t}_{\alpha / 2, v} \cdot \mathrm{S}_{\mathrm{b}}\)

(三) 利用回归方程进行估计和预测

1. 总体均数\(\mu_{Y \mid X}\)的置信区间

给定X的数值X₀，由样本回归方程计算所得的\(\widehat{\mathrm{Y}}_{0}\)只是相应总体均数\(\mu_{Y \mid X}\)的一个点估计。反应其抽样误差大小的标准误公式为：

\(S_{\widehat{Y}_{0}}=S_{Y \cdot X}\sqrt{\frac{1}{n}+\frac{\left(X_{0}-\bar{X}\right)^{2}}{\sum(X-\bar{X})^{2}}}\)

给定X = X₀时，总体均数\(\mu_{Y \mid X}\)的1-α可信区间为：

\(\widehat{\mathrm{Y}}_{0} \pm \mathrm{t}_{\alpha/ 2, v} \cdot S_{\widehat{\mathrm{Y}}_{0}}\)

2. 个体Y值的预测区间

给定X的数值X₀，对应的个体Y值也存在一个波动范围。其标准差\(S_{Y_{0}}\)的计算公式为

\(S_{Y_{0}}=S_{\mathrm{Y} \cdot \mathrm{X}}\sqrt{1+\frac{1}{n}+\frac{\left(X_{0}-\bar{X}\right)^{2}}{\sum(X-\bar{X})^{2}}}\)

给定X = X₀时，个体Y值的1-α预测区间为

\(\widehat{\mathrm{Y}}_{0} \pm \mathrm{t}_{\alpha/ 2, v} \cdot S_{Y_{0}}\)

(四) 决定系数

决定系数(coefficient of determination)定义为回归平方和与总平方和之比，计算公式为：

\(\mathrm{R}^{2}=\frac{\mathrm{SS}_{\text{回 }}}{\mathrm{SS}_{\text {总 }}}\)

R²取值在0到1之间且无单位，其数值大小反映了回归贡献的相对程度，也就是在Y的总变异中回归关系所能解释的百分比。

四、案例数据

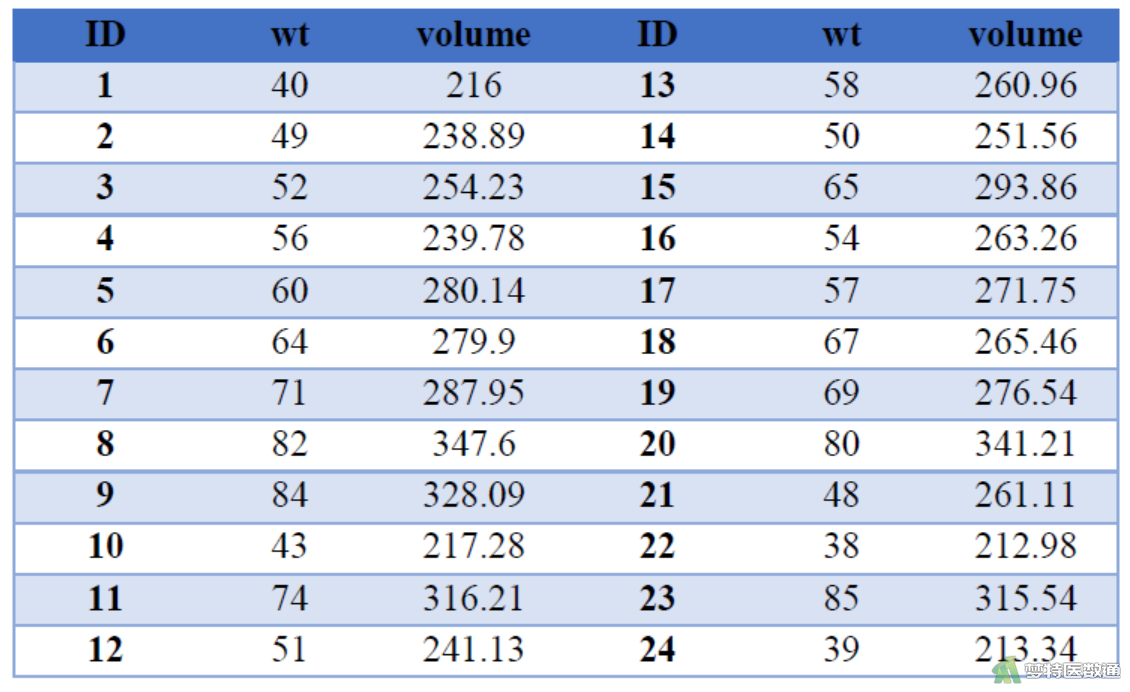
研究健康成年人的体重和双肾脏总体积(ml)的关系，测得24名健康成年人的体重wt (kg)与双肾脏总体积volume (ml)，拟探讨健康成年人的体重与双肾总体积是否有关，并希望通过健康成年人的体重预测双肾总体积。数据见图2。

五、案例分析

假设本案例满足简单线性回归分析的适用条件，下面构建其回归方程并进行建设检验。

(一) 建立直线回归方程

1. 计算X、Y的均数\(\overline{\boldsymbol{X}}\)、\(\overline{\boldsymbol{Y}}\)离均差平方和l_XX、l_YY与离均差积和l_XY

\(\bar{X}=\frac{\sum X}{n}=\frac{1436}{24}=59.83\)

\(\bar{Y}=\frac{\sum Y}{n}=\frac{6474.77}{24}=269.78\)

\(l_{X X}=\sum X^{2}-\frac{\left(\sum X\right)^{2}}{n}=90682-\frac{1436^{2}}{24}=4761.33\)

\(l_{Y Y}=\sum Y^{2}-\frac{\left(\sum Y\right)^{2}}{n}=178277.41-\frac{6474.77^{2}}{24}=35500.47\)

\(l_{X Y}=\sum X Y-\frac{\left(\sum X\right)\left(\sum Y\right)}{n}=399714.60-\frac{1436 * 6474.77}{24}=12307.53\)

2. 求回归系数b和截距a

\(b=\frac{l_{X Y}}{l_{XX}}=\frac{12307.53}{4761.33}=2.585\)

\(a=\bar{Y}-b \bar{X}=269.78-2.585 * 59.83=115.12\)

3. 列出直线回归方程

\(\widehat{\mathrm{Y}}=115.12+2.585 \mathrm{X}\)

(二) 回归方程的假设检验

1. 建立假设检验

H₀：β = 0，即健康成年人的体重和双肾脏总体积之间无直线关系；

H₁：β ≠ 0，即健康成年人的体重和双肾脏总体积之间存在直线关系。

α = 0.05

2. 方差分析

\(F=\frac{\mathrm{SS}_{\text {回 }} / v_{\text{回 }}}{\mathrm{SS}_{\text {残 }} / v_{\text{残 }}}=\frac{31813.621 / 1}{3686.844 /22}=189.837\)

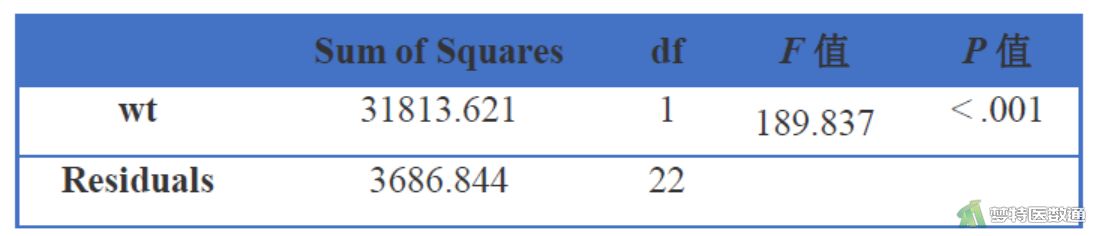
以v₁ = 1，v₂ = 22，查(F界值表)，得P< 0.001。按α= 0.05水准，拒绝H₀，接受H₁，可以认为健康成年人的体重和双肾脏总体积之间存在直线关系。

3. t检验

\(S_{\mathrm{Y} \cdot \mathrm{X}}=\sqrt{\frac{SS_{\text{残 }}}{n-2}}=\sqrt{\frac{3686.844}{22}}=12.945\)

\(S_{\mathrm{b}}=\frac{S_{\mathrm{Y} \cdot\mathrm{X}}}{\sqrt{l_{\mathrm{XX}}}}=\frac{12.945}{\sqrt{4761.33}}=0.188\)

\(t=\frac{\mathrm{b}-0}{\mathrm{~S}_{\mathrm{b}}}=\frac{2.585}{0.188}=13.75\)

以v = 22，查(t界值表)，得P < 0.001。按α = 0.05水准，拒绝H₀，接受H₁，可以认为健康成年人的体重和双肾脏总体积之间存在直线关系。

此处t²=13.75²= 189.1=F。

(三) 总体回归系数β的置信区间

β的95%置信区间为

\(\left(b-t_{\alpha / 2, v} \cdot\mathrm{S}_{\mathrm{b}}, b+t_{\alpha / 2, v} \cdot\mathrm{S}_{\mathrm{b}}\right)\)

\(=\left(2.585-t_{0.05 / 2,22} * 0.188,2.585+\mathrm{t}_{0.05 / 2,22} * 0.188\right)=(2.196,2.974)\)

(四) 决定系数

\(R^{2}=\frac{\mathrm{SS}_{\text{回 }}}{\mathrm{SS}_{\text{总 }}}=\frac{31813.621}{31813.621+3686.844}=0.896\)

综上，健康成年人的体重和双肾脏总体积之间存在直线关系，回归方程为volume = 115.119 + 2.585×wt，即体重每增加1kg，双肾脏总体积增加2.585ml；决定系数R²=0.896，表示此例中体重可解释双肾脏总体积变异性的89.6%。