Spearman相关性分析(Spearman Correlation Analysis)——R软件实现

关键词：R语言; R软件; 相关分析; Spearman相关分析; 连续变量相关分析; Spearman相关系数; 等级相关分析; 秩相关

一、案例介绍

某医师收集了224例肺癌患者的生存时间(Time)和患者自评的卡氏评分(pat.karno)。问患者自评的卡氏评分与其生存时间是否相关。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是检验患者自评的卡氏评分与其生存时间是否相关，即探究自评卡氏评分与生存时间的相关性，两个变量均为定量变量，可以采用Pearson相关性分析或Spearman相关性分析。若使用Spearman相关性分析需要满足两个条件：

条件1：两个定量变量中至少有一个为非正态分布或总体分布未知或为等级资料。

条件2：两变量之间为单调关系。

三、软件操作及结果解读

(一) 导入数据

mydata <- read.csv("Spearman相关性分析.csv")  #导入CSV数据
View(mydata)  #查看数据

在数据栏目中可以查看全部数据情况，数据集中共有2个变量和224个观察对象，2个变量分别代表生存时间(Time)和卡氏评分(pat.karno)。

如果数据集较大也可使用如下命令查看数据框结构：

str(mydata) #查看数据框结构

(二) 适用条件判断

1. 条件1判断(正态性检验)

(1) 软件操作

## 绘制Q-Q图 ##

par(mfrow = c(1, 2))  #绘制一行2个图片
qqnorm(mydata$Time, ylab="day", main="Time")  #绘制Time的qq图
qqline(mydata$Time)  #增加趋势线
qqnorm(mydata$pat.karno, ylab="score", main="pat.karno")  #绘制pat.karno的qq图
qqline(mydata$pat.karno)  #增加趋势线

## 正态性检验 ##

shapiro.test(mydata$Time) #检验Time的正态性
shapiro.test(mydata$pat.karno) #检验pat.karno的正态性

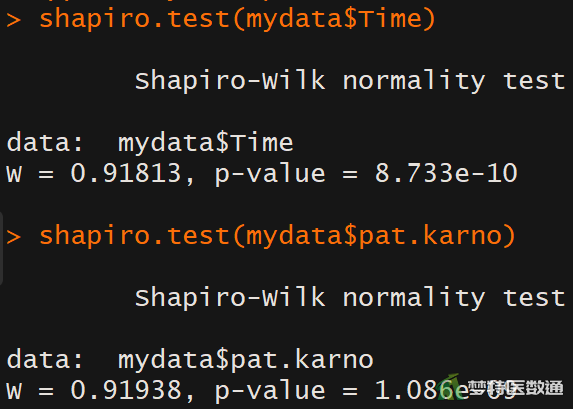
(2) 结果解读

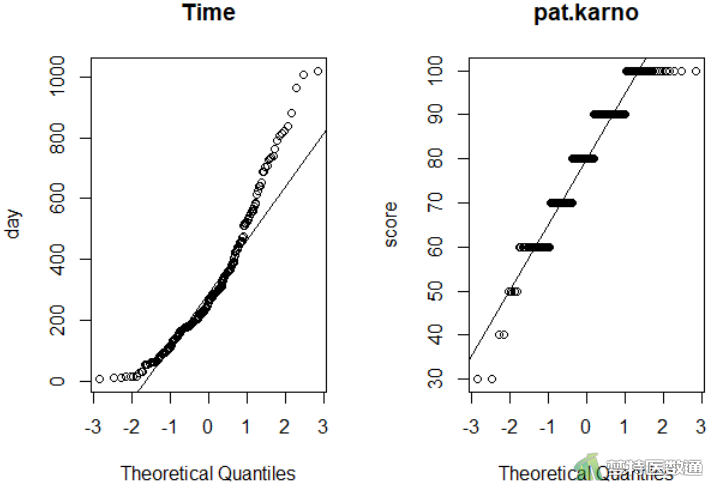
图3和图4给出了正态分布的图示和假设检验结果。图3的Q-Q图上两个变量的散点偏离对角线分布的较多，提示两个变量不服从正态分布；图4的正态性检验结果两个变量的正态性检验的P值均<0.001，也提示不满足正态性要求。综上，数据不服从正态分布。

2. 条件2判断(单调性判断)

(1) 软件操作

## 单调性判断 ##

library(ggplot2)
ggplot(data=mydata,aes(x=pat.karno,y=Time))+
  geom_point()+stat_smooth(method="lm",se=TRUE) #散点图+拟合线

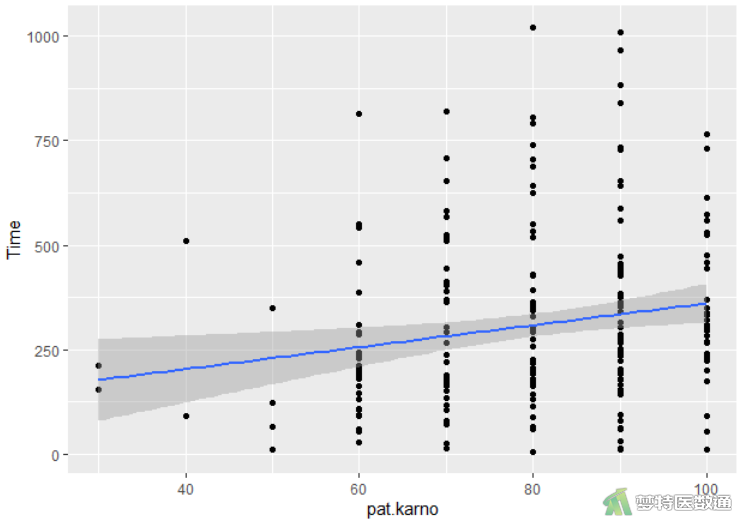
(2) 结果解读

由图5中“pat.karno”与“Time”的散点分布及拟合线可知，两变量整体呈现单调性分布，表明数据满足条件2。

 (三) 统计描述及推断

1. 软件操作

## 相关性分析 ##

cor.test(mydata$pat.karno,mydata$Time,alternative = "two.side",method = "spearman",conf.level = 0.95)

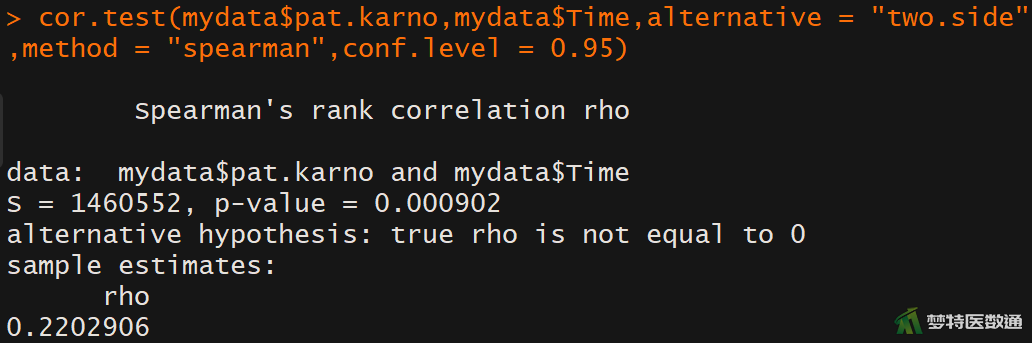
2. 结果解读

图6的“cor.test (相关性分析)”分析结果给出了患者自评卡氏评分(pat.karno)与生存时间(Time)的Spearman相关系数和假设检验的P值。可知，患者的自评卡氏评分与生存时间有相关性，Spearman相关系数r_s=0.220，P<0.001，两变量间呈弱相关。

四、结论

本研究采用Spearman相关性分析对患者自评卡氏评分(pat.karno)与生存时间(Time)的相关性进行了检验。通过Q-Q图和Shapiro-Wilk检验，提示数据为偏态分布，通过绘制散点图显示两变量之间呈单调关系。

Spearman相关性分析结果显示，患者的自评卡氏评分与生存时间之间为正相关(r_s=0.220，P<0.001)，卡氏评分越高，患者的生存时间越长，但相关性程度较弱。

五、分析小技巧

• Spearman相关，又称秩相关、等级相关，是对两变量的秩次大小作线性相关分析，对原始变量的分布不作要求，属于非参数统计方法，适用范围较广。对于服从Pearson相关的数据亦可计算Spearman相关系数，但统计效能更低。
• Spearman相关系数(r_s)介于-1与1之间，r_s >0为正相关，r_s <0为负相关。r_s的绝对值(|r_s|)越大，变量间的相关性越强。
• 参考Pearson相关系数对r_s进行等级划分：当0.9</r/<1，为高度相关；当0.7</r/<0.9，为强相关；0.4</r/<0.7，为中度相关；0.2</r/<0.4，为弱相关性；0</r/<0.2，为极弱相关或无相关性