Pearson相关性分析主要用于分析满足正态分布的两定量变量之间的关系,若两变量中包含等级变量,或变量不符合正态分布,或变量分布类型未知时,可以采用另一种相关性分析方法——Spearman等级相关性分析。
Spearman相关性分析的基本思想是:分别对两个变量X、Y做秩变换(rank transformation),用秩次RX和RY表示;然后按Pearson相关性分析的方法计算RX和RY的相关性。对于满足Pearson相关性分析的数据,亦可以使用Spearman相关性分析,但统计效能要低。本篇文章将介绍Spearman相关性分析的适用条件及假设检验。
关键词:相关分析; Spearman相关分析; 连续变量相关分析; Spearman相关系数; 等级相关分析; 秩相关
一、适用条件
Spearman相关性分析,需要满足2个条件:
条件1:变量包含等级变量、或变量不服从正态分布或分布类型未知。
条件2:两变量之间存在单调关系。
二、统计量计算
(一) Spearman相关系数
计算Spearman相关系数rs的过程为:
先将变量X、Y分别从小到大排序编秩,用秩次RX和RY表示。排序时,出现数据相等从而造成秩次相同的现象称为相持(tie),此时,取其平均秩次为每个数据的秩次。Spearman相关系数rs的计算公式为:
\(r_{s}=\frac{\sum\left(R_{X}-\overline{R_{X}}\right)\left(R_{Y}-R_{Y}\right)}{\sqrt{\sum\left(R_{X}-\overline{R_{X}}\right)^{2} \sum\left(R_{Y}-\overline{R_{Y}}\right)^{2}}}=\frac{\sum R_{X} R_{Y}-\frac{\left(\sum R_{X}\right)\left(\sum R_{Y}\right)}{n}}{\sqrt{\left(\sum R_{X}^{2}-\frac{\left(\sum R_{X}\right)^{2}}{n}\right)\left(\sum R_{Y}^{2}-\frac{\left(\sum R_{Y}\right)^{2}}{n}\right)}}\)与Pearson相关系数的计算公式对比, Spearman相关系数的计算公式只是将Pearson相关系数公式中的X、Y替换为了RX、RY。
(二) 假设检验
对总体相关系数ρs是否为0做零假设检验,根据样本含量n的大小有两种方法:
1. 查表法
当样本含量n≤50时,根据样本含量n查(rs界值表)。若|rs|≥rs(a,n),则P≤α,即两变量相关;若|rs|<rs(a,n),则P>α,两变量不存在相关关系。
2. t检验
当n>50时,根据下式计算统计量t值:
\(t=\frac{\left|r_{s}\right|}{\sqrt{\frac{1-r_{s}^{2}}{n-2}}}, v=n-2\)计算得到t值后,结合自由度υ,查(t界值表),获得P值。
三、案例数据
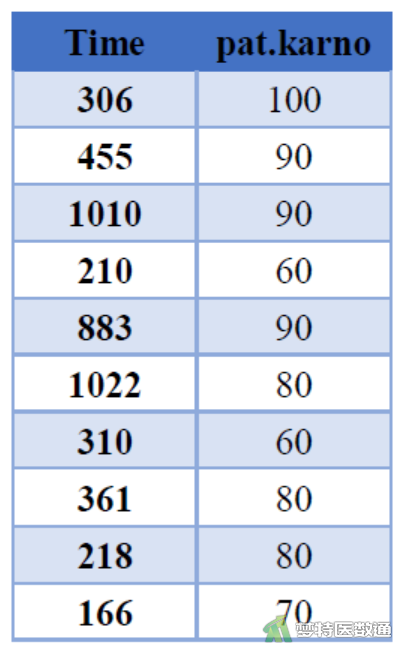
某医师收集了224例肺癌患者的生存时间(Time)和患者自评的卡氏评分(pat.karno)。问患者自评的卡氏评分与其生存时间是否相关?部分数据如图1所示。
四、案例分析过程
(一) 适用条件判定
1. 正态性检验
对生存时间(Time)和患者自评的卡氏评分(pat.karno)分别绘制Q-Q图,如图2-1和图2-2所示。
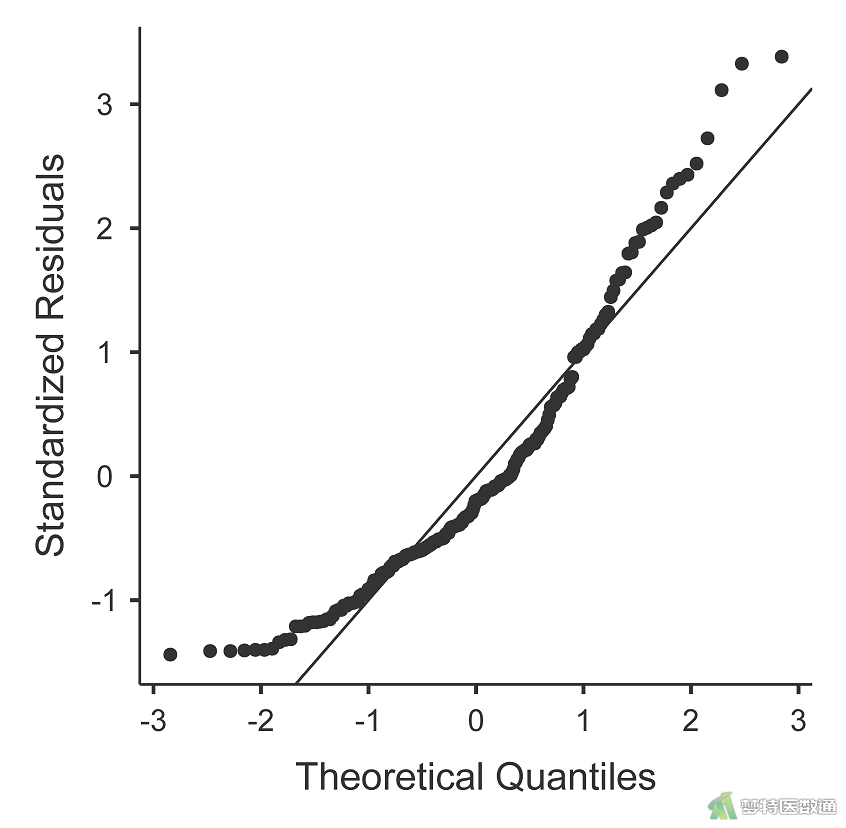
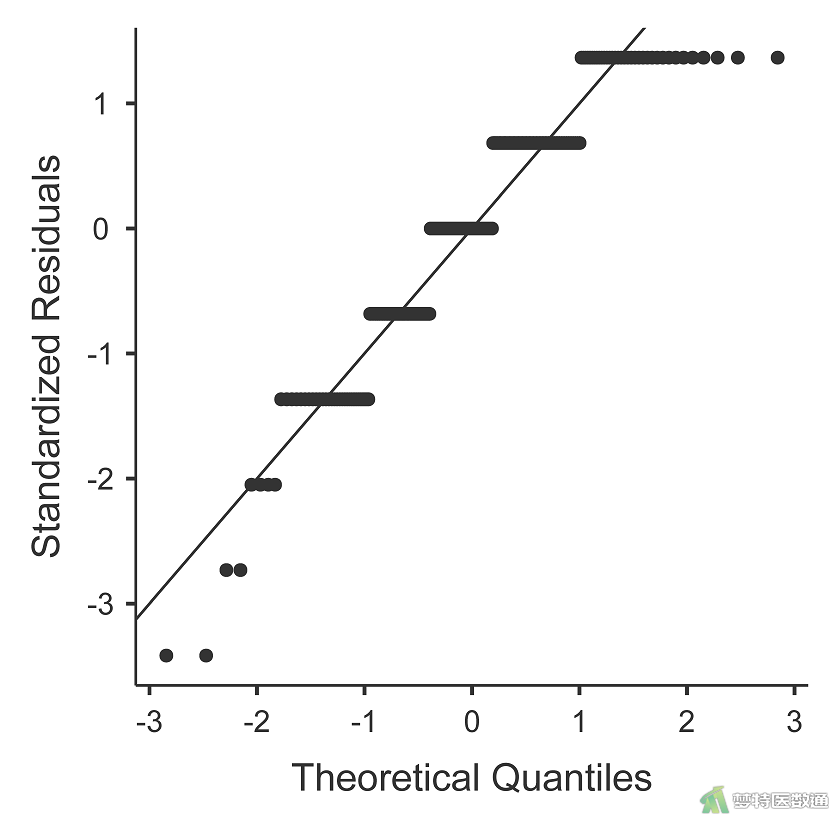
两个变量的散点偏离对角线分布的较多,提示两个变量不服从正态分布;此外,也可对两变量进行Shapiro-Wilk正态性检验,P值均<0.001,也提示两变量不满足正态性要求(读者可自行操作)。
2. 单调性判断
对生存时间(Time)和患者自评的卡氏评分(pat.karno)绘制散点图,如图3所示。
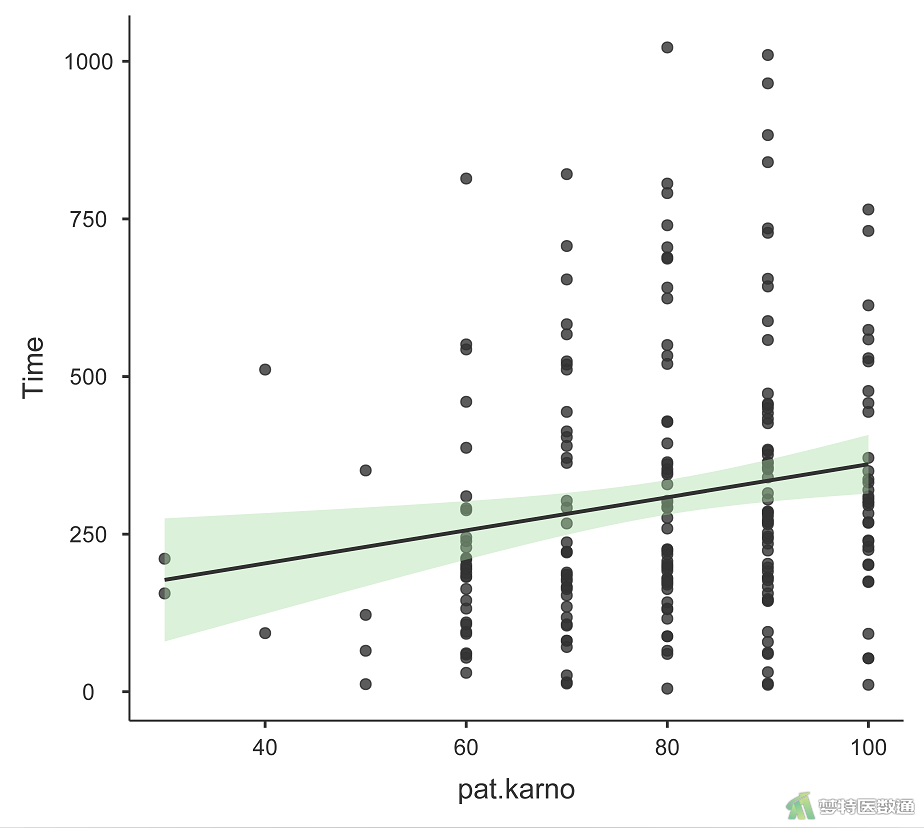
如图所示,生存时间(Time)随卡氏评分(pat.karno)的增加而增加,两变量呈单调关系。
综上,本案例数据可使用Spearman等级相关进行分析。
(二) 计算样本相关系数
首先,将生存时间(Time)和患者自评的卡氏评分(pat.karno)分别从小到大排序编秩,用秩次RX和RY表示,部分数据结果如图4所示。
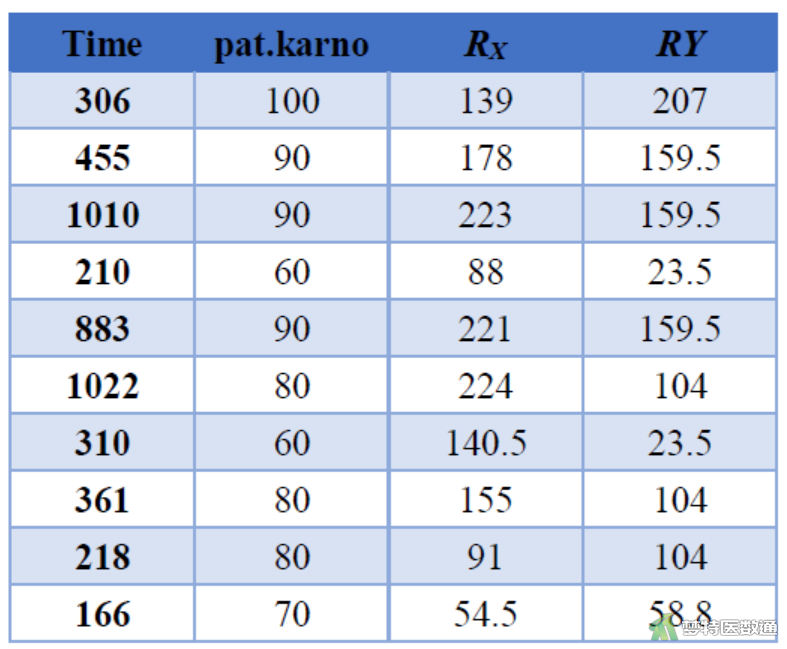
然后,根据rs计算公式可求得
\(r_{s}=\frac{\sum R_{X} R_{Y}-\frac{\left(\sum R_{X}\right)\left(\sum R_{Y}\right)}{n}}{\sqrt{\left(\sum R_{X}^{2}-\frac{\left(\sum R_{X}\right)^{2}}{n}\right)\left(\sum R_{Y}^{2}-\frac{\left(\sum R_{Y}\right)^{2}}{n}\right)}}=0.220\)(三) 假设检验
接下来,进一步检验rs是否来自ρs=0的总体,检验步骤如下:
1. 建立检验假设,确定检验水准
H0:ρs=0,肺癌患者的生存时间与患者自评的卡氏评分无相关关系
H1:ρs≠0,肺癌患者的生存时间与患者自评的卡氏评分有相关关系
α = 0.05
2. 计算检验统计量
本案例数据量n=224,使用t检验法,根据t值计算公式可计算统计量:
\(t=\frac{\left|r_{s}\right|}{\sqrt{\frac{1-r_{s}^{2}}{n-2}}}=3.365, \quad v=n-2=224-2=222\)3. 确定P值,作出推断结论
按自由度222查(t界值表),得P<0.001。按α = 0.05水准,拒绝H0,接受H1,生存时间与患者自评的卡氏评分有相关关系。
(四) 结论
肺癌患者的生存时间与患者自评的卡氏评分呈正相关,相关系数r为0.220 (t=3.365,P<0.001)。
五、知识小贴士
- Spearman相关,又称秩相关、等级相关,是对两变量的秩次大小作线性相关分析,对原始变量的分布不作要求,属于非参数统计方法,适用范围较广。对于服从Pearson相关的数据亦可计算Spearman相关系数,但统计效能更低。
- Spearman相关系数(rs)介于-1与1之间,rs >0为正相关,rs <0为负相关。rs的绝对值(|rs|)越大,变量间的相关性越强。
- 参考Pearson相关系数对rs进行等级划分:当0.9</r/<1,为高度相关;当0.7</r/<0.9,为强相关;0.4</r/<0.7,为中度相关;0.2</r/<0.4,为弱相关性;0</r/<0.2,为极弱相关或无相关性。