两因素重复测量方差分析(Two-way Repeated-Measures ANOVA)一(无交互作用)——SAS软件实现

关键词：SAS; 重复测量; 重复测量资料; 重复测量方差分析; 两因素重复测量方差分析; 球形检验; 交互作用; 主效应; 单独效应

一、案例介绍

研究A、B两种饲料对家兔的增重效果，选择20只家兔，随机分成两组，第一组用饲料A饲养，第二组用饲料B饲养，并于试验开始后第一个月(time1)、第二个月(time2)、第三个月(time3)分别测量2组家兔体重，试比较A、B两种饲料对家兔的增重效果有无差别？数据见图1。本文案例可从“附件下载”处下载。

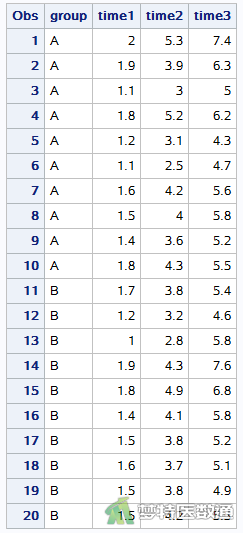
二、问题分析

本案例的分析目的是比较A、B两种饲料对家兔的增重效果有无差别。由于3个时间点的数据属于重复测量数据，且有两个组别，可以使用两因素(时间因素time和分组因素group)重复测量方差分析。但需要满足以下6个条件：

条件1：观察变量唯一，且为连续变量。本研究中观察变量只有体重，且为连续变量，该条件满足。

条件2：有两个分析因素。本研究有时间因素time和分组因素group两个因素，该条件满足。

条件3：观察变量为重复测量数据，即不满足独立性。本研究中两个组别在3个时间点时测量的体重均是针对同一批样本，因此不满足独立性，该条件满足。

条件4：观察变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件5：各组、各水平(时间点)观察变量为正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件6：相互比较的各处理水平(组别)的总体方差齐，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

①利用LIBNAME语句建立SAS逻辑库关联，注意逻辑库名称要求，即最大长度8字符，必须以字母或下划线“_”开始，可以是字母、数字和下划线的任意组合。具体代码如下：

libname mydata ‘D:\mydata’;

通过这一步骤，SAS能够识别引号中的物理位置，将逻辑库建立在该目录下，同时在以下过程中新建的SAS表格便可以永久储存在该位置，便于反复读取和使用。先运行该代码使其生效。

②利用PROC IMPORT语句导入文件，代码如下：

proc import out= mydata.example
    datafile=" D:\mydata\两因素重复测量方差分析一.csv"
	  dbms=csv replace;
	  getnames=yes;
run;

该过程在mydata逻辑库中生成example数据集，数据文件由DATAFILE=选项指定，DBMS=选项指定其数据库类型。该案例中初始数据集为csv文件，故而使用“dbms=csv”指定。如果已经存在相同名称的SAS数据集，即可使用REPLACE选项进行覆盖。GERNAMES=YES选项指定从第2行开始读取数据，将数据集的首行变量名作为SAS数据集的变量名。

(二) 适用条件判断

1. 条件4判断(异常值判断)

(1) 软件操作

运用UNIVARIATE过程进行检验：

proc univariate data= mydata.example plot;
var time1 time2 time3;
by group;
run;

其中“mydata.example”为上一步中导入的数据集名称，“time1”、“time2”、“time3”为分析变量名，即分别为3个时间点检测的家兔体重。“by group”表示分A、B两组分别对三个时间点的家兔体重进行异常值判断。因此将会出现6个检验结果，总结如图2：

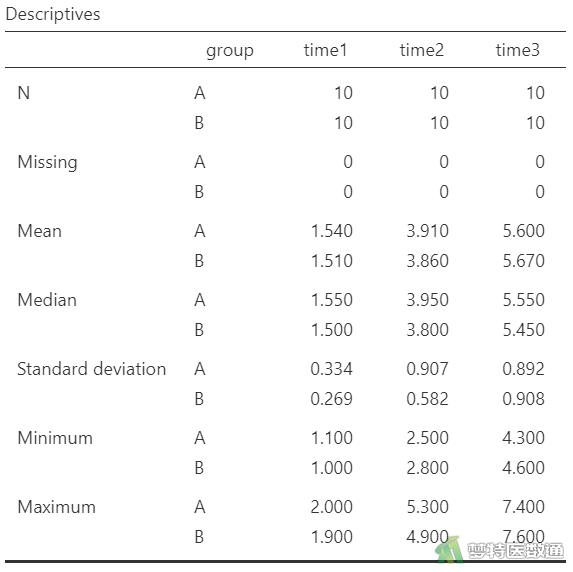
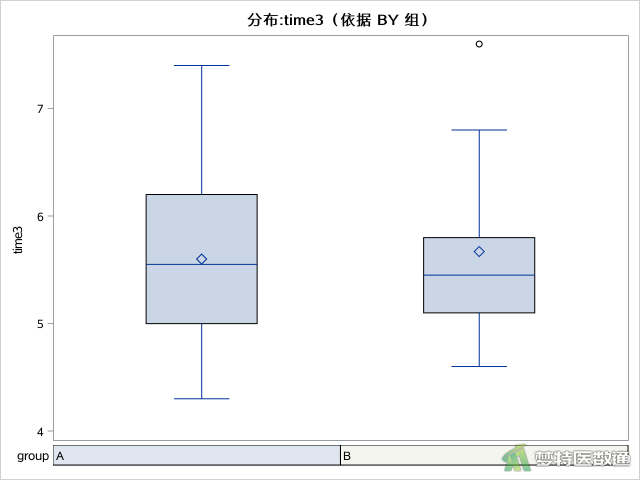
描述数据分布情况的箱线图，见图3-1—图3-3所示。

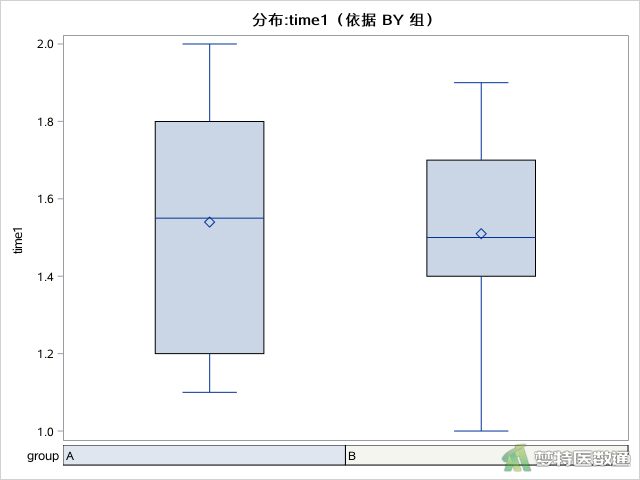
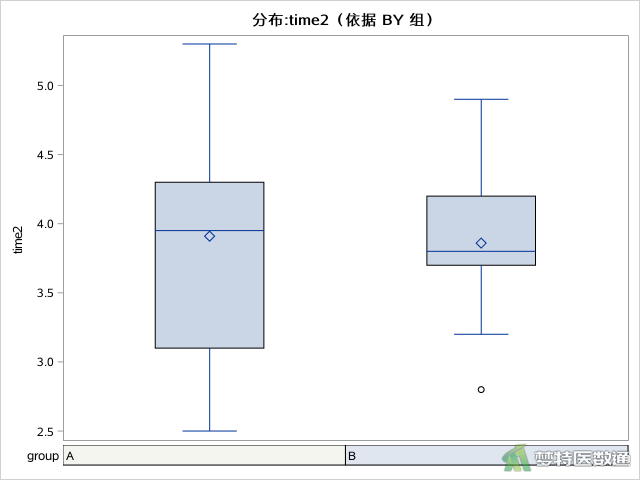
(2) 结果解读

图2“Descriptives (描述性分析)”表格中，总结出了各组观察变量的最小值和最大值，依据专业尚不能认为存在异常值；此外，图3-1—图3-3中的箱线图也未提示任何异常值。综上，本案例未发现需要删除的异常值，满足条件4。

2. 条件5判断(正态性检验)

(1) 软件操作

运用UNIVARIATE 过程对两组各时间点的家兔体重进行正态性检验，示例代码如下： 

proc univariate data= mydata.example normal;
var time1 time2 time3;
by group;
run;

两因素重复测量方差分析时，需要分别考察每一组的正态性情况，因此将会出现6种检验结果，总结如图4：

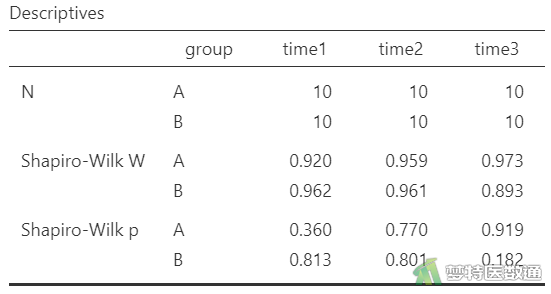
(2) 结果解读

图4的正态性检验结果显示A组3个时间点P=0.360、0.770、0.919，B组三个时间点P=0.813、0.801、0.182，均>0.1，提示各组数据均服从正态分布。此外，本案例也可以绘制Q-Q图，结果也提示各组数据均服从正态分布(请读者自行操作)。综上，本案例满足条件5。关于正态性检验的注意事项详见文章(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。

3. 条件6判断(方差齐性检验)

(1) 软件操作

proc anova data=mydata.example;
	class group;
  	model time1 time2 time3=group;
	means group / hovtest=levene(type=abs);
run;

(2) 结果解读

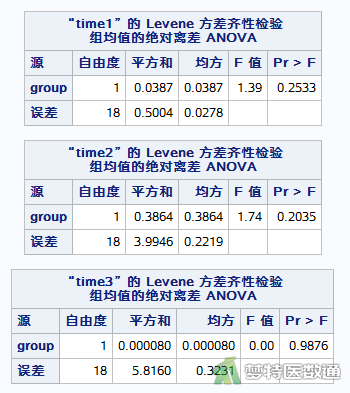
图5 “Homogeneity of Variances Test (Levene’s) (Levene’s方差齐性检验)”表格显示，time1、time2、time3时，两组之间的方差齐性检验结果分别为F=1.39、P=0.2533，F=1.74、P=0.2035，F=0.00、P=0.9876；提示每个时间点的两组之间都满足方差齐性。本案例满足条件6。关于方差齐性检验的更多内容请阅读(医学统计学核心概念及重要假设检验的软件实现(4/4)——方差齐性检验及SPSS实现)。

(三) 球形假设检验

1. 软件操作

proc glm data=mydata.example;
	class group;
  	model time1 time2 time3=group;
    repeated time 3/printe;
run;

通过printe进行球形检验，结果如图6中“正交成分”所示。

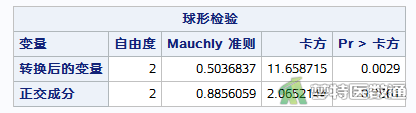
2. 结果解读

由图6的球形检验结果可知，W=0.886，P=0.3561，表示满足球形假设。因此本案例可以直接采用非校正方法分析的结果。

(四) 统计描述

1. 软件操作

proc glm data=mydata.example;
  class group;
  model time1 time2 time3 = group;
  repeated time 3 ;
  lsmeans group/out=means;
run;

proc sort data=means;by group _name_;
proc print;run;

proc glm data=mydata.example;
	class group;
	model time1-time3 = group;
	output out=out lclm=time1-time3 uclm=time1-time3;
run;

proc print data=out;run;
data out;
	set out;
    length time_1 $25 time_2 $25 time_3 $25;
	time_1=compress(put(time12,6.3)) || '-' || compress(put(time13,6.3));
	time_2=compress(put(time22,6.3)) || '-' || compress(put(time23,6.3));
	time_3=compress(put(time32,6.3)) || '-' || compress(put(time33,6.3));
proc print;run;

proc transpose data=out out=out1(drop=ci2-ci10) prefix=CI;
	var time_1-time_3;     
	by group; 
proc print;run;

proc sort data=out1;
by group _name_;
proc print;run;

data a;
merge out1 means;
CI=CI1;
label group='分组' _NAME_='时间点' CI='置信区间' LSMEAN='均值' STDERR='标准误'; 
drop CI1;
proc print label;run;

proc transpose data=out out=out2(keep = group _NAME_ _LABEL_ CI1) prefix=CI;
	var time12 time22 time32;     
	by group; 
proc print;run;
proc transpose data=out out=out3(keep = group _NAME_ _LABEL_ CI2) prefix=CI;
	var time13 time23 time33 ;     
	by group; 
proc print;run;

data combine(rename=(LSMEAN=MEAN));
merge out2 out3 means;
drop _NAME_;
proc print;run;

proc sgplot data=combine;
 scatter x=_label_ y=mean/ yerrorupper=CI2 yerrorlower=CI1 group=group groupdisplay=cluster clusterwidth=0.2;
 series x=_label_ y=mean/group=group groupdisplay=cluster clusterwidth=0.2;
run;

2. 结果解读

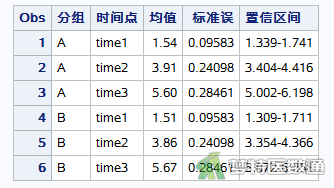
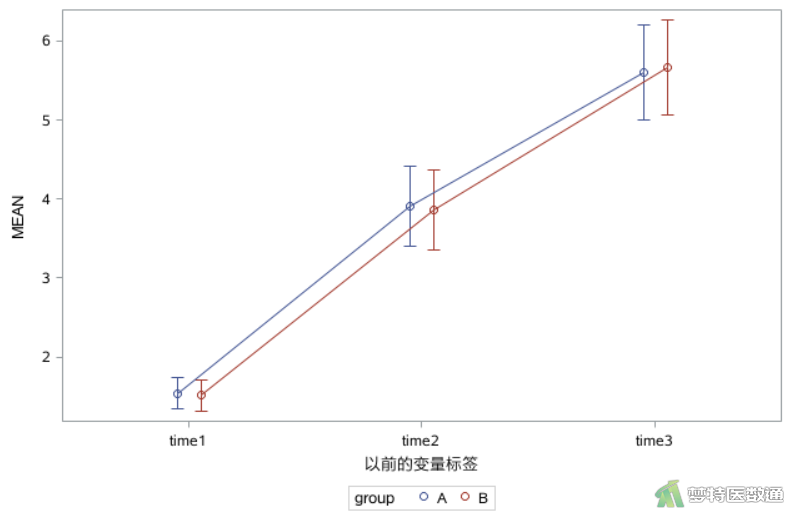
为了结果解释方便，首先在图7中总结了A、B两组在3个时间点的均值和标准差及其95%置信区间，图8则直观展示了两组的变化趋势。图7列出了A、B两组time1、time2、time3时间点的均值分别为1.54、3.91、5.60 kg和1.51、3.86、5.67 kg。图8绘制了两组三个时间点体重的变化情况，可见两组的体重均有增加，并且增加的幅度基本保持一致。

(五) 交互作用判断

由于本案例有两个因素(一个为时间因素time，另一个为分组因素group)，因此需要首先判断两个因素之间是否存在交互作用。如果交互作用有统计学意义，则需要分析单独效应。

1. 软件操作

proc glm data=mydata.example;
	class group;
  	model time1 time2 time3=group/nouni;
    repeated time 3(0 1 2) contrast(1)/printe summary;
run;

2. 结果解读

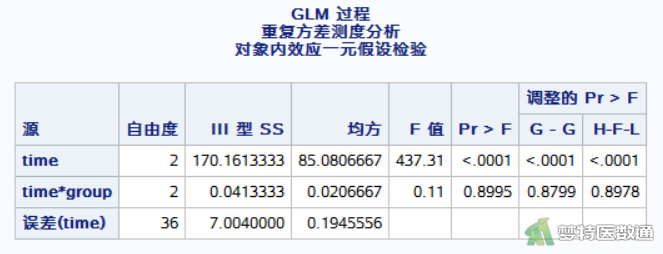
图9显示，time与group之间的交互作用结果为F_time*group=0.11，P=0.8995，提示time与group之间的交互作用无统计学意义。因此，本案例可直接以主效应分析结果进行判断，如果交互作用有统计学意义，则需要分析单独效应。

(六) 时间效应分析

以“Within Subjects Effects (主体内对比效应)”中time的检验结果可知，F_time=437.308，P<0.001(图9)，认为体重变化具有时间变化趋势。

(七) 组间效应分析

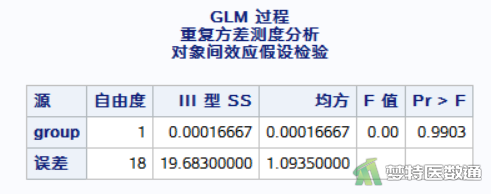
以图10中group的检验结果可知，F_group<0.001，P=0.9903，表示两种饲料对家兔的增重效果差异无统计学意义。

(八) 事后检验(两两比较)

上面分析得出了“体重变化具有时间趋势”的结论，即不同时间点体重差异有统计学意义，但具体是哪些时间点之间存在差异尚不清楚，因此需要进行事后检验，开展两两比较。

1. 软件操作

proc glm data=mydata.example;
	class group;
  	model time1 time2 time3=group/nouni;
    repeated time 3(0 1 2) contrast(1)/printe summary;
run;

程序中repeated time 3(0 1 2) contrast(1)/printe summary;可展示以time1为参照的两两比较结果，通过修改contrast(1)中的数字，可以改变参照组，进而得到不同时间点之间的两两比较结果，见图11-图12。

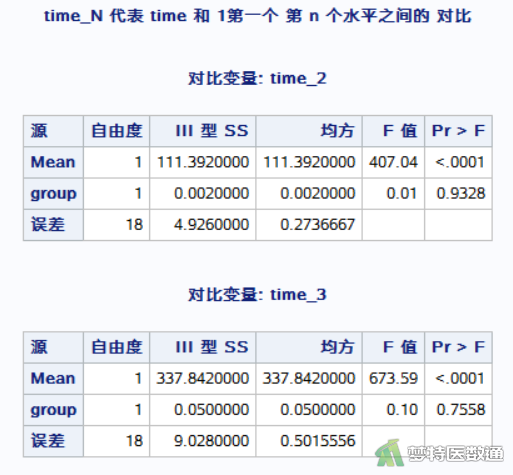
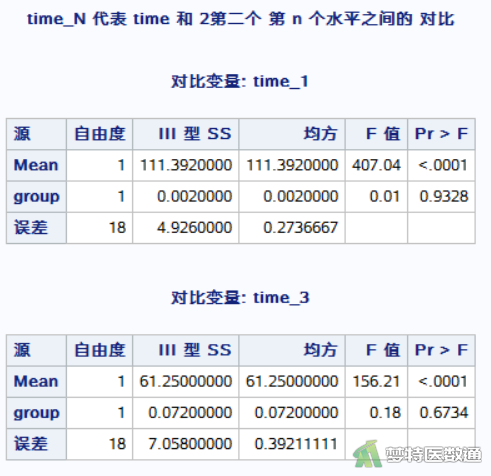
2. 结果解读

图11和图12提供了各时间点两两比较的 “df (自由度)”、“F (统计量F值)”、“P (未校正P值)”。可知，差异均有统计学意义(P<0.001)。

四、结论

本研究采用两因素重复测量方差分析比较A、B两种饲料对家兔的增重效果有无差别。通过专业知识判断，数据不存在异常值；通过Shapiro-Wilk检验，提示各组数据服从正态分布；通过Levene’s检验，提示每个时间点的两组之间都满足方差齐性；球形度检验提示，满足球形假设(W=0.886，P=0.3561)；组别与time无交互作用(F_time*group=0.11，P=0.8995)，故进行主效应分析。

A、B两组在试验开始后第1个月、第2个月和第3个月时的体重分别为1.540±0.334、3.910±0.907、5.600±0.892 kg和1.510±0.269、3.860±0.582、5.670±0.908 kg。两因素重复测量方差分析结果显示，在试验开始后第一个月、第二个月和第三个月时2组家兔的体重均呈上升趋势(F_time=437.31，P<0.001)，但两种饲料对家兔的增重效果差异无统计学意义(F_group=0.00，P=0.9903)。进一步采用“Bonferroni”校正法进行两两比较可知，随着时间的延长，试验开始后第第2个月和第3个月与第1个月试验开始时相比，体重增加均有统计学意义(P<0.001)。综上，两种饲料对家兔的增重效果无差异。