主成分评价(Principal Components Evaluation)——SPSS软件实现

关键词：SPSS; 主成分分析; 主成分评价; PCA; 降维; 多元统计分析

一、案例介绍

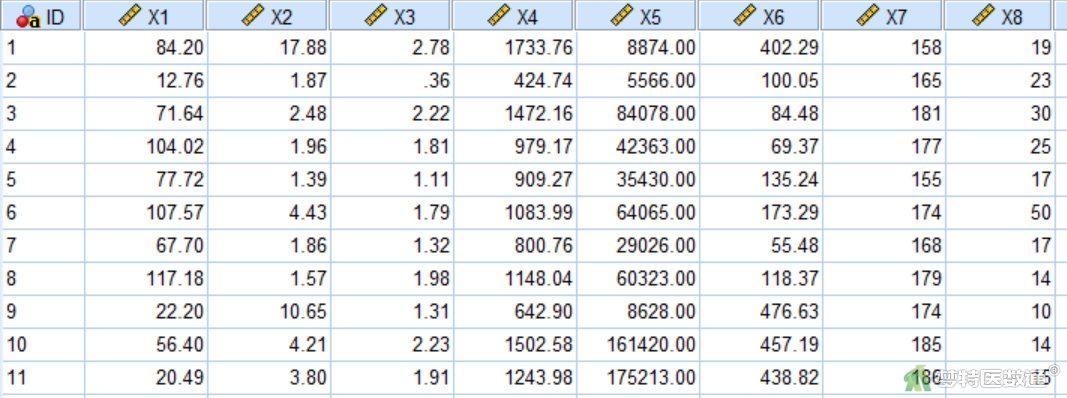
以主成分分析(Principal Components Analysis)——SPSS软件实现案例为例。某研究获得某省份30个景区旅游竞争力评价指标，具体如下：年旅游人数(万人)、年景区住宿人数(万人)、人均住宿天数(天)、国内游客平均消费(元)、国际游客平均消费(元)、景区设施投资(万元)、景区工作人员数(人)、景区导游数(人)。对景区旅游竞争力进行综合评价。

定义变量，将年旅游人数(万人)、年景区住宿人数(万人)、人均住宿天数(天)、国内游客平均消费(元)、国际游客平均消费(元)、景区设施投资(万元)、景区工作人员数(人)、景区导游数(人)，分别定义为X1，X2，X3，X4，X5，X6，X7，X8。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

在主成分分析(Principal Components Analysis)——SPSS软件实现一文中通过主成分分析提取出了三个主成分。本文继续利用该文的分析结果，对景区旅游竞争力进行综合评价。

三、计算综合排名指数

提取出的主成分可从不同方面反应旅游竞争力，但单独使用某一个主成分很难全面地做出综合评价，此时可考虑计算综合排名指数(Comprehensive ranking index)进行排名。综合排名指数为各主成分以各自的方差贡献率比例(特征值比例)为权重计算的得分之和，其计算公式如下：\(C=\frac{\lambda_{1}}{\lambda_{1}+\lambda_{2}+\lambda_{3}} \times F 1+\frac{\lambda_{2}}{\lambda_{1}+\lambda_{2}+\lambda_{3}} \times F 2+\frac{\lambda_{3}}{\lambda_{1}+\lambda_{2}+\lambda_{3}} \times F 3\)

其中λ_i代表第i个主成分因子的特征值，F_i代表主成分。

此处根据主成分计算的方法不同，分别介绍2种综合排名指数计算方法。

(一) 方法一

用因子载荷除以各根号下的特征值，得到主成分系数，然后用主成分系数乘以标准化后的自变量，得到主成分。该种计算方法是主成分分析(Principal Components Analysis)——SPSS软件实现一文所介绍方法，此处直接使用该文中计算好的结果。

综合排名指数计算过程如下：

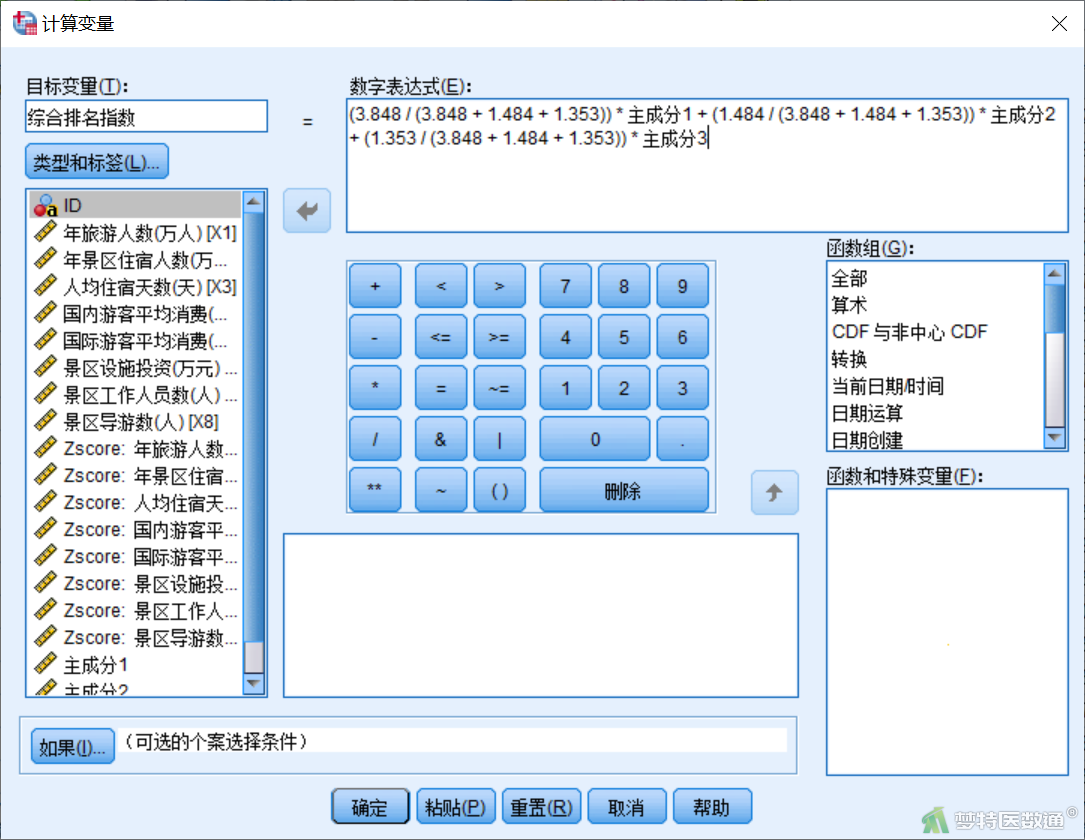
选择“转换”—“计算变量”，目标变量中输入“综合排名指数”，数字表达式中输入“(3.848 / (3.848 + 1.484 + 1.353)) * 主成分1 + (1.484 / (3.848 + 1.484 + 1.353)) * 主成分2 + (1.353 / (3.848 + 1.484 + 1.353)) * 主成分3”(图2)，即可生成各景区的综合排名指数。

然后对综合排名指数按照降序排列(图3)。

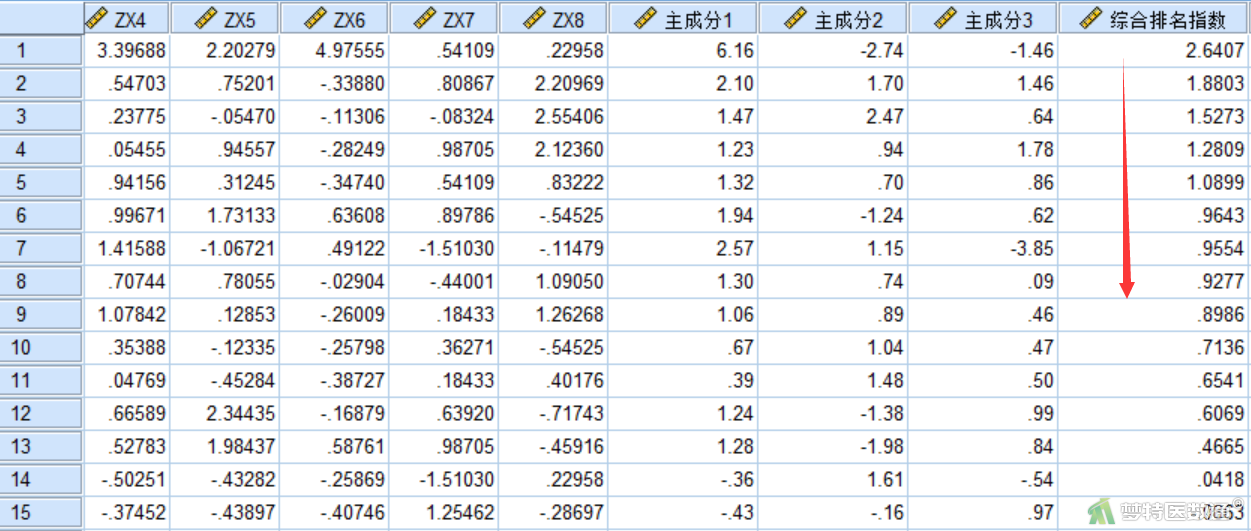
图4为排名结果，可以发现前5位景区排名分别为19、16、6、18、3。

(二) 方法二

除了上述方法一计算主成分以外，还可以利用未旋转因子分析的得分系数成乘以根号下特征值计算主成分，操作如下：

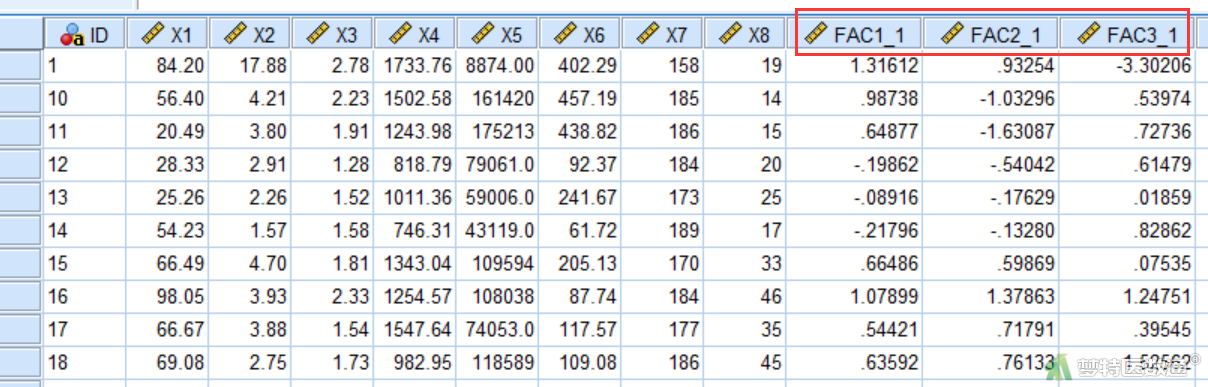
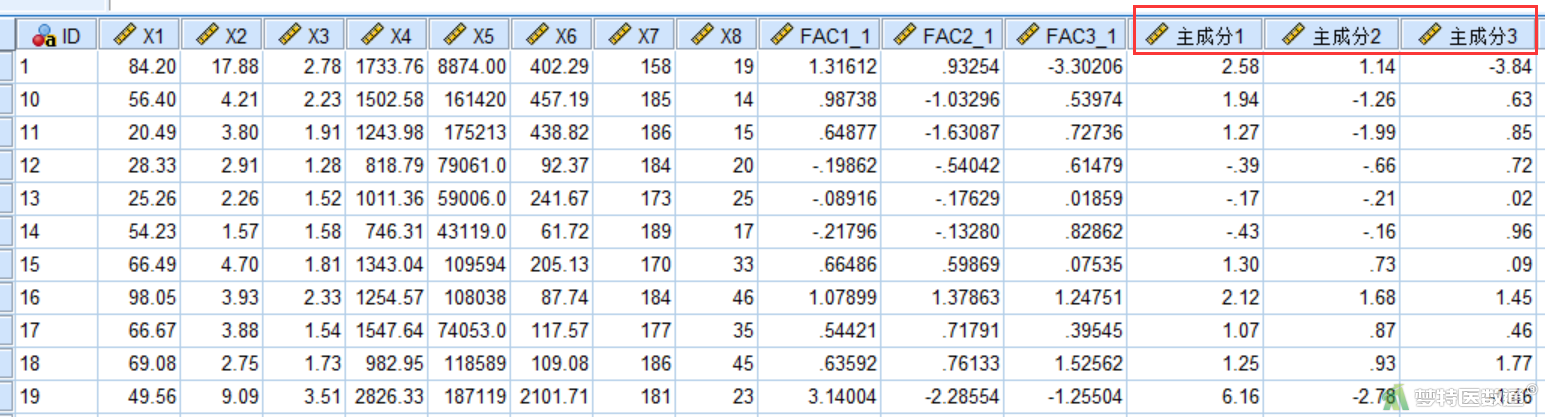
在主成分分析过程中，点击“得分”选项，勾选“保存为变量”，“方法”选择“回归”(图5)。即可在页面视图生成三个主成分的得分系数，见图6。

按照图7所示计算主成分1，依次可计算主成分2和主成分3，结果如图8所示。可见和方法一计算的结果基本一致。

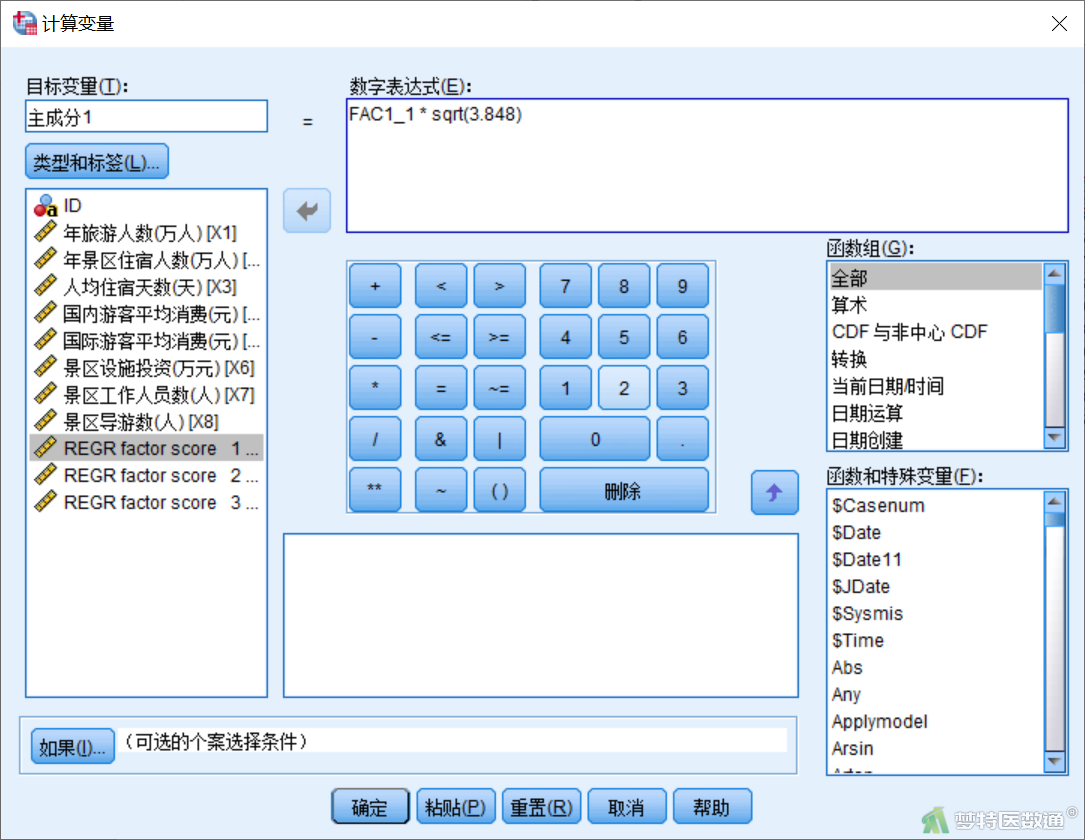
然后按照方法一过程计算综合排名指数，并进行排名。

四、百分制转换

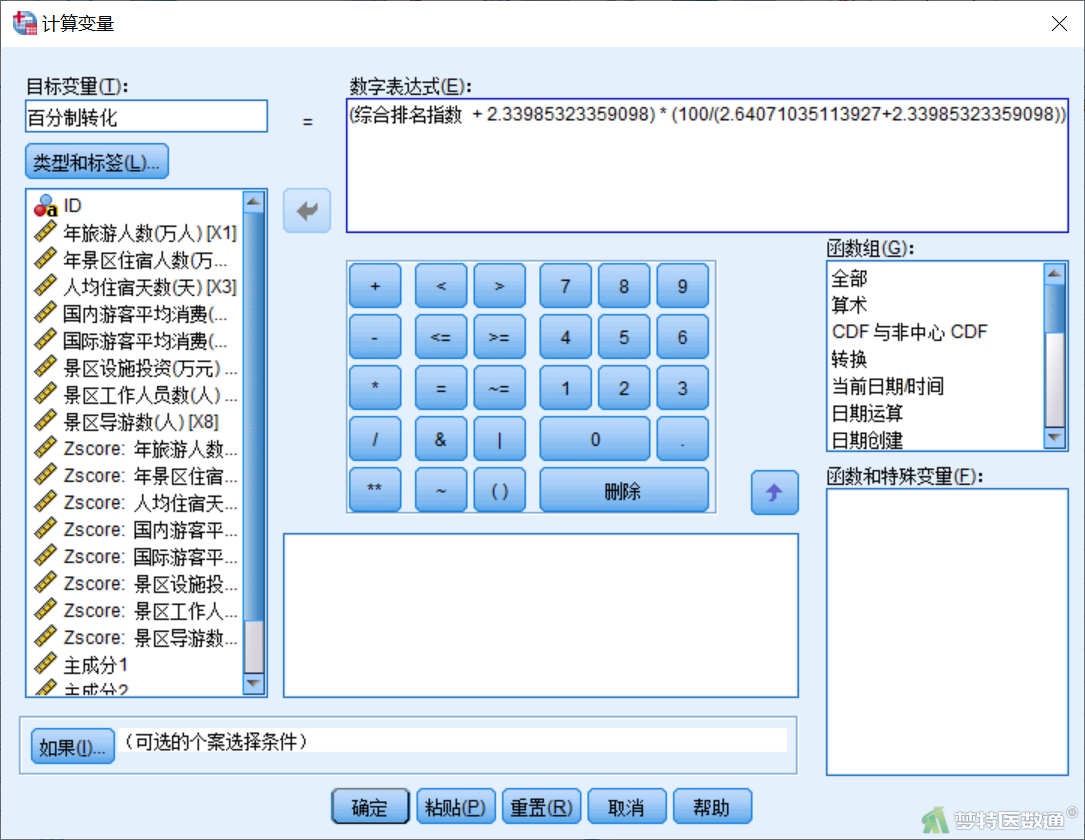
由上述方法计算的综合排名指数是对数据进行标准化后进行的分析，得分处于-3~3之间，如本案例处于-2.33985323359098和2.64071035113927之间。但一般大家习惯使用百分制进行排名，可将综合排名指数转换为百分制。

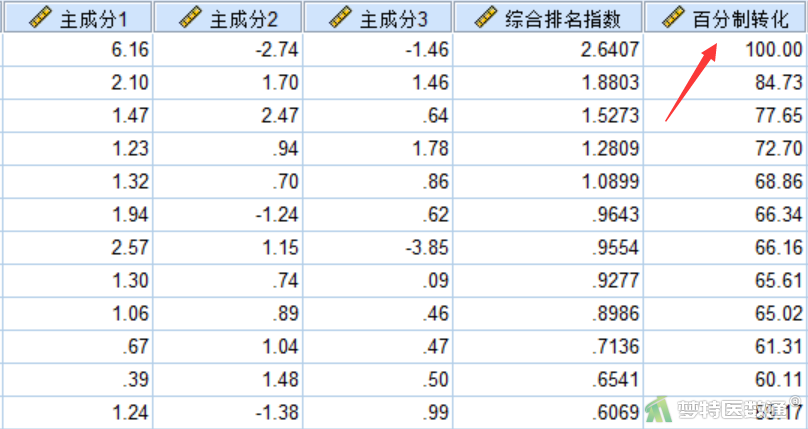
选择“转换”—“计算变量”，目标变量中输入“百分制转换”，数字表达式中输入“(综合排名指数 + 2.33985323359098) * (100/(2.64071035113927+2.33985323359098))”(图9)，即可生成各景区综合排名指数的百分制数值(图10)。