主成分回归法是处理共线性的主要方法之一,可对多个自变量先进行主成分分析,提取出相互独立的主成分,然后再用主成分进行线性回归分析。本文实例演示在SPSS软件中实现主成分回归的操作步骤。
关键词:主成分分析; 多元统计分析; 共线性; 主成分回归
在多因素回归分析中,若需将多个存在多重共线性的自变量引入回归方程,由于共线性的存在,直接建立的回归方程具有不稳定性,严重时可能导致正规方程系数矩阵为奇异矩阵,从而无法求得回归系数。若采用逐步回归,则不得不删除一些自变量。此时可采取主成分回归分析的方法解决多重共线性的问题。
主成分回归是先对多个自变量做主成分分析,综合出少数几个主成分,然后以这几个主成分为自变量与因变量建立回归方程。此时,作为自变量的各主成分互不相关,保证了回归方程的稳定性,也减少了回归分析中自变量的个数。同时,由于主成分是多个原始变量的线性组合,因此通过主成分建立的回归方程也可视为因变量与各原始自变量之间的回归方程。这样就可以把存在多重共线性的多个自变量引入回归方程。
一、案例介绍
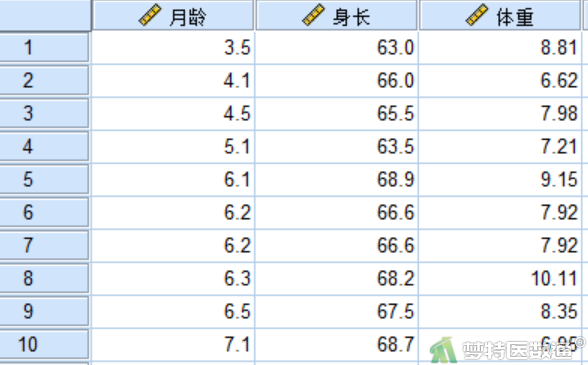
某研究了解婴幼儿体重与月龄和身长的关系,随机测量了60名婴幼儿的月龄(月)、身长(cm)、体重(kg),建立体重与月龄、身长的回归方程。数据见图1。本文案例可从“附件下载”处下载。
二、多重线性回归分析
先建立体重与月龄、身长的多重线性回归方程,具体操作详见“多重线性回归分析(Multiple Linear Regression Analysis)——SPSS软件实现”。分析结果见图2:

可得到回归方程为:
体重 = -12.741-0.117月龄+0.324身长
图2显示两个自变量和常数项的显著性P值均<0.05,具有统计学意义。但是方程中月龄的系数为负值,表示月龄越大体重越低,这与专业不符。观察原因可发现自变量间存在共线性的问题(图3,详见知识小贴士),计算月龄和身长的相关系数高达0.873 (P<0.001)。
三、计算主成分
(一) 主成分分析
选择“分析”—“降维”—“因子”(图4)。

在“因子分析”对话框,将“月龄”、“身长”选入“变量”对话框(图5)。
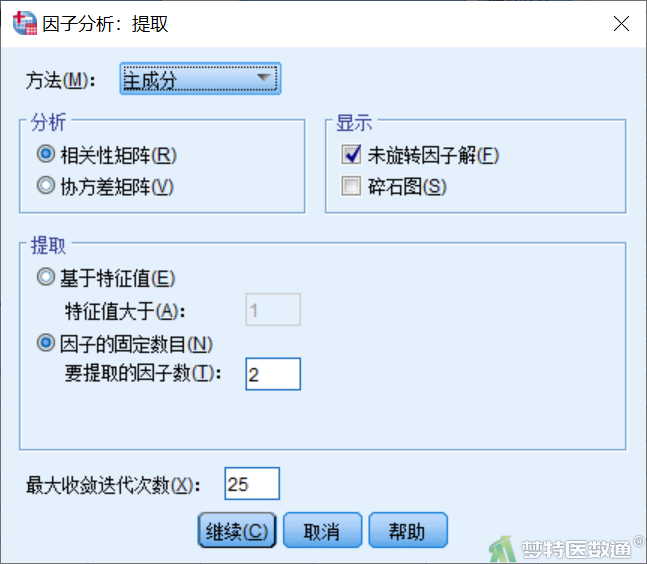
点击“提取”,在“因子分析:提取”页面,方法选择“主成分”,要提取的因子数设置为“2”(图6)。
由图7可知提取了2个主成分,特征值分别为1.873和0.127,其中第一个主成分的贡献率占了93.633%,因此以第一个主成分为自变量构建方程即可。
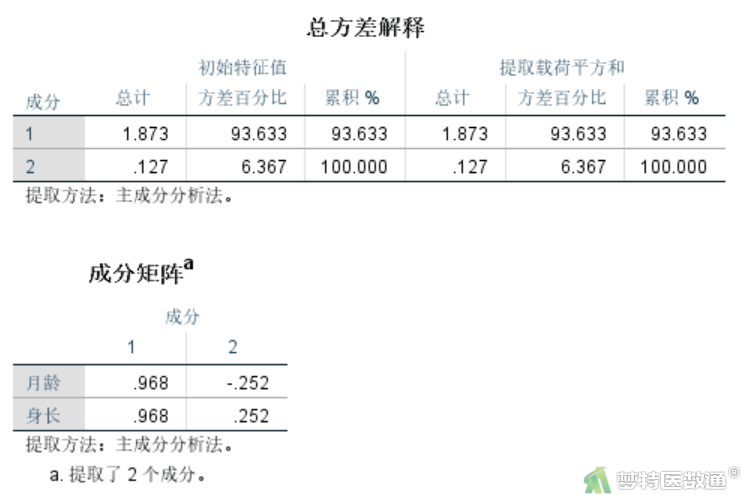
(二) 计算主成分系数
主成分系数计算公式如下:\(\text { 主成分系数 }=\frac{\text { 因子载荷 }}{\sqrt{ } \text { 特征值 }}\),可计算主成分1在月龄上的系数为0.968/sqrt(1.873)=0.707;同理可计算主成分1在身长上的系数为0.968/sqrt(1.873)=0.707。
(三) 原始数据标准化
因为主成分分析过程中各个变量数值均被进行了标准化,因此其主成分计算也需要使用标准化后的变量带入公式。选择“分析”—“统计描述”—“描述”,将2个变量选入右侧“变量框”,勾选“将标准化值另存为变量”(图8),在数据视图页面即可生成2个变量的标化变量。
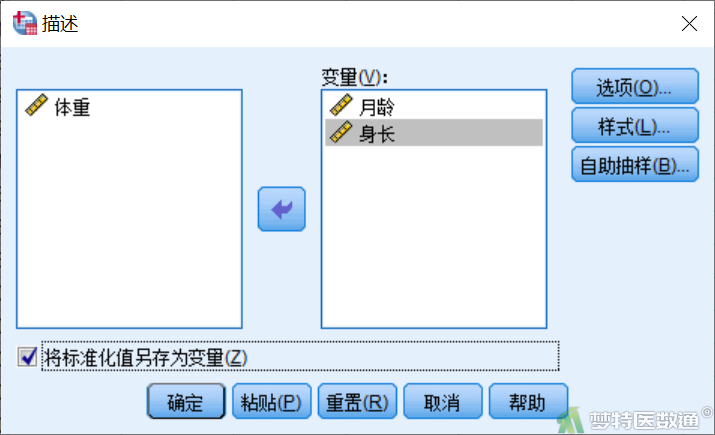
(四) 计算主成分
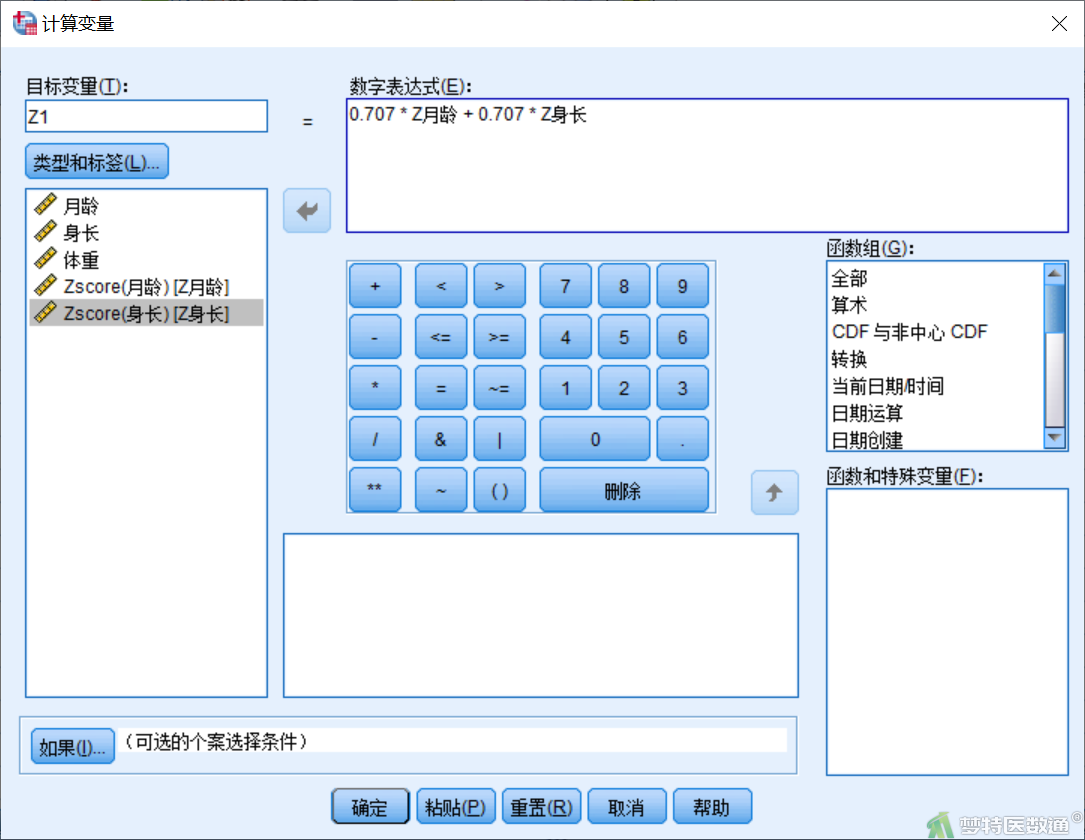
主成分计算公式为主成分系数乘以标准化后的变量,如图9为计算主成分1(Z1)的过程。
主成分方程为:Z1 = 0.707*Z月龄 + 0.707*Z身长
其中Z月龄和Z身长分别是月龄和身长标准化后的变量。
四、主成分回归
(一) 主成分回归
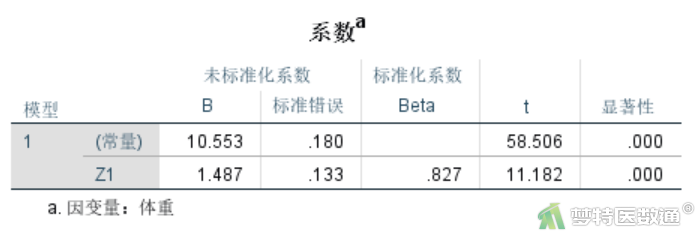
以体重为因变量,以主成分1 (Z1)为自变量,建立线性回归方程,分析结果如图10所示。
可得到回归方程为:
体重 = 10.553+1.487*Z1
(二) 还原回归方程
将Z1 = 0.707*Z月龄 + 0.707*Z身长,带入方程:体重 = 10.553+1.487*Z1,可得:
体重 = 10.553+1.487*(0.707*Z月龄 + 0.707*Z身长)
上式中,
Z月龄=(月龄-月龄mean)/S月龄,Z身长=(身长-身长mean)/S身长
可计算:月龄mean =13.525,S月龄=5.933,身长mean =76.673,S身长=8.612
将相关数值带入:体重 = 10.553+1.487*(0.707*Z月龄 + 0.707*Z身长),可最终计算得到方程为:
体重 = -1.203+0.177月龄+0.122身长
可见,在新的回归方程中,月龄的系数变为了正号。通过主成分回归,虽然丢弃了原始自变量6.367%的信息,但所得到的回归方程更加符合实际。
五、知识小贴士
(一) 多重共线性的判断
除了在“二分类logistic回归分析(Binomial Logistic Regression Analysis)——SPSS软件实现”一文中介绍的多重共线性的判断方法以外,还可根据以下原则判断变量之间的多重共线性。
- 一般而言,共线性的识别可以直接依据偏回归系数是否符合专业知识来加以判断,如果出现如本案例中月龄偏回归系数的异常情况,则高度怀疑存在共线性。
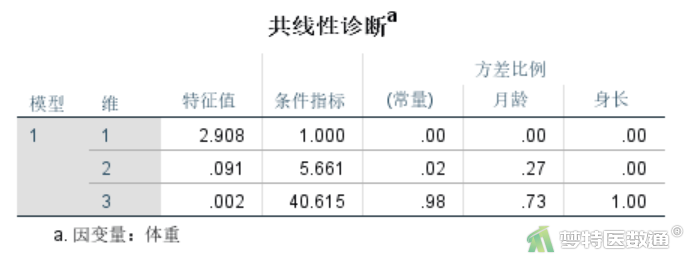
- 特征值(eigenvalue)。对模型中常数项及所有自变量提取主成分,如果自变量间存在较强的线性相关关系,则前面的几个主成分数值较大,而后面的几个主成分数值较小,甚至接近0。如本案例图3中,第1个主成分的特征值为2.908,而第2个主成分的特征值只有0.091,第3个主成分的特征值甚至只有0.002。
- 条件指数(condition index)。即图3中的条件指标,它等于最大的主成分与当前主成分的比值的算术平方根,所以第一个主成分对应的条件指数总为1。如果几个条件指数较大(如大于30),则提示存在多重共线性。图3中第3个主成分的条件指数高达40.615。
- 方差比例(variance proportion)。即变异构成,回归模型中各项(包括常数项)的变异能被各主成分解释的比例,也就是各主成分对模型中各项的贡献。如果某个主成分对两个或多个自变量的贡献均比较大(如大于50%),如本案例主成分3对月龄和身长的贡献比例分别为73%和100%,则说明这两个自变量间存在一定程度的共线性。
(二) 主成分提取个数
主成分回归分析过程中具体提取多少个主成分,需要根据实际情况灵活确定,最好先进行预分析,但提取的主成分不能超过变量个数。