为了能够充分有效地利用数据,可用较少的新指标代替原来较多的旧变量,同时要求这些新指标尽可能地反映原始变量的信息。主成分分析(Principal components analysis, PCA)是解决此问题的有效的多元统计分析方法之一,可以达到提取变量信息、减少分析维度的目的。本文实例演示在SPSS软件中进行主成分分析的操作步骤。
关键词:SPSS; 主成分分析; PCA; 降维; 多元统计分析
一、案例介绍
某研究获得某省份30个景区旅游竞争力评价指标,具体如下:年旅游人数(万人)、年景区住宿人数(万人)、人均住宿天数(天)、国内游客平均消费(元)、国际游客平均消费(元)、景区设施投资(万元)、景区工作人员数(人)、景区导游数(人)。请利用主成分分析找出几个主成分,以便进一步对景区旅游竞争力进行综合评价。
定义变量,将年旅游人数(万人)、年景区住宿人数(万人)、人均住宿天数(天)、国内游客平均消费(元)、国际游客平均消费(元)、景区设施投资(万元)、景区工作人员数(人)、景区导游数(人),分别定义为X1,X2,X3,X4,X5,X6,X7,X8。部分数据见图1。本文案例可从“附件下载”处下载。
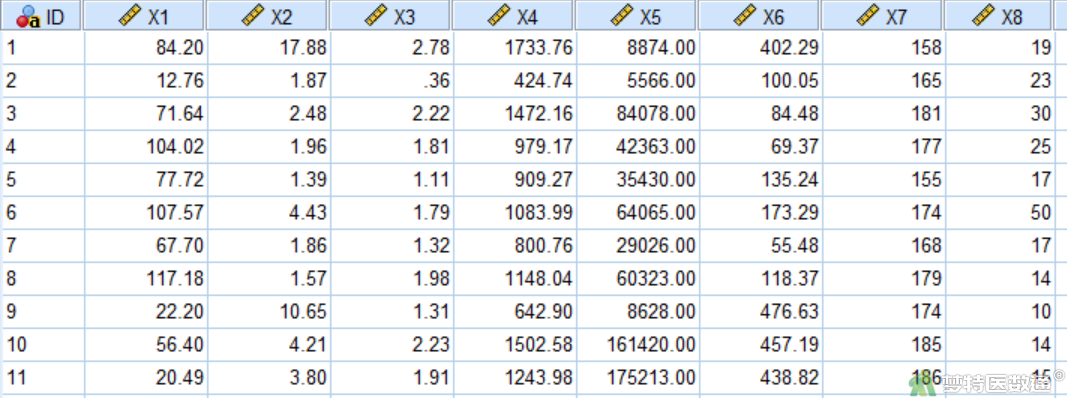
二、问题分析
本案例需要将众多变量归纳为几个有代表性的部分,进行后续分析,可考虑使用主成分分析。主成分分析需要变量间存在一定相关性,可用抽样适合性检验(Measure of Sampling Adequacy, KMO)和Bartlett球形检验进行判断。
三、软件操作及结果解读
(一) 主成分分析
1. 数据标准化
SPSS在进行主成分分析时,会自动首先对数据进行标准化处理,分析输出的结果一般都是标准化的结果。因此无需单独对数据进行标准化处理。
2. 主成分分析
(1) 软件操作
依次点击“分析”—“降维”—“因子”(图2),将X1-X8八个变量选入变量框中(图3)。
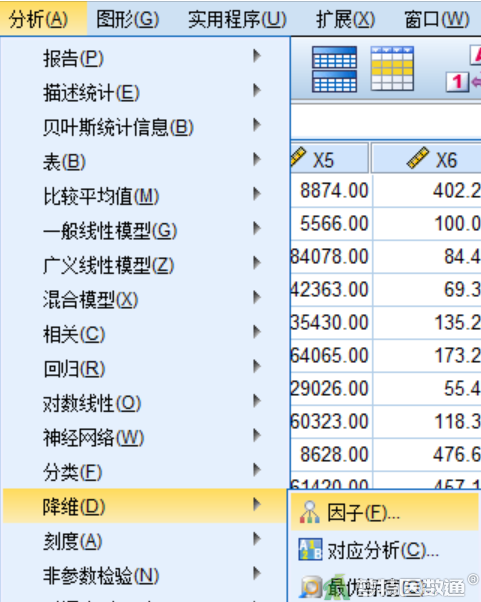
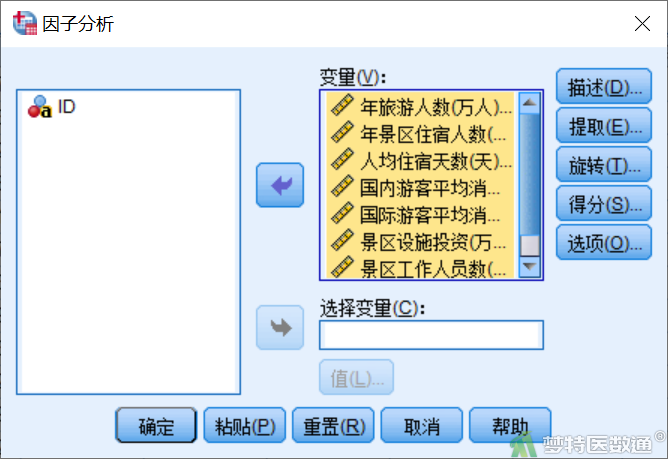
在“因子分析:描述”界面,补充勾选系数和“KMO和巴特利特球形度检验”,后者能够检验该数据是否适合做PCA分析(图4)。
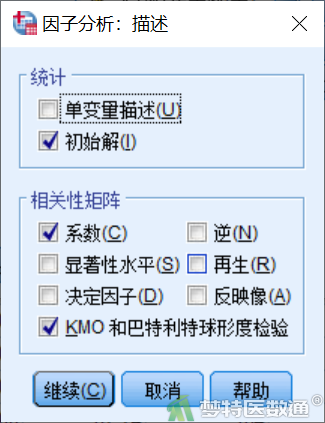
在“因子分析:提取”界面,方法选择“主成分”(此处不能选择其他方法,否则就不是主成分分析),输出默认“未旋转因子解”,补充勾选“碎石图”,提取标准默认“基于特征值大于1”(图5)。
返回到“因子分析”界面,点击“确定”。
(2) 结果解读
图6为变量的相关性矩阵,对于主成分分析,变量间的相关性越高,越适合进行提取主成分。
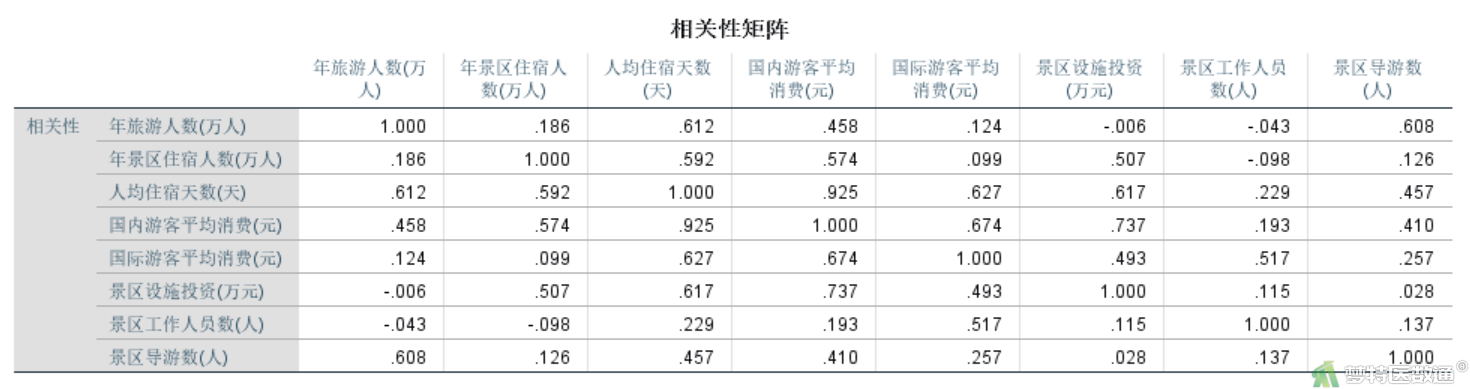
KMO=0.649>0.5,Bartlett球形检验P<0.05 (图7),表明该样本数据适合做主成分分析。

图8为公因子方差,表示对于信息为1的变量,进行主成分提取,每个变量能够被提取的信息比例,此处每个变量的公因子方差均>0.7,表示信息提取较好。
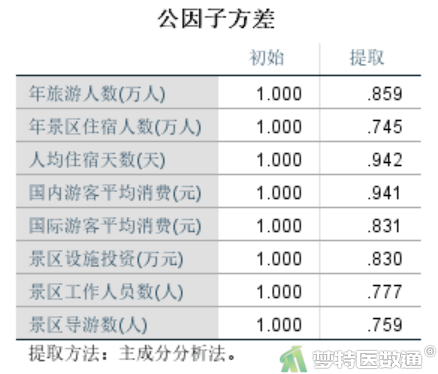
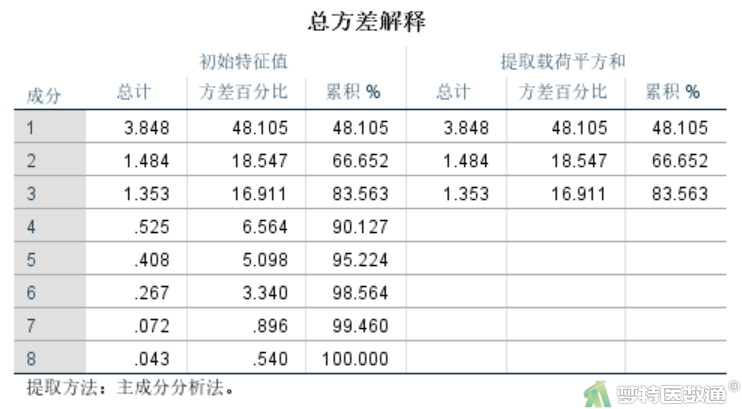
图9为总方差解释结果,表示提取的主成分能够解释总体的信息比例。基于特征值>1的标准,系统提取出了3个主成分,成分1、2、3的特征值分别为3.848、1.484、1.353,三者共可解释总变异的83.563%。尽管离85%还差一点,但是已经很接近该水平,此处可提取3个主成分。当然,如果专业需要,此处也可以提取4个主成分,可达到90.127%的解释率,这并不是严格不变的。
碎石图(Scree plot)用以显示各因子重要性程度,其横轴为因子序号,纵轴表示特征根大小,可以用来协助判断提取的公因子是否合适。通过观察图10碎石图可以看出,碎石图的“肘部”大致位于第三个主成分的位置,往后趋于平缓(且特征值均<1),所以提取三个主成分较为合适。
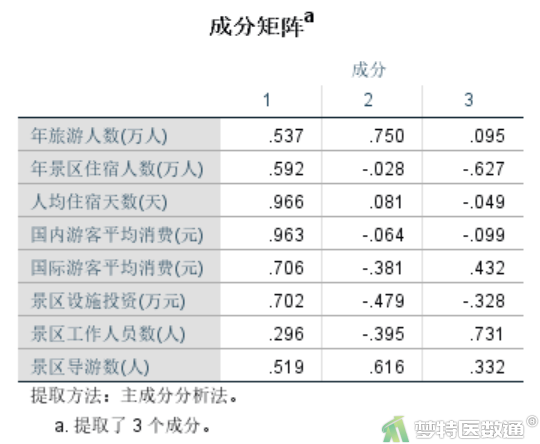
图11为成分矩阵,反映了各因子在各变量上的载荷,即各因子对各变量的影响程度。但此处成分矩阵并不是成分系数,对于成分系数需要进一步计算。
(三) 主成分计算
1. 赋值因子载荷
新建一个SPSS空白数据集,将图11成分矩阵数据复制到空白数据集,命名为因子载荷1、因子载荷2、因子载荷3 (图12)。
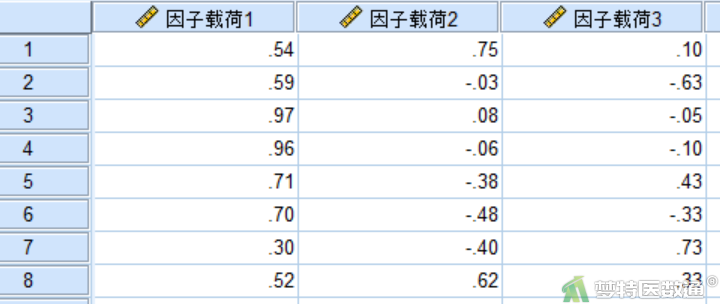
2. 计算主成分系数
主成分系数计算公式如下:\(\text { 主成分系数 }=\frac{\text { 因子载荷 }}{\sqrt{ } \text { 特征值 }}\)
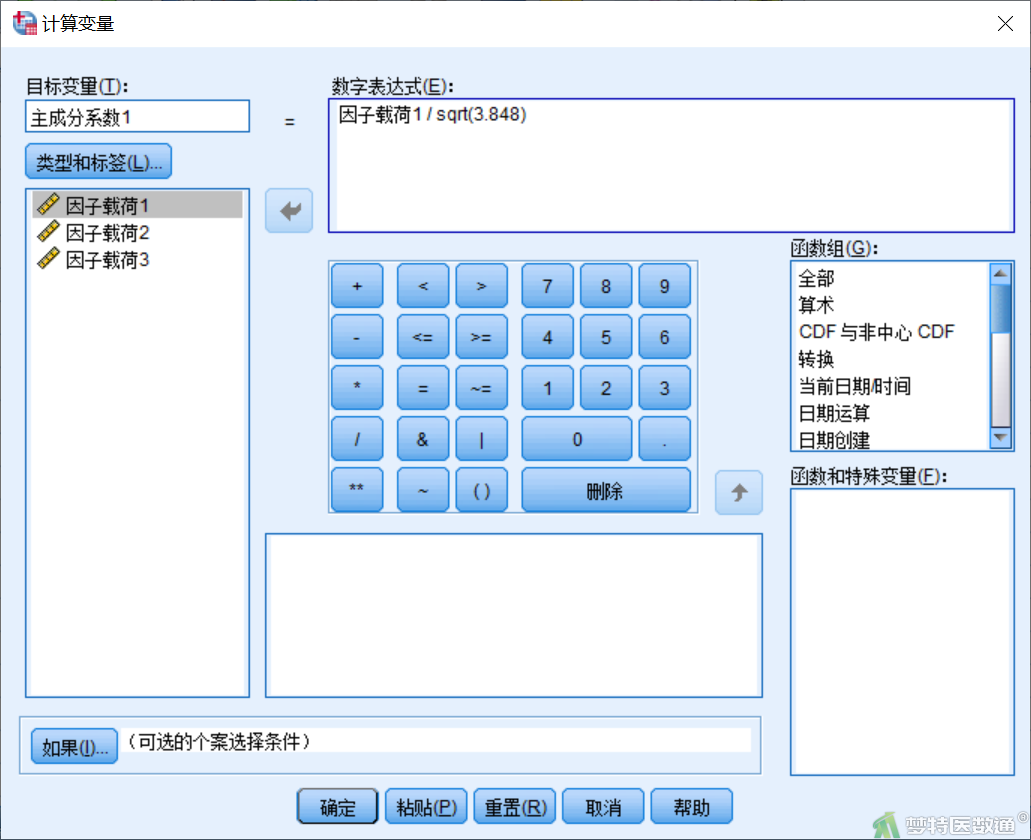
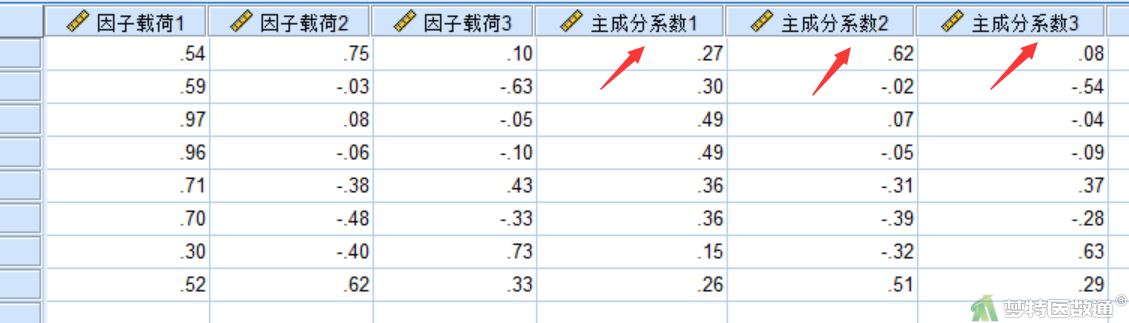
点击“转换”—“计算变量”,目标变量中输入“主成分系数1”,数字表达式中输入“因子载荷1/sqrt(3.848)”(图13),即可生成各个变量在主成分1中的系数。依次操作生成三个主成分的系数,结果如图14所示。
3. 原始数据标准化
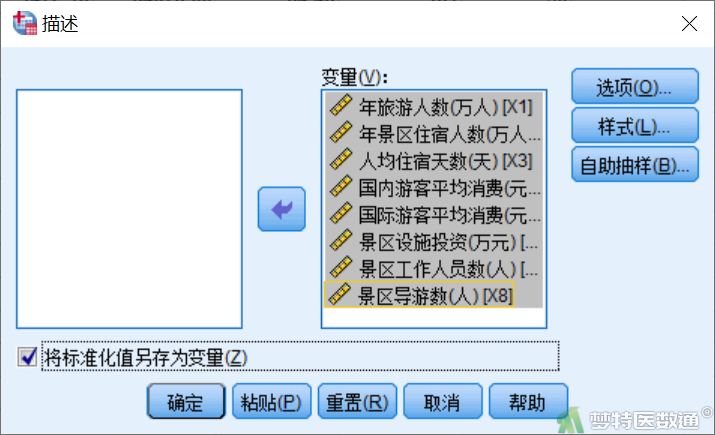
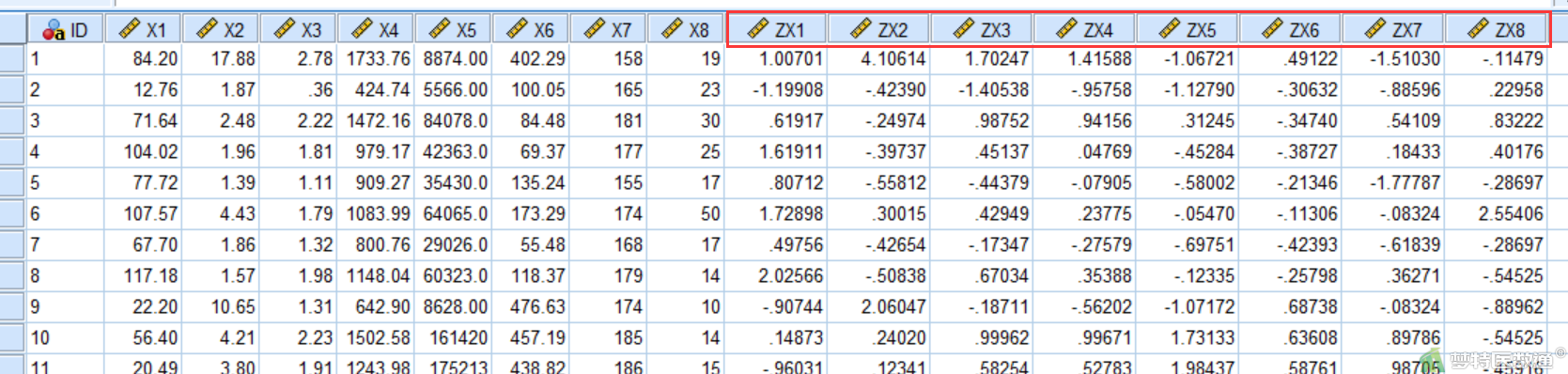
因为主成分分析过程中各个变量数值均被进行了标准化,因此其主成分计算也需要使用标准化后的变量带入公式。选择“分析”—“统计描述”—“描述”,将八个变量选入右侧“变量框”,勾选“将标准化值另存为变量”(图15),在数据视图页面即可生成8个变量的标化变量(图16)。
4. 计算主成分
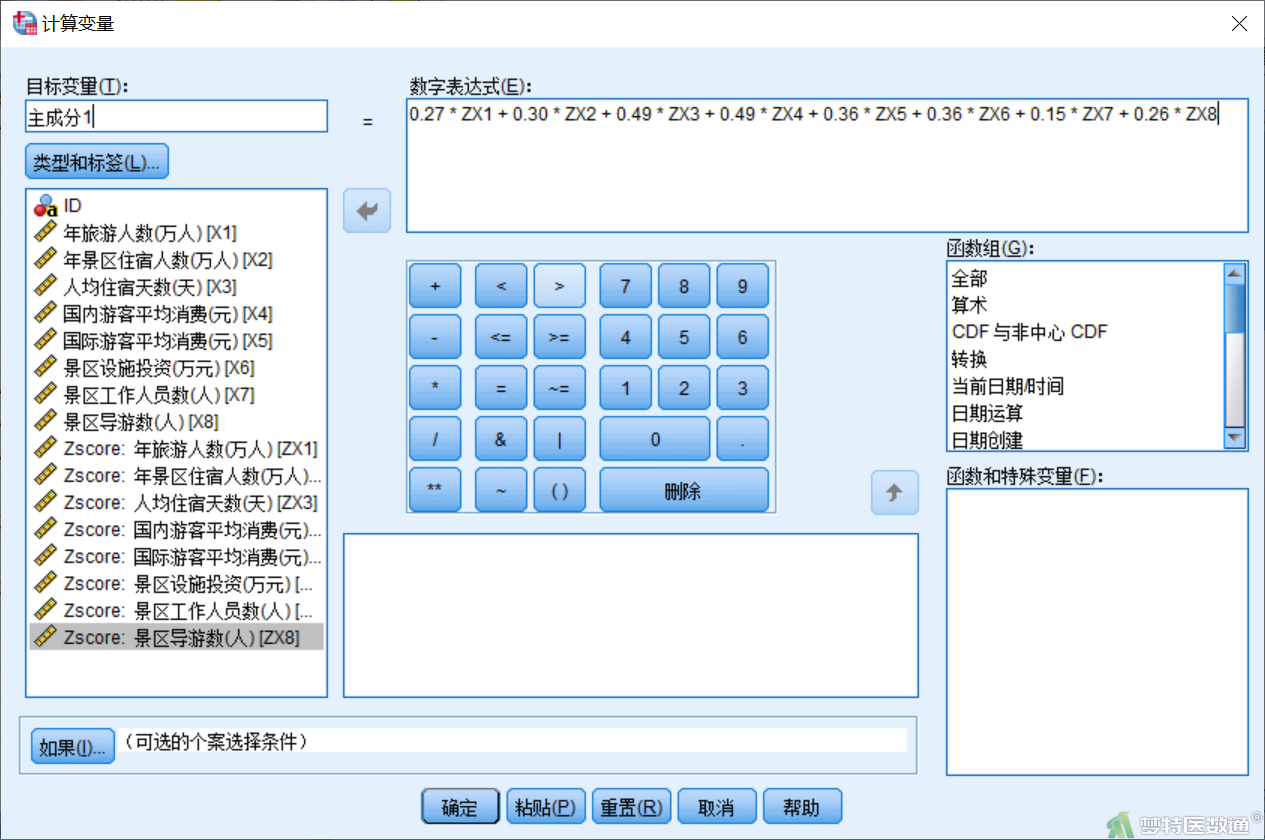
主成分计算公式为主成分系数乘以标准化后的变量,如图17为计算主成分1的过程,依次可计算主成分2和主成分3,结果如图18所示。
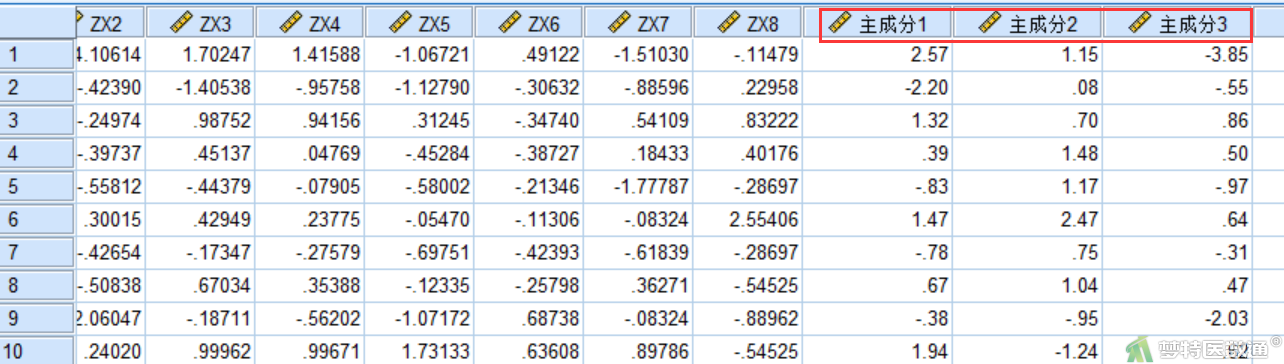
据此可写出主成分的计算公式:
主成分1 = 0.27×ZX1+0.30×ZX2+0.49×ZX3+0.49×ZX4+0.36×ZX5-0.36×ZX6+0.15×ZX7+0.26×ZX8
主成分2 = 0.62×ZX1-0.02×ZX2+0.07×ZX3-0.05×ZX4-0.31×ZX5-0.39×ZX6-0.32×ZX7+0.51×ZX8
主成分3 = 0.08×ZX1-0.54×ZX2-0.04×ZX3-0.09×ZX4+0.37×ZX5-0.28×ZX6+0.63×ZX7+0.29×ZX8
第一主成分中各个变量的系数绝对值均较大,因此第一主成分应当是反映景区旅游竞争力的综合指标。第二主成分中年旅游人数(万人)、景区导游数(人)的系数绝对值较大,应当是反应导游相关的旅游总人数方面的综合指标。第三主成分中年景区住宿人数(万人)、景区工作人员数(人)的系数绝对值较大,应当是反应工作人员、和留宿旅游人数方面的综合指标。
四、知识小贴士
- KMO系数是抽样适合性检验的系数,该检验是对原始条目之间的简单相关系数和偏相关系数的相对大小进行检验,如果原始数据中确实存在公因子,则各条目之间的偏相关系数应该很小,这时KMO值接近于1,因此,数据适合于因子分析。该指标的最低标准为0.5,0.5~0.7为勉强适合,0.7~0.8为适合,0.8~0.9为很适合,>0.9为非常适合。
- Bartlett检验的零假设是研究数据之间的相关矩阵是一个完美矩阵,即所有对角线上的系数为1,非对角线上的系数均为0。在这种完美矩阵的情况下,各条目之间没有相关关系,即不能将多个条目简化为少数的成分,没有进行探索性因子分析的必要。因此希望拒绝Bartlett检验的零假设。