因子分析的核心思想是寻找公因子,以达到降维的目的,探索性因子分析和验证性因子分析是其两大主要类型。探索性因子分析(Exploratory factor analysis, EFA)主要是为了初步找出因子个数以及因子下各个观测变量的组成、相关程度,以进一步为改进因子结构提供依据。在量表的效度评价中,探索性因子分析和验证性因子分析较为常用。本文实例演示在SPSS软件中进行探索性因子分析的操作步骤。
关键词:SPSS; 主成分分析; 探索性因子分析; 验证性因子分析; 多元统计分析
一、案例介绍
使用一份心理人格量表调查了250名受试者,所用量表包含A1~A5(其中A1为反向条目)、C1~C5(其中C4、C5为反向条目)、E1~E5(其中E1、E2为反向条目)、N1~N5,O1~O5(其中O2、O5为反向条目),5个维度(A、C、E、N和O)共25个条目。现希望使用探索性因子分析对此份量表数据的结构效度进行分析,并对量表进行改进。部分数据见图1。本案例数据可从“附件下载”处下载。
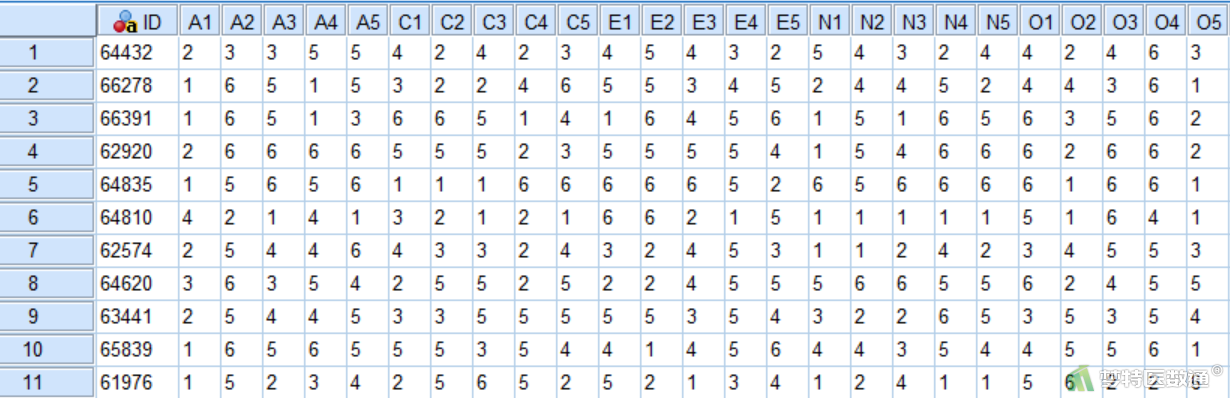
二、问题分析
由于本研究的量表是一个初步量表,已经初步设置了5个维度及其相应的条目,因此分析时最好选用探索性因子分析,并且固定因子数目为5。但需要满足四个条件:
条件1:数据是以量表形式进行整理和呈现的,对于非量表类数据不合适。本研究是一个初步量表,并设置了相应维度和对应的条目,该条件满足。
条件2:样本例数>分析条目数的5倍,总样本通常不低于100。本研究25个条目,其5倍数量为125,总样本250满足该条件。
条件3:Kaiser-Meyer-Olkin (KMO)系数≥0.6。该条件需要通过软件分析后判断。
条件4:巴特利特球形度检验有统计学意义(P<0.05)。该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 数据整理
由于条目中存在反向计分条目,为了后续计算、结果解读的方便,在进行数据分析之前先将反向计分条目进行转换。
①选择“转换”—“重新编码为不同变量”(图2);将需要进行反向编码的“A1”变量拖入到“数字变量->输出变量”框中,表示需要对条目“A1”进行转换;对反向编码的变量进行命名,表示转换成一个新的条目,在“输入变量”框中的“名称”项中输入“A1r”,表示新条目的名字,点击“变化量”(图3)。
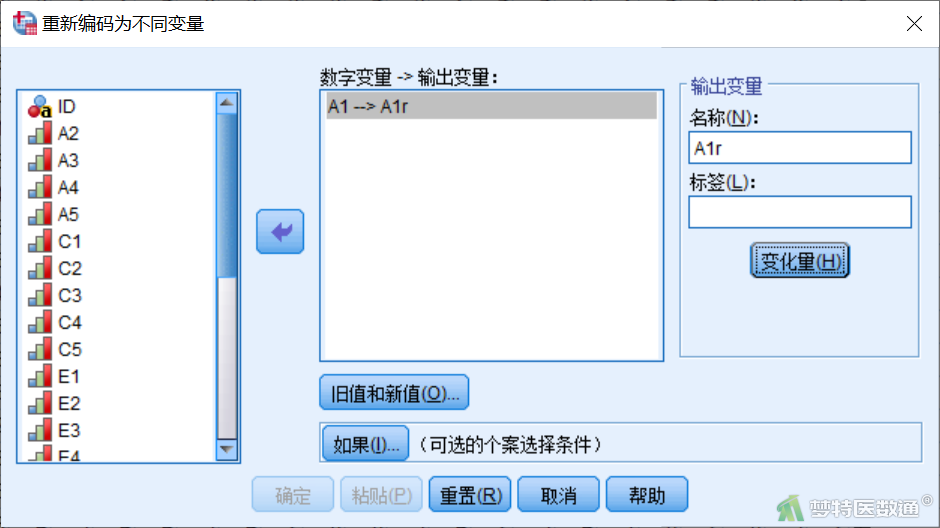
②点击“旧值和新值”,打开“重新编码为不同变量:旧值和新值”框,在“旧值”框中的“值”项中输入“6”,在“新值”框中的“值”项中输入“1”,表示将条目中的“6”替换为“1”;点击“添加”,其余以此类推(图4);点击“继续”,点击“确定”。
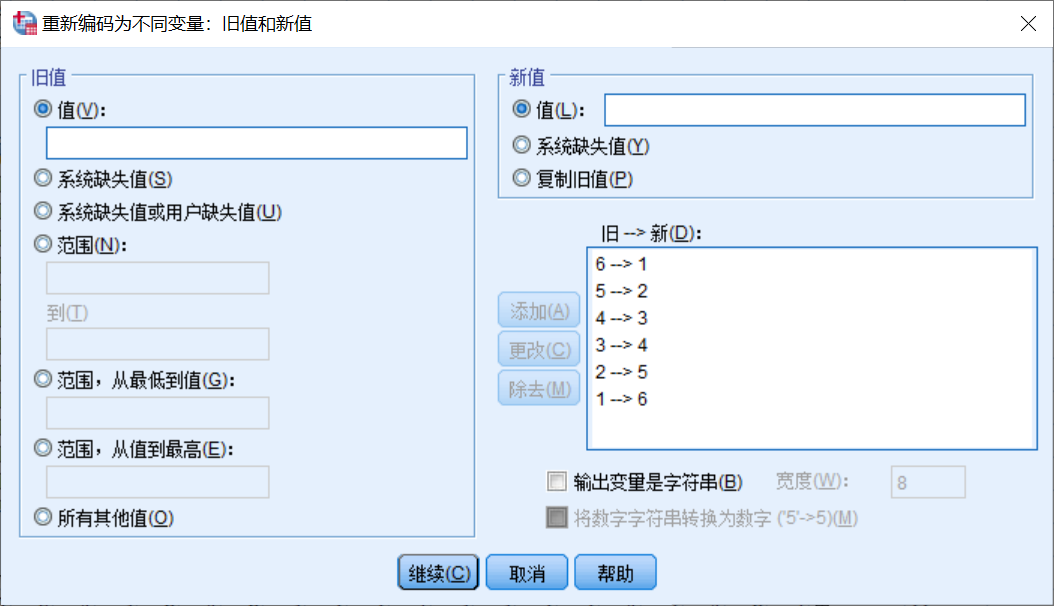
③此时在数据集中生成了一列新的条目“A1r”(图5),是反向计分条目“A1”的正向计分条目。

④以此类推对其余反向计分条目进行转换。
(二) 适用条件判断
条件3和条件4判断。
1. 软件操作
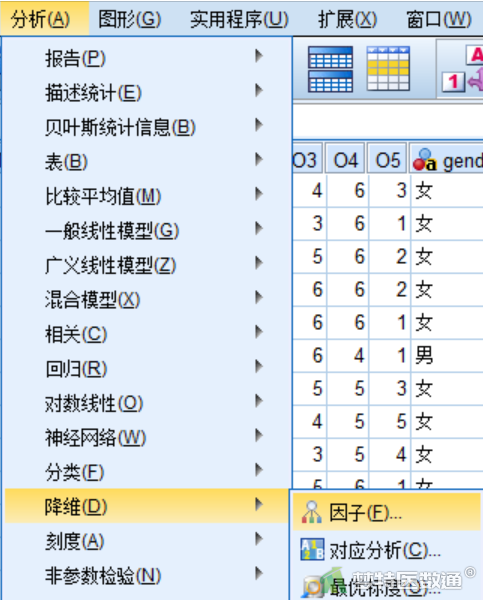
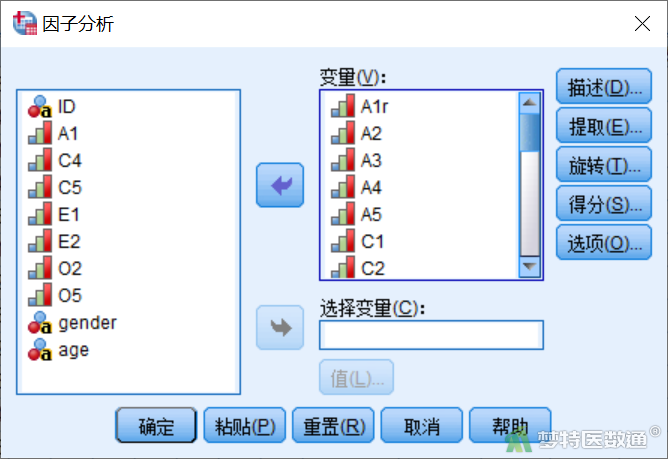
①选择“分析”—“降维”—“因子”(图6),将需要分析的25个条目(反向计分条目需要选择转换后的条目)选入右侧“变量”框(图7)。
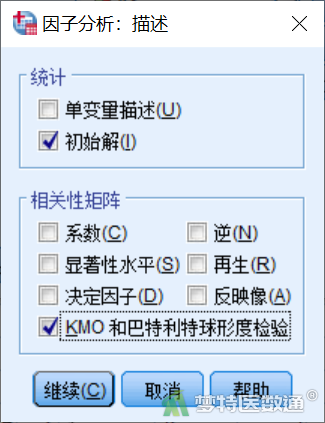
②点击“描述”,勾选“相关性矩阵”框中的“KMO和巴特利特球形度检验”,点击“继续”(图8)。
③点击“提取”,在“显示”框中补充勾选“碎石图”,在“提取”框中的“因子的固定数目”—“要提取的因字数”中输入“5”,点击“继续”(图9),点击“确定”,结果如表1所示。


2. 结果解读
表1“KMO和巴特利特检验”表格中,KMO系数为0.808,提示数据抽样充分,结构很适合进行因子分析。巴特利特球形度检验的近似卡方为2204.278,P<0.001,拒绝零假设,提示数据结构适合进行因子分析。
KMO系数是抽样适合性检验(Measure sampling adequacy)的系数,该检验是对原始条目之间的简单相关系数和偏相关系数的相对大小进行检验,如果原始数据中确实存在公因子,则各条目之间的偏相关系数应该很小,这时KMO值接近于1,因此,数据适合于因子分析。在因子分析中,该指标的最低标准为0.6,0.6~0.7为勉强适合,0.7~0.8为适合,0.8~0.9为很适合,>0.9为非常适合。
如果分析过程中出现KMO值分析结果报错或不存在的情况可从以下几个方面进行核查和改进:
- 是否存在异常值;
- 是否放入了无序多分类数据进行分析;
- 样本量是否过少,样本量过少容易导致相关系数过高;
- 分析条目之间的相关系数过低或过高:系数过低(比如小于0.2或没有显著性),信息重叠度低无法有效浓缩信息,会导致KMO值较低;系数过高(比如大于0.8),会导致严重共线性,可能无法输出KMO值;分析条目之间的相关系数值介于0.3~0.7之间较好。
巴特利特球形度检验的零假设是研究数据之间的相关矩阵是一个完美矩阵,即所有对角线上的系数为1,非对角线上的系数均为0。在这种完美矩阵的情况下,各条目之间没有相关关系,即不能将多个条目简化为少数的成分,没有进行探索性因子分析的必要。因此希望拒绝巴特利特球形度检验的零假设。
(三) 因子载荷分析
EFA分析最重要的目的就是判断维度和题目对应关系是否与专业预期符合,主要依据就是判断各条目在预期维度上的载荷是否合理。
1. 软件操作
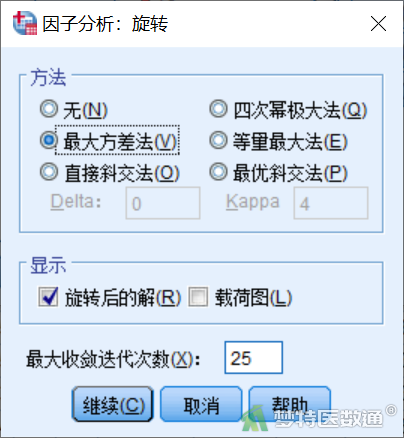
①在“因子分析”对话框中(图7),点击“旋转”,打开“因子分析:旋转”对话框,在“方框”框中选中“最大方差法”项(图10),点击“继续”。
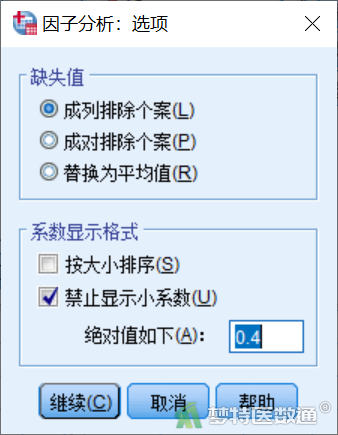
②在“因子分析”对话框中(图7),点击“选项”,打开“因子分析:选项”对话框,在“系数显示格式”中勾选“禁止显示小系数”,在“绝对值如下”右侧填入“0.4”,表示在结果表格中将载荷低于0.4的系数隐藏掉(图11),这样方便阅读;点击“继续”,点击“确定”,结果如表2所示。
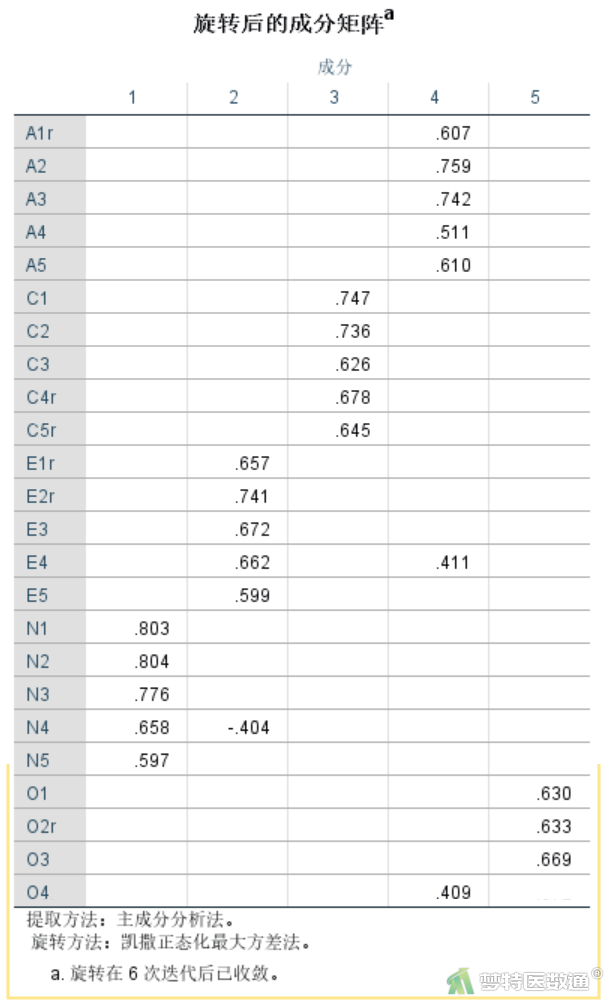
2. 结果解读
表2“旋转后的成分矩阵”结果,列出了各个条目在每个维度上的因子载荷,一般要求>0.4。可见A1r~A5五个条目均在成分4下面,并且系数均>0.4;C1~C5r五个条目均在成分3下面,并且系数均>0.4;E1r~E5五个条目在成分2下面均有载荷>0.4,但E4还在成分4下有一定载荷(0.411),这种现象叫做“混乱不清”;N1~N5五个条目在成分1下面均有载荷>0.4,但N4还在成分2下有一定载荷(-0.404);O1~O5r五个条目中有四个均在成分5下,且载荷>0.4,但O4却落在了成分4下,出现了“错分”的情况。
在EFA分析过程中最重要的就是处理“错分”现象,让条目落在预期专业的维度下面。对于“混乱不清”的现象,则根据具体情况灵活处理。此处,先删除O4条目后重新分析。
3. 改进分析
删除O4条目后重新分析的“旋转后的成分矩阵”结果如表3所示。可见各个条目均在本维度下具有较好的载荷(>0.4),已不存在“错分”的情况。但E4和N4同时在其他成分下面具有较高的载荷(>0.4),存在较为严重的“混乱不清”现象,因此,需要删除E4和N4。
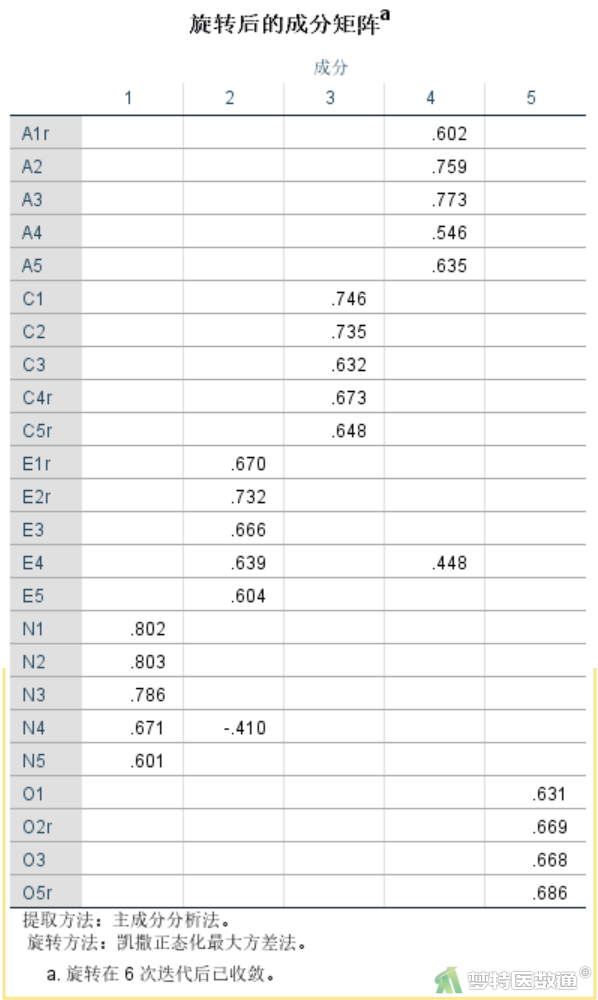
删除E4和N4条目后重新分析的“旋转后的成分矩阵”结果如表4所示。发现O3条目在其他成分3下面仍具有较高的载荷(>0.4),存在较为严重的“混乱不清”现象,因此,需要删除O3。
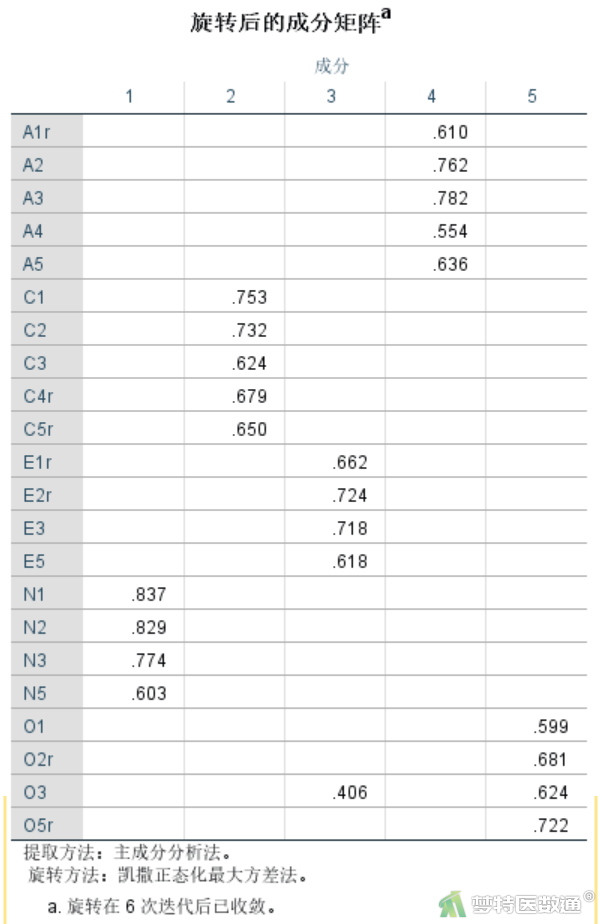
进一步删除O3条目后重新分析因子载荷情况如表5所示。可见各个条目均在本维度下具有较好的载荷(>0.4),已不存在“错分”的情况。
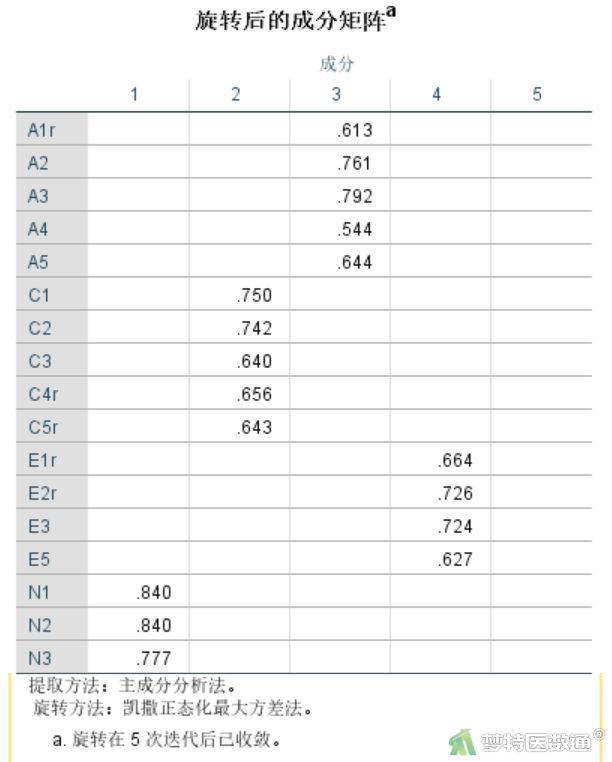
条目出现“错分”和“混乱不清”是EFA分析过程中常见的现象,但最为关注的是“错分”情况,需要优先处理,一般是待处理完条目“错分”情况后再处理“混乱不清”的现象。
对出现“混乱不清”的条目,通常是按照条目落在非预期维度下的载荷系数高低进行逐个删除,一般在非预期维度下载荷系数>0.4的条目先删除。对于在非预期维度下载荷系数<0.4的条目多根据专业意义和条目数量进行综合考虑。如果该条目具有重要的专业意义,必须保留,或者该维度下剩余的条目数不多(如只有3条),则可先予以保留。
(四) 公因子方差
公因子方差反映了提取的主成分对各个条目信息的代表程度,一般要求公因子方差>0.4。
从表6“公因子方差”表格中的“提取”可知,本例数据满足公因子方差的要求。
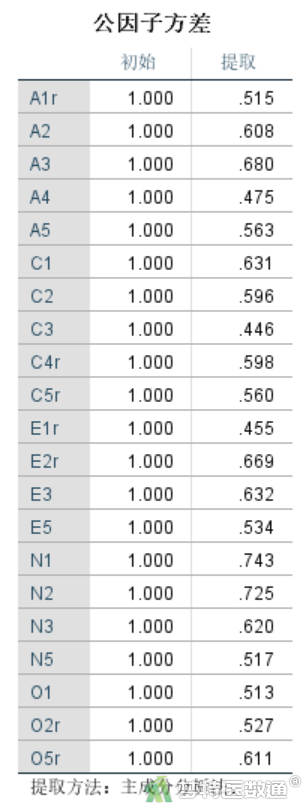
【注意】
- 如果根据公因子方差值进行条目删除,其余条目的公因子方差值会重新计算。因此,要按照公因子方差从大到小的顺序逐个删除。
- 除了考虑公因子方差的大小以外,该条目的专业意义和维度内剩余条目数也需要加以考虑。如果该条目具有重要的专业意义,必须保留,或者该成分下剩余的条目数不多(如只有3条),则可先予以保留。
(五) 方差解释率
EFA分析的主要目的之一是通过选取的主成分因子(维度)对数据进行降维,但同时也要注意应尽可能多的包含对数据变异的解释。
1. 软件操作
在“因子分析”(图7)页面,点击“确定”,输出结果如表7所示。
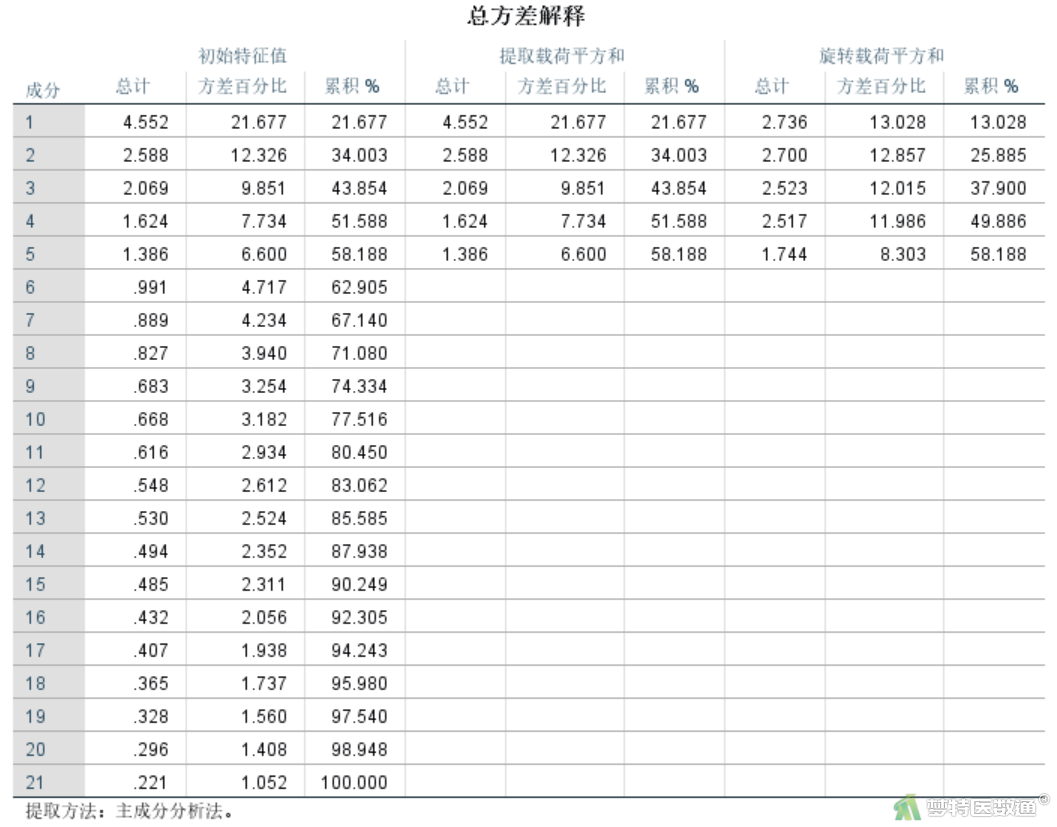
2. 结果解读
在表7“总方差解释”表格中,每个主成分因子(维度)的解释率都>5%,累计方差解释率为58.188%。表明五个维度可以提取的量表信息程度一般,综合说明研究数据结构效度一般。
一般认为,提取的每个主成分因子至少应解释5%~10%的数据变异。关于累计解释率对于不同专业有不同要求,对于医学专业而言,一般要求提取的主成分应累积解释60%~70%的数据变异;对于社会学往往不容易达到较高的比例。此外,在EFA过程中,由于使用的量表可能并非成熟的权威量表,往往总方差解释率不可能达到很高。但对于一个成熟、通用的量表如果累计方差解释率太低则表明数据的结构效度不是很理想。
(六) 其他指标解读
1. 碎石图
在“因子分析:提取”中,勾选“碎石图”(图9),结果如图12所示。
图12“碎石图”以图形化的方式展示了因子的特征值变化,可见前五个因子后迅速变缓,辅助提示提取5个维度较为合适。
2. KMO检验系数和巴特利特球形度检验结果
KMO检验系数和巴特利特球形度检验结果会随着条目的改变而发生变化。本案例分析,最终“KMO和巴特利特球形度检验”结果中,“整体”MSA系数为0.775(表8),提示数据抽样充分,结构很适合进行因子分析。“巴特利特球形度检验”结果中,近似卡方=164.338,P<0.001(表8),提示数据结构适合进行因子分析。

四、结论
本研究采用探索性因子分析方法评估心理人格量表的结构效度情况。初始量表数据结构合理(KMO检验系数为0.808,巴特利特球形度检验结果为P<0.001),提示数据可以进行探索性因子分析。
通过判断条目是否与预期专业维度相匹配删除了O4、E4、N4和O3四个条目,最终保留21个条目构成5个维度。最终量表的KMO检验系数为0.775,巴特利特球形度检验结果为P<0.001。五个维度分别解释13.028%、12.857%、12.015%、11.986%和8.303%的总数据变异,累计解释58.188%的数据变异。综上所述,该研究数据结构效度水平一般。
五、知识小贴士
本文分析结果和探索性因子分析(Exploratory Factor Analysis)——jamovi软件实现并不完全一致。主要是因为选择的提取方法和因子旋转方法不一致所致。
因子分析的解并不唯一:
- 同一问题可以有不同的因子分析解,如主成分解、主因子解、极大似然解等。在处理实际问题时,可根据具体情况选择不同的方法来获得符合客观实际的解。
- 可以通过各种方法进行因子旋转以获得更为满意的解,至于选用何种方法进行因子旋转,也需根据专业意义来确定。如果一次旋转所得结果不够理想,可以用迭代的方法进行多次旋转,直到最后相邻两次旋转所得的因子载荷改变不大时即可停止。
六、分析小技巧
(一) 结构效度分析结果不理想如何处理?
结构效度分析,是综合各项指标进行综合判断,包括KMO检验系数和巴特利特球形度检验结果、因子载荷系数、公因子方差、方差解释率、累积方差解释率等。分析过程中,往往不是一步到位,而是需要删除条目,重复进行多次,以使维度和条目对应关系符合预期,找出最优结果;最为关键的就是使维度和条目对应关系与专业预期符合。
(二) 非量表数据的结构效度不能通过EFA分析。
对于非量表数据的结构效度,往往只需要使用文字描述问卷的设计过程,包括参考依据、问题设计与思路如何保持一致性、是否进行过预测试和专家团队的评估、对问卷进行过哪些修改处理等。