多重线性回归分析(Multiple Linear Regression Analysis)——SPSS软件实现

关键词：SPSS; 多重线性回归; 多元线性回归; 多重共线性; 自变量选择; 逐步回归; 模型拟合评价; 哑变量设置

一、案例介绍

某社区医师从本社区的糖尿病患者中随机抽取50名，收集了他们的性别(Gender，0=女，1=男)、经济水平(Income，1=低收入，2=中等收入，3=高收入)、空腹胰岛素(Fasting insulin，mmol/L)、糖化血清蛋白(Glycosylated serum protein)和空腹血糖(FBS，mmol/L)，欲探究空腹血糖是否受到其它几项指标的影响。部分数据见图1。

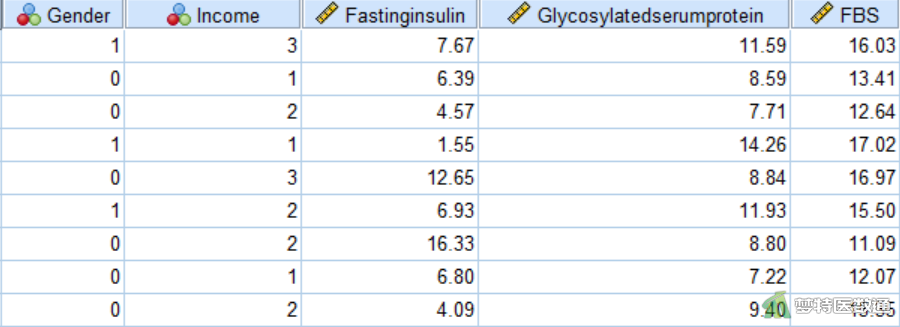
二、问题分析

本案例的目的是分析空腹血糖是否受到其他几项指标的影响，由于因变量是定量资料，初步考虑可使用多重线性回归分析。但需要满足以下7个条件：

条件1：样本量是自变量个数的5~10倍。本案例有4个自变量，样本量为50，满足该条件。

条件2：自变量若为连续变量，需要与因变量之间存在线性关系，可通过绘制散点图予以考察。

条件3：各观测值之间相互独立，即残差之间不存在自相关。通过研究设计和数据收集的过程分析，可判断本案例中观测值之间不存在互相影响的情况。该条件还可通过软件分析后辅助判断。

条件4：不存在显著的多变量异常值，该条件需要通过软件分析后判断。

条件5：自变量之间无多重共线性，该条件需要通过软件分析后判断。

条件6：残差符合正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件7：残差大小不随所有变量取值水平的变化而变化，即方差齐性，可通过绘制残差图进行判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件2判断(线性关系判断)

检验因变量与连续性自变量之间是否存在线性关系，可通过绘制每个自变量和因变量的散点图进行判断。

(1) 软件操作

① 选择“图形”—“图表构建器” (图2)。

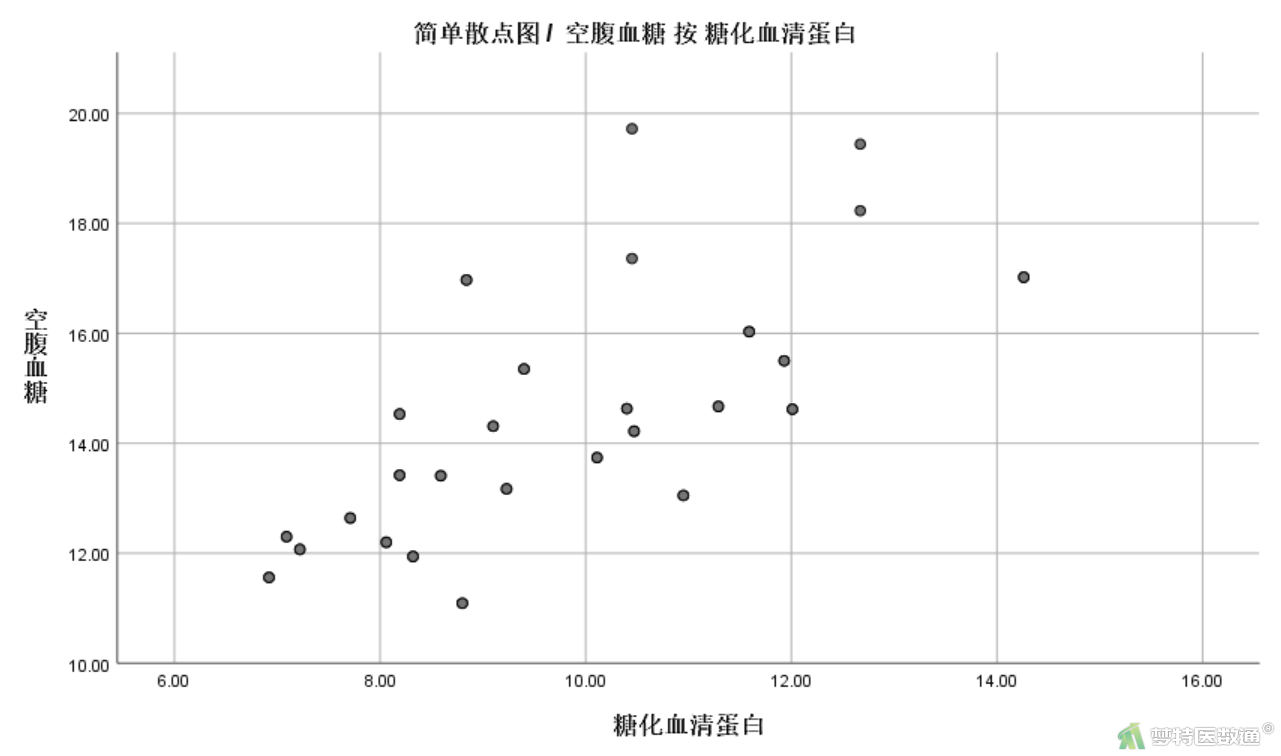
② 在“图表构建器”对话框的“图库”中，选择“散点图/点图”，双击选择“简单散点图”，将自变量“糖化血清蛋白”拖入“X轴”，将因变量“空腹血糖”拖入“Y轴”(图3)。点击“确定”可得到“糖化血清蛋白”与“空腹血糖”之间的散点图如图4所示。

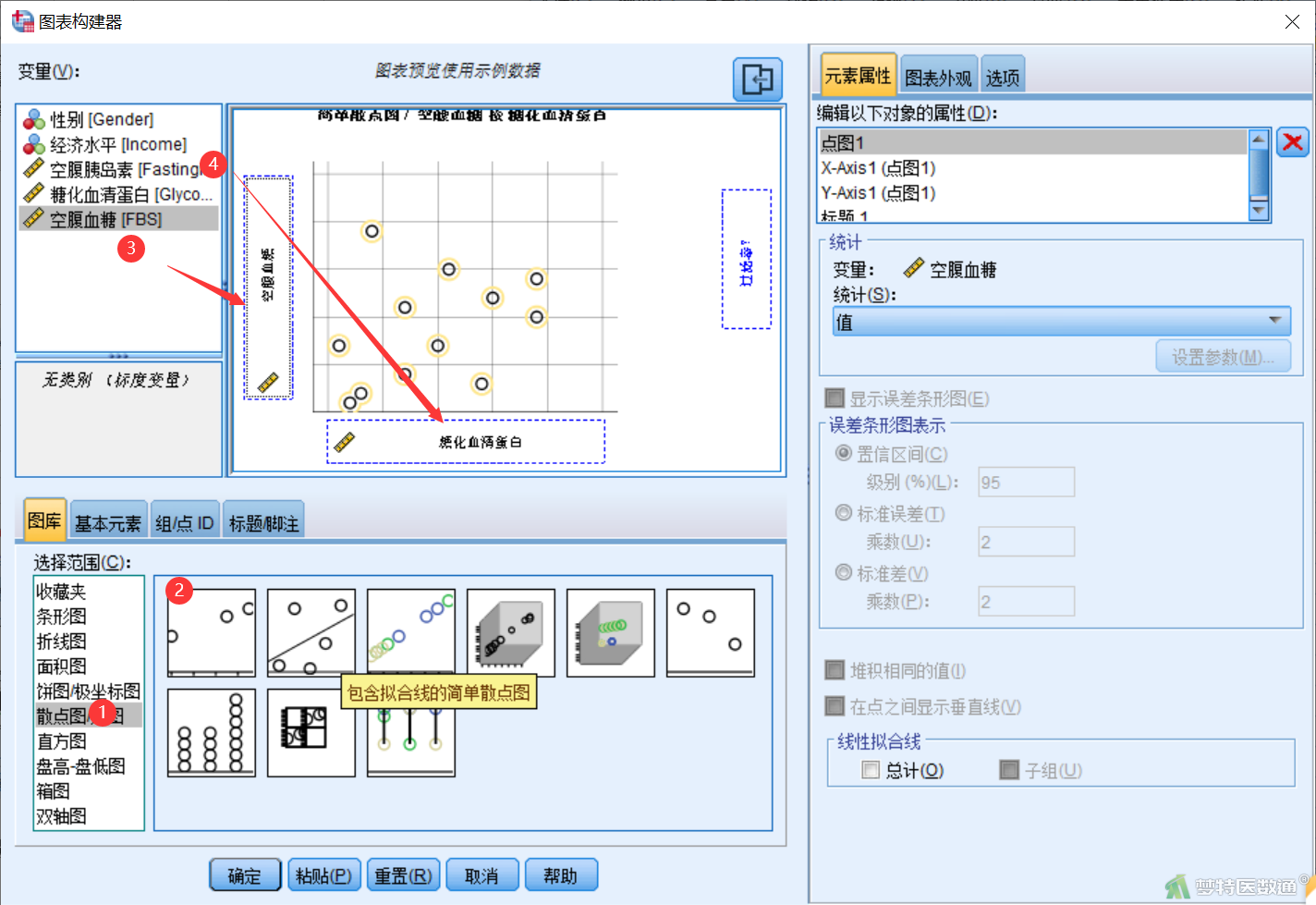
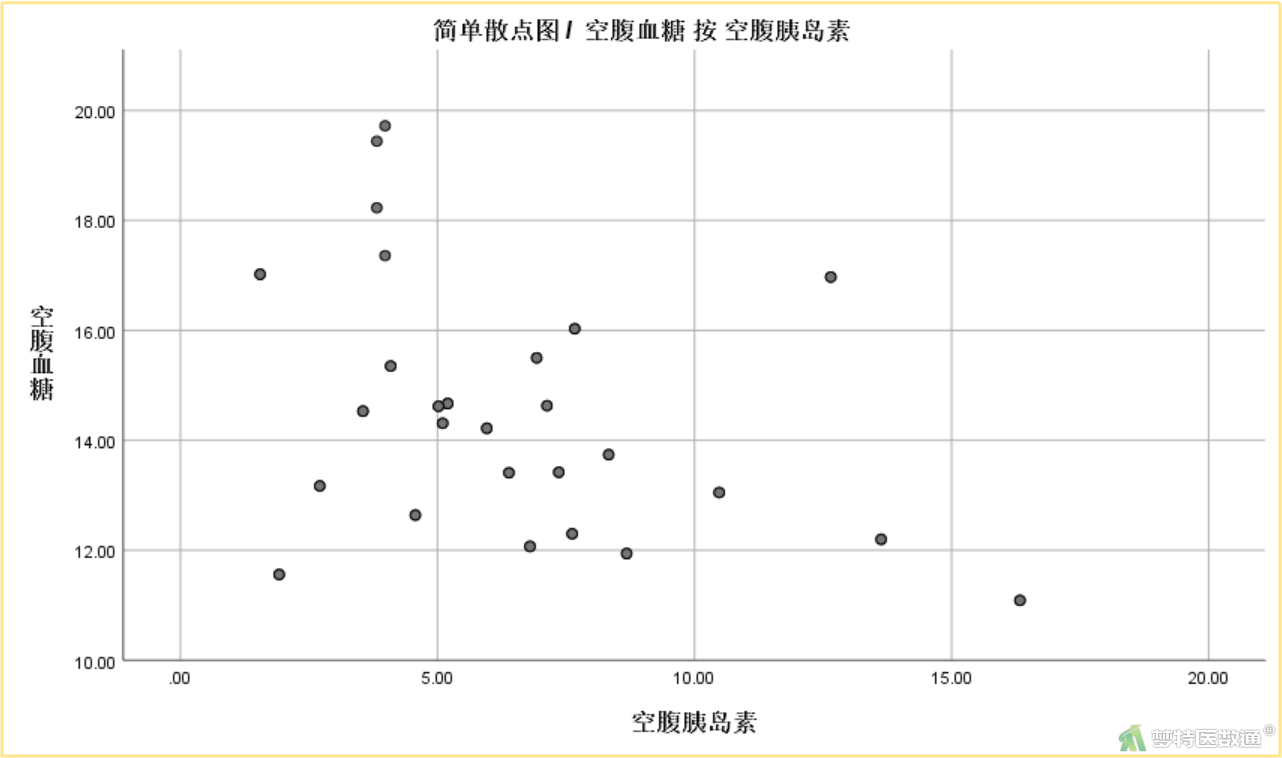
③ 参照步骤②绘制自变量“空腹胰岛素”与因变量“空腹血糖”的散点图如图5所示。

(2) 结果解读

由图4可知，“糖化血清蛋白”与“空腹血糖”之间存在线性关系。由图5可知，“空腹胰岛素”与“空腹血糖”之间存在线性关系。每个自变量和因变量的线性关系只是针对自变量为连续变量而言的，因此本例中分类型自变量与因变量之间的线性关系可以忽略。综上，本案例满足条件2。

2. 设置哑变量

根据数据类型判断，“经济水平”为无序多分类资料，需要将“经济水平”转化为哑变量后，进行多重线性回归。以下将对“经济水平”进行哑变量设置。

(1) 软件操作

① 点击“转换”—“创建虚变量”(图6)。

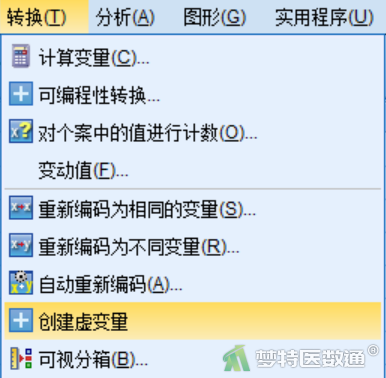
② 在“创建虚变量”对话框中将变量“经济水平”选入右侧“针对下列变量创建虚变量”框中，然后在“创建主效应虚变量”下的“根名称-每个选定变量各一个”中输入虚拟变量的名称“Income”；点击“确定”，完成虚拟变量设置(图7)。

(2) 结果解读

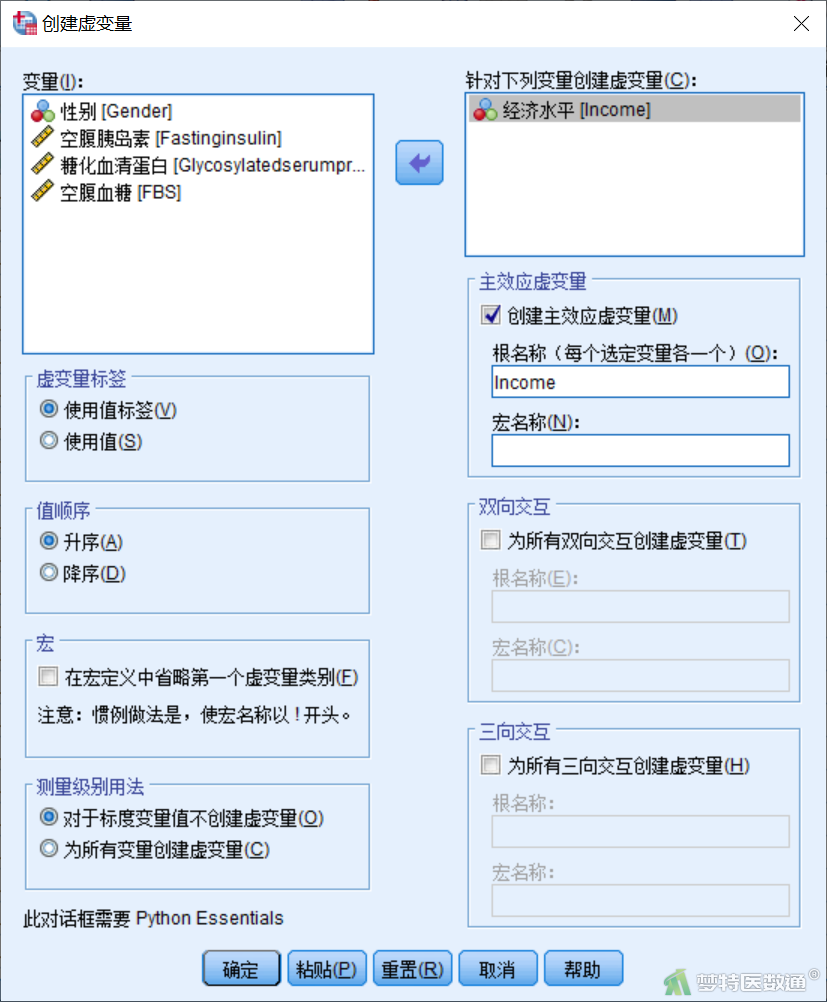
上述步骤运行结束后可以在数据编辑页面看到新生成的3个哑变量(图8)，随后就可以进行多重线性回归。

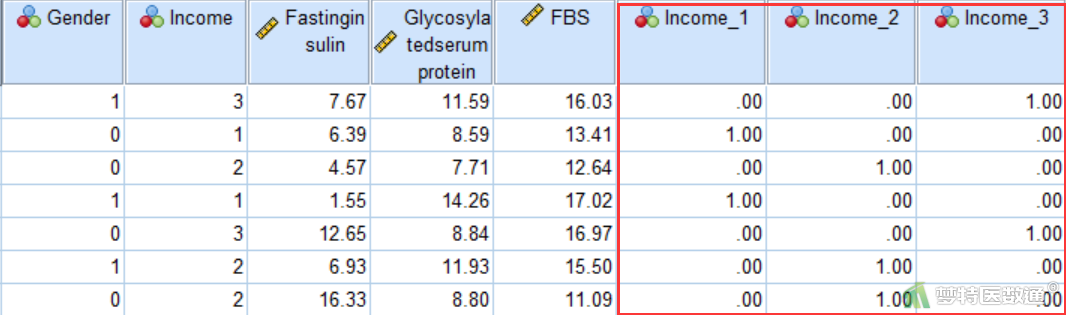
3.条件3~7判断

在线性回归过程中判断是否符合条件3~7。

(1) 软件操作

① 选择“分析”—“回归”—“线性” (图9)。

② 在弹出的对话框中，将因变量“空腹血糖”选入右侧“因变量”框、将自变量“性别”、“空腹胰岛素”、“糖化血清蛋白”选入右侧“自变量”框(图10)。

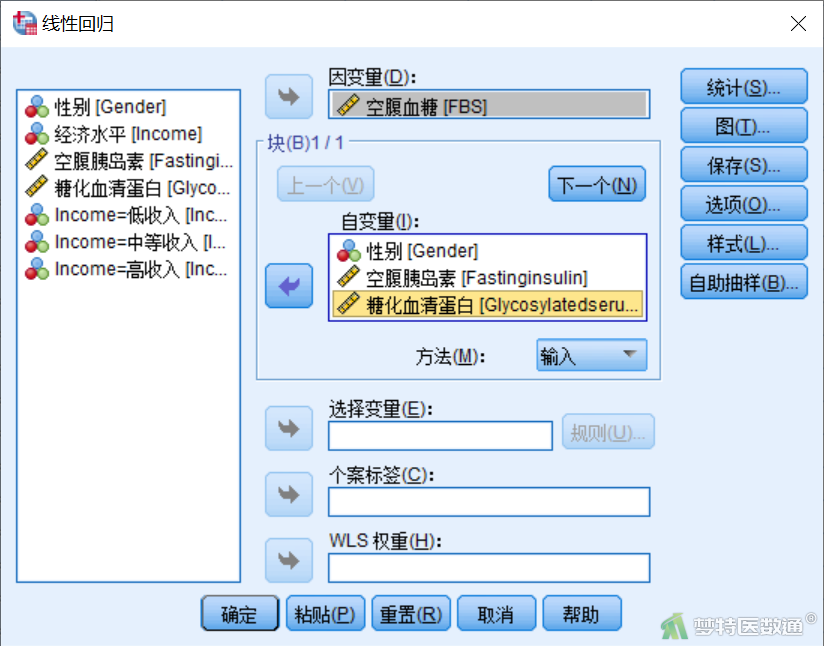
③ 然后点击“下一个”。将“中等收入”和“高收入”两个虚拟变量同时选入右侧“自变量”，此时表示以“低收入”为参照水平；“方法”选择“输入”，即哑变量设置的同进同出原则(图11)。

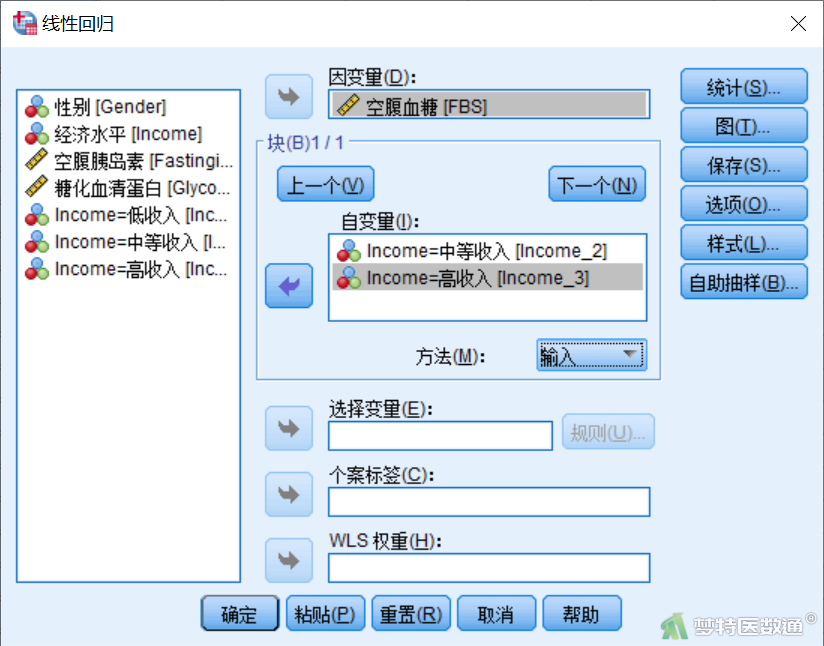
④ 点击右侧“统计”，选择“回归系数中的“估算值”、“置信区间”选项，选择“残差中的“德宾-沃森”、“个案诊断”选项，选择“模型拟合”、“描述”、“部分相关性和偏相关性”、“共线性诊断”选项，点击“继续” (图12)。

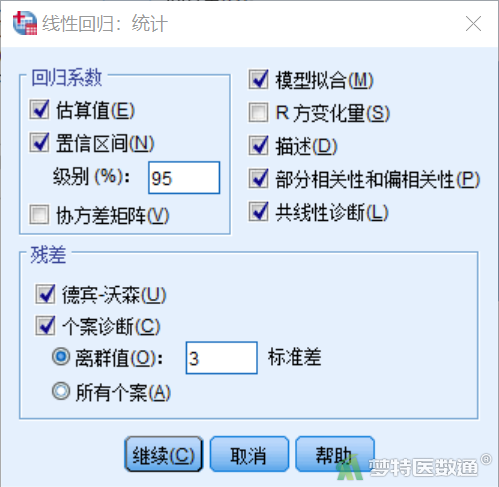
⑤ 点击右侧“图”，分别在“Y:”和“X:”框内添加“*ZRESID(标准化残差)”和“*ZPRED(标准化预测值)”。在“标准化残差图”中勾选“直方图”和“正态概率图”。勾选“生成所有局部图”，点击“继续”(图13)。

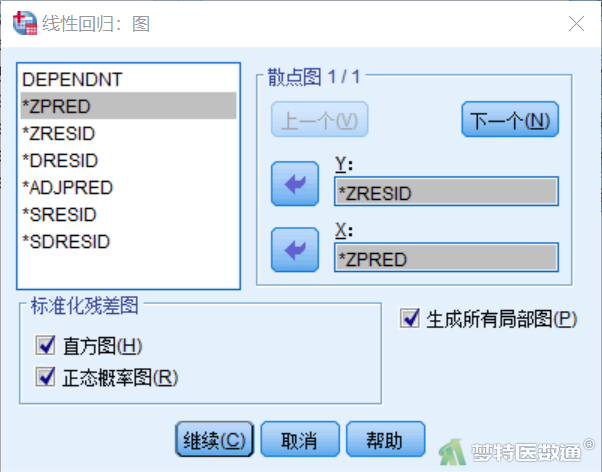
⑥ 点击右侧“保存”，在弹出的对话框中，选择“预测值 ”中的“未标准化 ”选项，选择“残差”中的“学生化 ”、“学生化删除后”选项， 在“距离”中勾选“库克距离”和“杠杆值”，点击“继续” (图14)。回到“线性回归”对话框，点击“确定”。

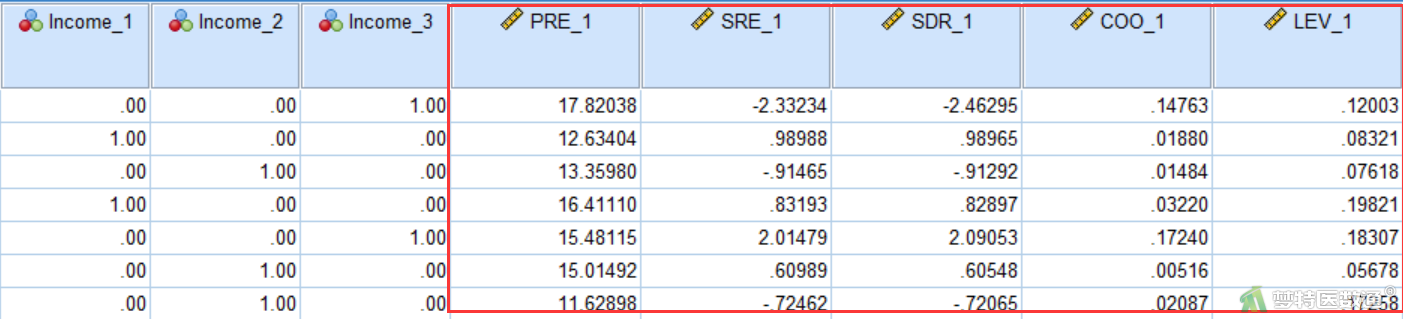
如图15所示，经过上述操作后，“变量视图” 和“数据视图”对话框中会增加5个变量，这5个变量分别是“未标化预测值(PRE_1)”、“学生化残差(SRE_1)”、“学生化删除残差SDR_1)”、“Cook距离(COO_1)”以及“杠杆值(LEV_1)” 。

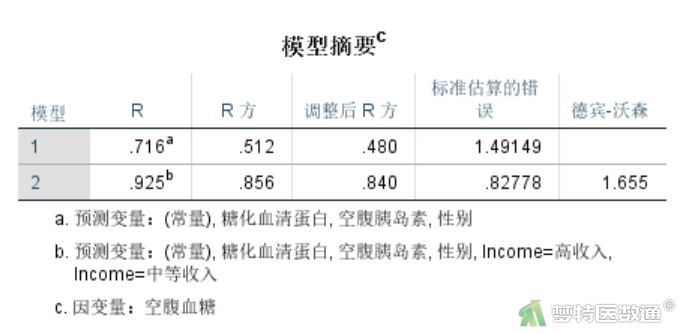
(2) 独立性判断

图16是模型摘要，其中的“Durbin-Watson (德宾-沃森/D-W)”检验通常用来检测残差是否存在自相关，Durbin-Watson检验值分布在0~4之间，越接近2，观测值相互独立的可能性越大。需要注意的是，判断观测值是否独立，主要取决于研究设计和数据收集阶段的质量控制，Durbin-Watson检验最好用于辅助判断。本例D-W值为1.655，可以认为观测值相互独立，满足条件3。

(3) 多重共线性判断

可通过“相关系数”和“容差”、“方差膨胀因子”来判断自变量之间有无多重共线性。

图17是相关系数表，即自变量之间的相关系数矩阵。自变量之间的相关系数如果大于0.7，则提示可能存在多重共线性。如图所示，本例任意两个自变量的相关系数都小于0.7，提示不存在多重共线性。

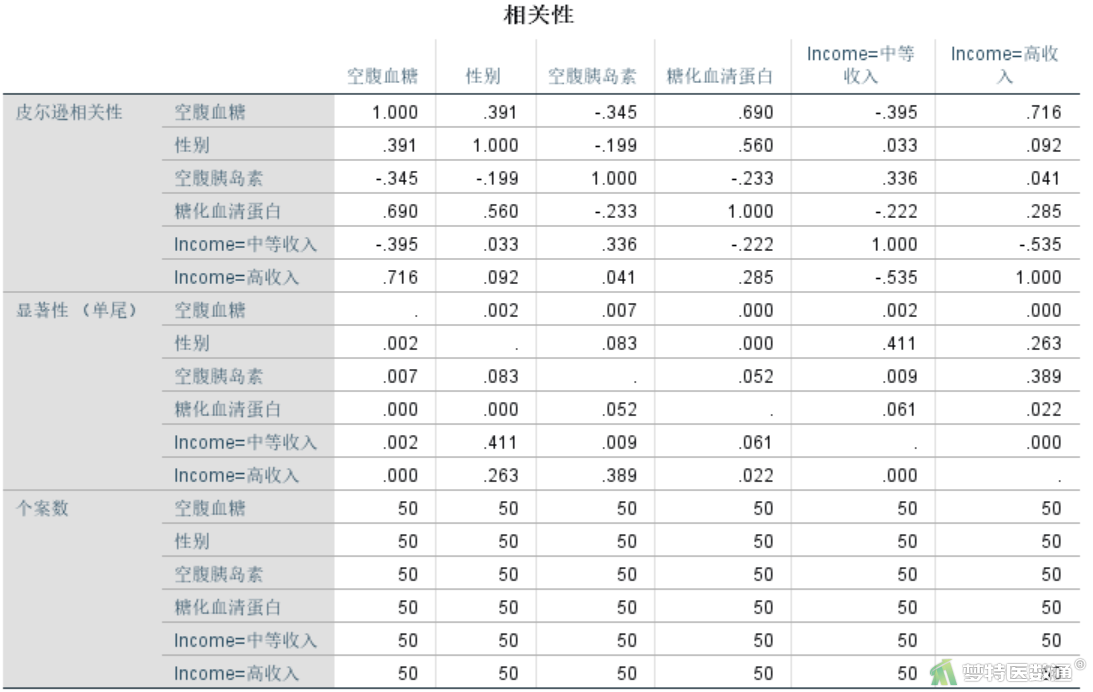
图18是模型系数，显示本例的容差和方差膨胀因子。如果“Tolerance(容差)”小于0.1或“VIF(方差膨胀因子)”大于10，则提示有严重共线性存在。本例中，各变量的容差均远大于0.1，方差膨胀因子均远小于10，提示自变量之间不存在严重多重共线性。如果数据存在严重多重共线性，需用复杂的方法进行处理，其中最简单的是剔除引起共线性的因素之一，剔除哪一个因素可以基于理论依据。

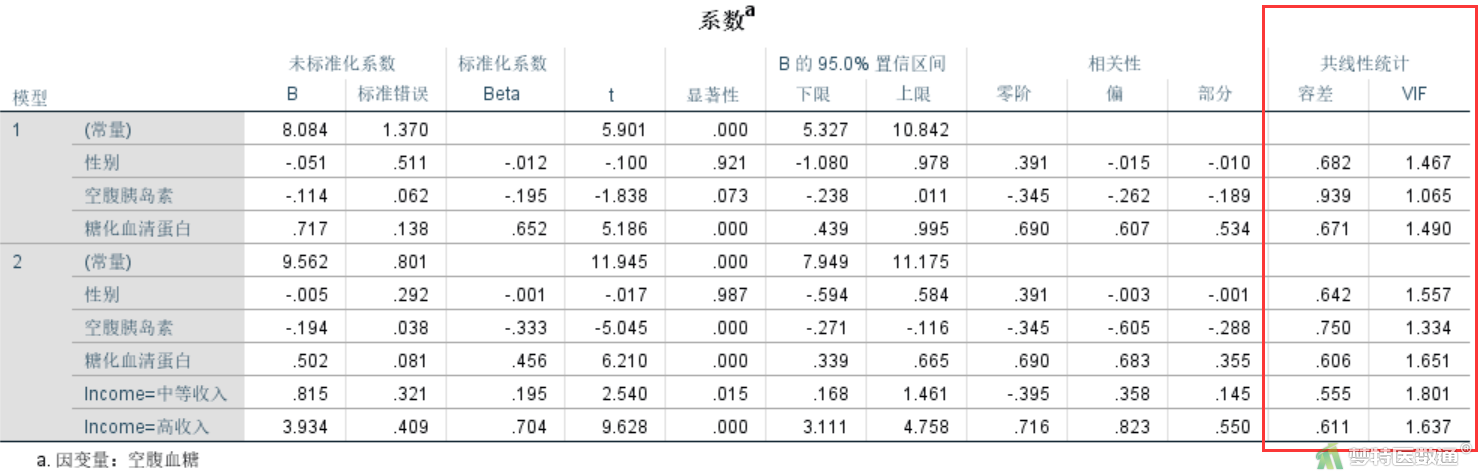
综上，本案例满足条件5。

(4) 异常值判断

本例可通过“个案诊断”选项来判断是否存在异常值点，结果没有出现个案诊断的异常值列表，提示本例没有异常值。也可通过“库克距离”用来判断强影响点是否为因变量的异常值点。一般认为当D<0.5时不是异常值点，当D>0.5时是异常值点。由图19可知，最大库克距离D为0.234<0.5，提示不存在显著异常值。

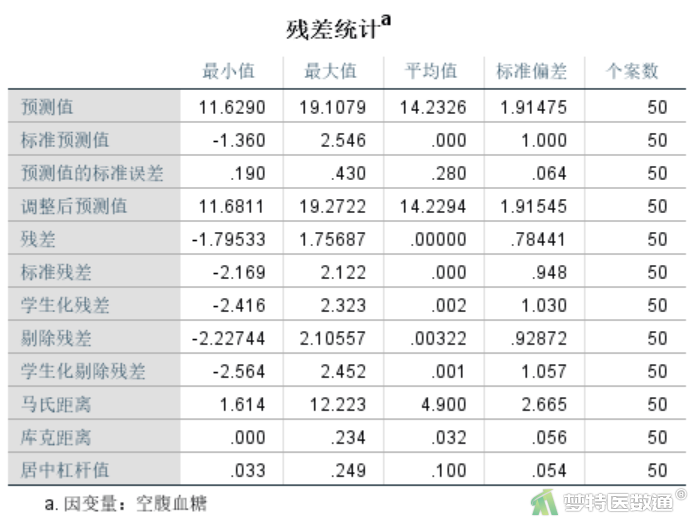
综上，本案例满足条件4。

(5) 正态性判断

可通过标准化残差直方图和残差P-P图来判断残差的正态性。图20是回归模型标准化残差的直方图，可见标准化残差近似服从正态分布。

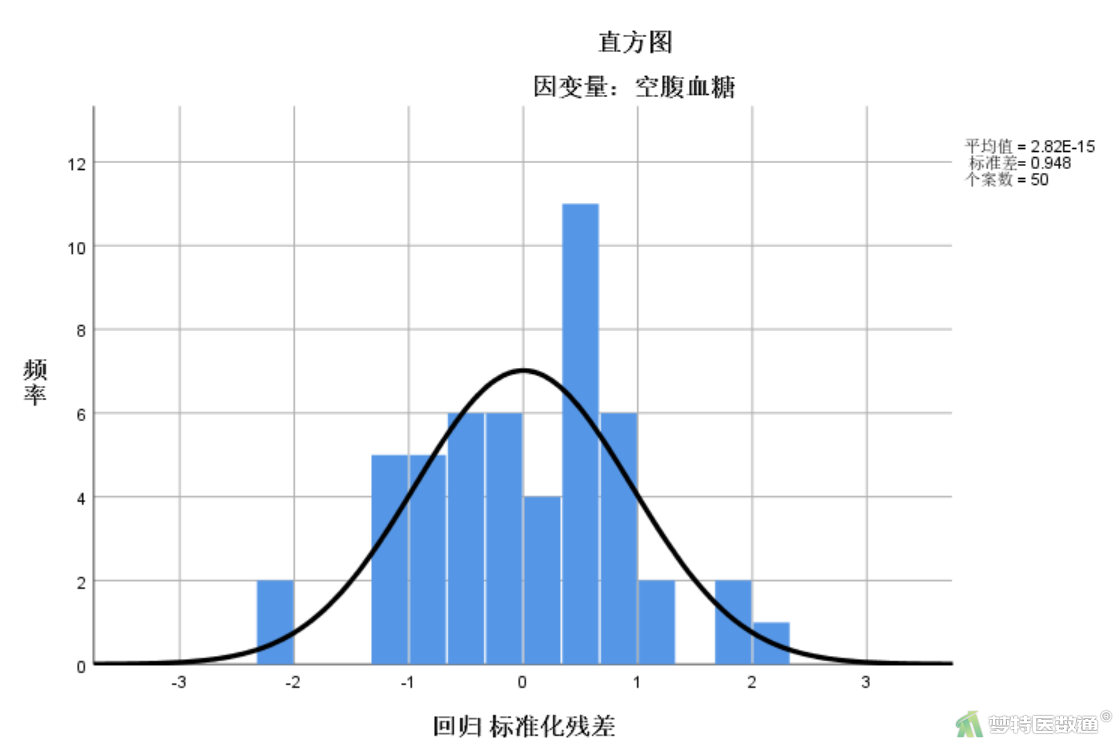
图21是回归标准化残差的正态P-P图，可见P-P图各点沿对角线分布，提示回归残差近似服从正态分布。

综上，本案例满足条件6。

(6) 方差齐性判断

可通过回归模型的标准化残差与标准化预测值的散点图来判断方差齐性。由图22可见，预测值和对应的残差分布较为均匀，数据点均分布在±3个标准差之内，并未出现特殊的分布形式(如漏斗或者扇形)，提示残差的方差齐，满足条件7。

(二) 变量筛选

从图18列出的模型系数可知，自变量“性别”的t=-0.017，P=0.987，无统计学意义，应该被移除模型。

① 选择“分析”—“回归”—“线性”(图9)。

② 在弹出的对话框中，将变量“性别”从右侧“自变量”框中移除后，进行操作(图23)。

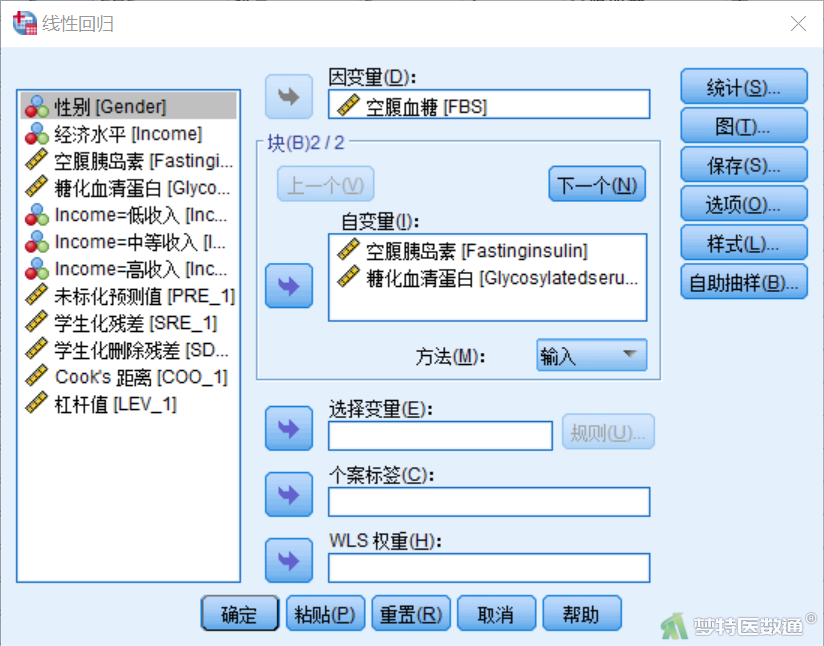
③ 其余步骤同前，可直接点击“确定”，输出结果。

(三) 统计描述及判断

1. 软件操作

经过上述操作，已经输出了多重线性回归模型的结果。

2. 结果解读

(1) 模型拟合程度

图24列出模型的拟合程度。R为复相关系数，为0.925；R²为决定系数，用来反映模型预测的准确性，本例决定系数R²=0.856，提示自变量可以解释85.6%的因变量变异，即成年人的体重能解释双肾总体积的85.6%的变异。但是R²会受自变量个数的影响，夸大自变量对因变量变异的解释程度，自变量越多，R²越大。为校正自变量个数的影响，一般采用后面的调整后R²，调整自变量个数对结果的影响。本例的调整R²=0.844，提示自变量可以解释84.4%的因变量变异。

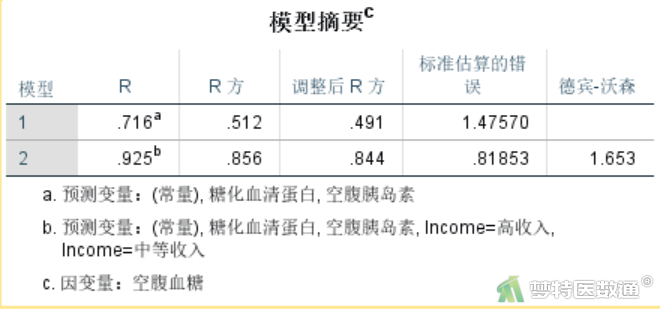
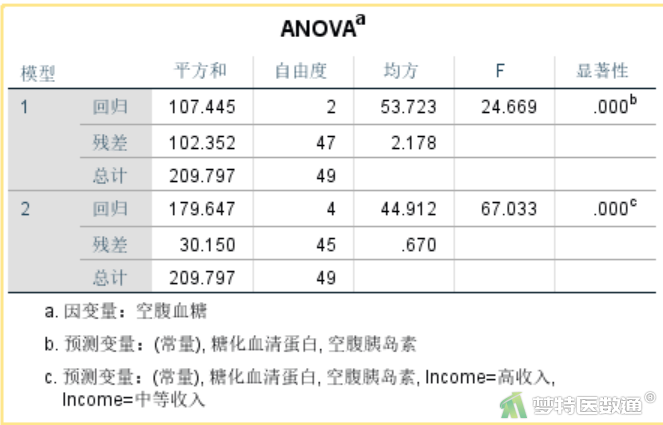
图25为模型统计检验结果，采用的是方差分析，结果显示F=67.033，P<0.001，提示模型有统计学意义。如果P>0.05，则说明回归模型没有统计学意义。

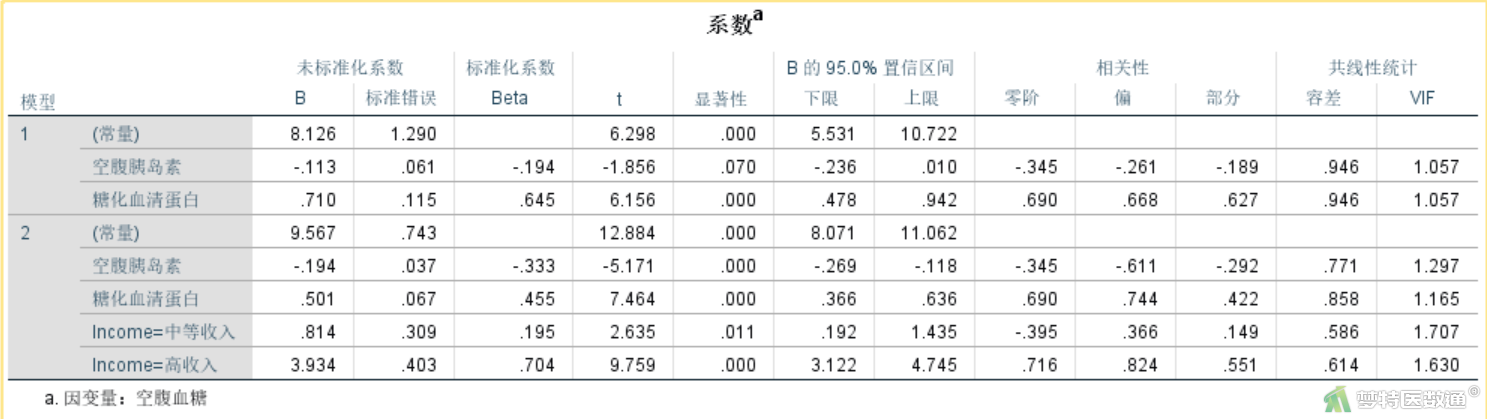
(2) 回归系数解释

图26为回归方程的系数。列出了截距和自变量的回归系数及回归系数95%CI、统计量t值及P值。可知，回归模型的截距为9.567，表示自变量取值为0时，因变量的取值，并无实际专业意义。变量“空腹胰岛素”的非标准化系数(即斜率)为-0.194 (95%CI：-0.269~-0.118，P<0.001)，表示“空腹胰岛素”每增加1mmol/L，空腹血糖减少0.194 mmol/L；变量“糖化血清蛋白”的非标准化系数(即斜率)为0.501 (95%CI：0.366~0.636，P<0.001)，表示“糖化血清蛋白”每增加1%，空腹血糖增加0.501 mmol/L。相比“低收入”人群而言，“中等收入”人群的非标准化系数为0.814 (95%CI：0.192~1.435，P=0.011)，表示“中等收入”人群比“低收入”人群空腹血糖高0.814 mmol/L；相比“低收入”人群而言，“高收入”人群的非标准化系数为3.934 (95%CI：3.122~4.745，P<0.001)，表示“高收入”人群比“低收入”人群空腹血糖高3.934 mmol/L。

据此可以写出本案例的回归方程为：

空腹血糖 = 9.567 - 0.194×空腹胰岛素 + 0.501×糖化血清蛋白+ 0.814×(经济水平=中等收入) + 3.934×(经济水平=高收入)

根据此方程输入相关自变量数值即可对空腹血糖进行预测。

四、结论

本研究采用多重线性回归模型考察“空腹血糖”是否受到性别、经济水平、空腹胰岛素和糖化血清蛋白的影响。通过绘制散点图，提示空腹胰岛素和糖化血清蛋白与空腹血糖之间存在线性关系，通过专业判断和Durbin-Watson检验提示数据之间相互独立，通过库克距离分析，提示数据不存在需要删除的异常值；通过相关系数、方差膨胀因子和容忍度判断自变量之间不存在严重多重共线性，通过绘制标准化残差直方图和残差P-P图，提示残差服从正态分布；通过绘制残差图，提示残差方差齐。满足多重线性回归分析条件。

多重线性回归分析结果解读为，在其他变量不变的情况下，“空腹胰岛素”每增加1 mmol/L，空腹血糖减少0.194 mmol/L (β=-0.194，95%CI：-0.269~-0.118；P<0.001)；“糖化血清蛋白”每增加1%，空腹血糖增加0.501 mmol/L (β=0.501，95%CI：0.366~0.636；P<0.001)；“中等收入”人群比“低收入”人群空腹血糖高0.814 mmol/L (β=0.814，95%CI：0.192~1.435；P=0.011)；“高收入”人群比“低收入”人群空腹血糖高3.934 mmol/L(β=3.934，95%CI：3.122~4.745，P<0.001)。

线性回归分析方程为：空腹血糖 = 9.567 - 0.194×空腹胰岛素 + 0.501×糖化血清蛋白+ 0.814×(经济水平=中等收入) + 3.934×(经济水平=高收入)。回归模型具有统计学意义，F=67.033，P<0.001；模型可以解释84.4%的因变量的变异(adjusted R²=0.844)。

五、分析小技巧

(一) 各观测值之间的独立性检测

• 判断观测值是否独立，主要取决于研究设计和数据收集阶段的质量控制，Durbin-Watson检验最好用于辅助判断。Durbin-Watson检验值分布在0~4之间，越接近2，观测值相互独立的可能性越大。且根据Pr <DW和Pr >DW，可得知正相关检验和负相关检验的P值大小，更容易客观的判断独立性。

(二) 异常值检测

• 库克距离用来判断强影响点是否为因变量的异常值点。一般认为当D<0.5时不是异常值点，当D>0.5时认为是异常值点。
• 并非所有的异常点都意味着结果不好，有时候发现异常点可能会提示有更重要的信息。如果出现异常点，首先应检查数据是否录入错误，也可以选择其他相应模型来拟合，或者需要收集更多的数据来证实。

(三) 残差的正态性检测

• 如果残差不符合正态分布，可以考虑对因变量进行数据变换，使其服从正态分布后再拟合线形回归模型。

(四) 残差的方差齐性检测

• 残差的方差齐是指在自变量取值范围内，对于任意自变量取值，因变量都有相同的方差。线形回归中，残差的方差齐实际上要比残差正态分布重要。如果这一条件不满足，可对因变量进行变量变换，使其满足残差方差齐，也可以采用加权回归分析，消除方差的影响。

(五) 变量筛选

• 多重回归分析中，变量的筛选一般有向前筛选(selection=forward)、向后筛选(selection=backward)、逐步筛选(stepwise)三种基本策略。
• 向前筛选是变量不断进入回归方程的过程。首先，选择与因变量具有最高线性相关系数的变量进入方程，并进行回归方程检验；其次，在剩余的变量中寻找与因变量偏相关系数最高的变量进入回归方程，并对新建立的回归方程进行检验；一直重复这个过程，直到再也没有可进入方程的变量为止。
• 向后筛选是变量不断剔除出回归方程的过程。首先，所有变量全部引入回归方程，并对回归方程进行检验，然后在回归系数不显著的变量中，剔除t检验值最小的变量，并对模型进行检验；直到回归方程中所有变量的回归系数均显著，则回归模型确定。
• 逐步筛选在向前筛选的基础之上，结合向后筛选策略，在每个变量进入方程后再次判断是否存在可以剔除方程的变量。因此，逐步筛选在引入变量的每一个阶段都提供了剔除不显著变量的机会。

(六) 回归模型

• 在进行回归分析时，要注意避免对数据的过渡挖掘，不能将回归模型分析的结果随意延伸到自变量取值范围以外的数值。也不能随意将模型分析结果延伸到因果关系。

(七) 模型评价

常见的回归模型评价指标有：决定系数R²、校正决定系数adjusted R²和均方根误差RMSE等。实际分析时，可以综合多个指标，并结合模型所反映的实际情况来判断。

• 决定系数R² (determination coefficient)反映了因变量的变异能够被自变量解释的比例，或者说方程中的自变量解释了因变量变异的多少。R²越大，表示方程中自变量解释能力越强。但该指标有一缺陷，即其值随着自变量的增多而增加，即使加入无意义的变量，该指标值也会随之增加，因此不能较好地反映模型优劣。
• 校正决定系数adjusted R²(adjusted determination coefficient) 是对决定系数的修正。当有统计学意义的变量进入方程时，该指标随之增大，而当无统计学意义的变量进入方程时，其值减小。值越大表明模型越好，是衡量模型优劣的重要指标之一。
• 均方根误差RMSE主要反映模型的估计精度，值越小越好。一般会随模型中自变量个数增加而减小，这一性质与校正系数相似。