在前面文章中介绍了“两因素方差分析 (Two-way ANOVA)一(无交互作用)——jamovi软件实现”,本篇文章将实例演示在jamovi软件中实现两因素方差分析——有交互作用时的操作步骤。
关键词:jamovi; 两因素方差分析; 交互作用; 主效应; 单独效应; 简单效应
一、案例介绍
观察A、B两种镇痛药物联合运用在产妇分娩时的镇痛效果。A药(Drug_A)取3个剂量:1.0、2.5、5.0 mg;B药(Drug_B)取3个剂量:5.0、15.0、30.0 μg,共9个处理组。将27名产妇随机分成9组,每组3名产妇,记录每名产妇分娩时的镇痛时间 (min)。试分析A、B两药联合运用的镇痛效果。部分数据见图1,本案例数据可从“附件下载”处下载。
二、问题分析
本案例的分析目的是分析A、B两种药物联合运用的镇痛效果。临床上,药物之间联合运用往往会相互影响,这种影响可能为正向的增强作用,也可能为反向的拮抗作用。针对这种情况,可以使用多因素方差分析,由于本案例为药物A和药物B两个因素,因此可以使用两因素方差分析。但需要满足6个条件:
条件1:观察变量唯一,且为连续变量。本研究中观察变量只有镇痛时间,且为连续变量,该条件满足。
条件2:有2个因素,且都为分类变量。本研究中有A药物、B物2个因素,均为分类变量,该条件满足。
条件3:观测值之间相互独立。本研究中各研究对象的观测值都是独立的,不存在互相干扰的情况,该条件满足。
条件4:观察变量不存在显著的异常值,该条件需要通过软件分析后判断。
条件5:各组、各水平观测值为正态(或近似正态)分布,该条件需要通过软件分析后判断。
条件6:相互比较的各处理水平(组别)的总体方差相等,即方差齐同,该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 适用条件判断
由于本案例组别较多且每组观察数很少,所以使用残差检查异常值、正态性及方差齐性。
1. 生成因变量残差
(1) 软件操作
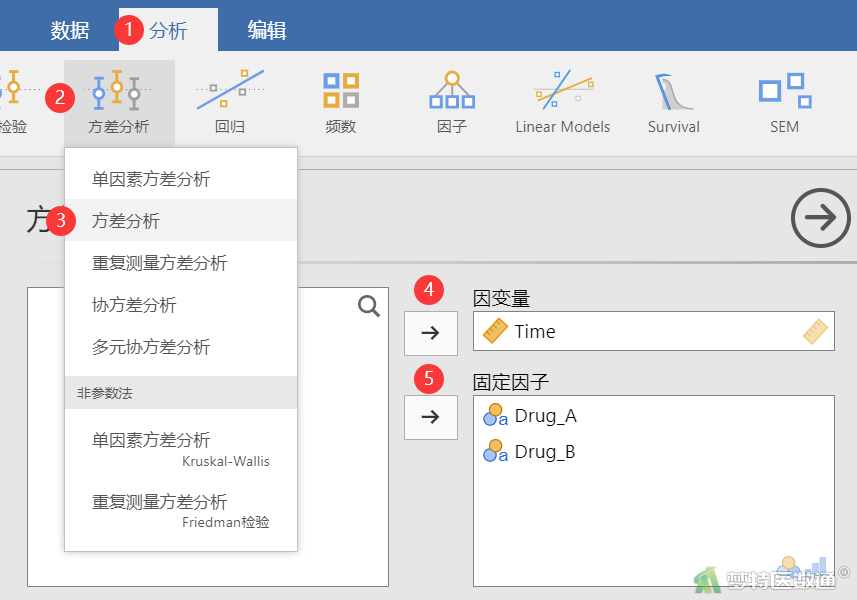
选择“分析”—“方差分析”—“方差分析”,将变量“Time”选入右侧“因变量”框,将“Drug_A”、“Drug_B”选入右侧“固定因子”框(图2)。
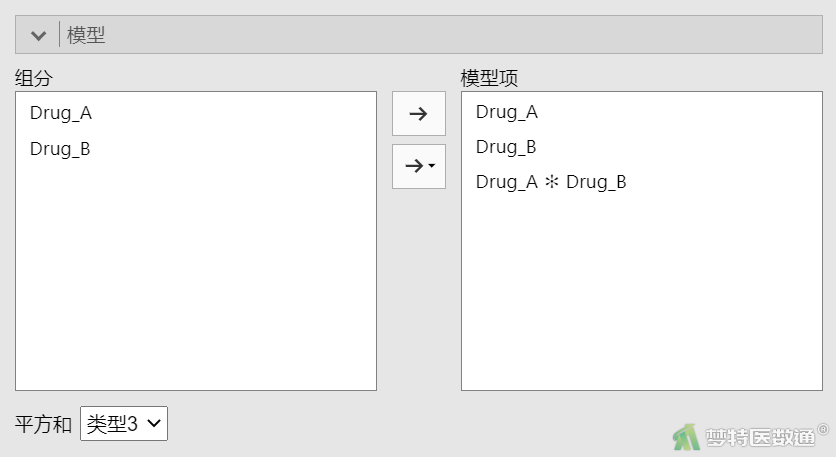
②将“Drug_A”、“Drug_B”选入右侧“模型项”框,再将“Drug_A”、“Drug_B”同时选中,将其交互项“Drug_A*Drug_B”选入右侧“模型项”框(图3);在“保存”中勾选“残差”(图4)。

(2) 结果解读
在“数据”视图中生成了一列新的变量“残差”(图5)。
2. 条件4判断(异常值判断)
(1) 软件操作
①选择“分析”—“探索”—“描述”,将“残差”选入右侧“变量”框,将“Drug_A”、“Drug_B”选入右侧“拆分”框(图6)。
②在“绘图”下的“箱线图”中勾选“箱线图”—“标注离群值”和“数据”—“散点”(图7),结果如图8所示。
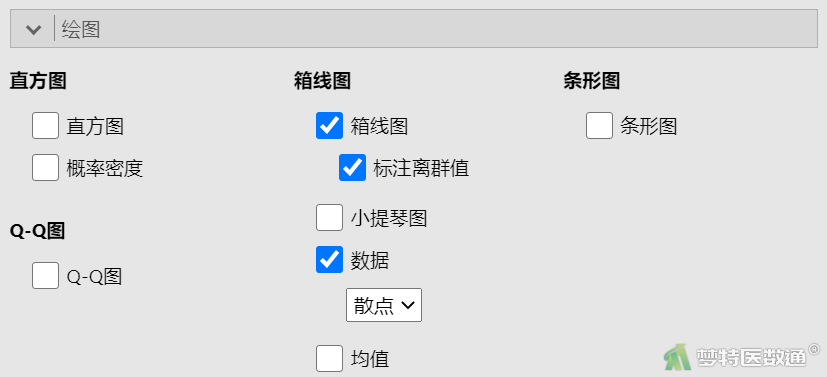
(2) 结果解读
残差的箱线图未提示任何异常值和极端值(图8),满足条件4。
3. 条件5判断(正态性检验)
(1) 软件操作
两因素方差分析时,可分别考察每一组的正态性或使用残差考察整体数据的正态性。选择“分析”—“探索”—“描述”,在“统计”中勾选“正态性”—“Shapiro-Wilk检验”(图9),结果如图10所示。

(2) 结果解读
正态性检验结果(图10)显示各组的P值分别为0.726、0.537、1.000、0.220、0.220、1.000、0.220、0.702、0.637,均>0.1,提示各组数据均服从正态分布。本案例满足条件5。若考察残差的正态性,则在方差分析分析模块中,在“适用条件判断”中勾选“正态性检验”和“Q-Q图”。
4. 条件6判断(方差齐性检验)
(1) 软件操作
在“方差分析”模块中,在图2和图3步骤上,在“适用条件判断”中勾选“方差齐性检验”(图11),结果如图12所示。
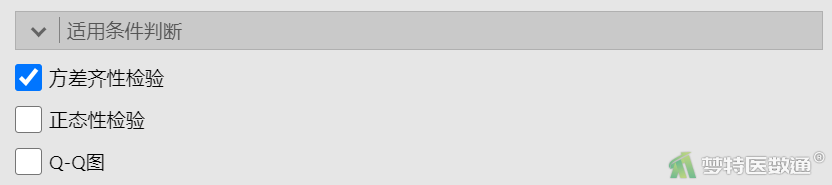
(2) 结果解读
图12“Homogeneity of Variances Test (方差齐性检验)”显示,两种检验方法的P值均>0.1;提示数据总体方差相等。本案例满足条件6。
(二) 统计描述
1. 软件操作
①选择“分析”—“探索”—“描述”,将观察变量“Time”选入右侧“变量”框,将“Drug_A”和“Drug_B”选入右侧“拆分”框(图13)。
②在“统计”下的“样本量”中勾选“个案数”,在“集中趋势”中勾选“均值”,在“离散趋势”中勾选“标准差”、“最小值”和“最大值”(图14),结果如图15所示。
2. 结果解读
由各组的均值和标准差结果(图15)可知,药物A在1.0 mg水平,药物B为5.0、15.0、30.0 μg水平时,镇痛时间分别为:83.333±20.207、100.000±18.028、85.000±10.000 min;药物A在2.5 mg水平,药物B为5、15、30 μg水平时,镇痛时间分别为:90.000±21.794、115.000±21.794、135.000±15.000 min;药物A在5.0 mg水平,药物B为5、15、30 μg水平时,镇痛时间分别为:110.000±21.794、95.000±27.839、176.667±15.275 min。
(三) 两因素方差分析
1. 软件操作
在“方差分析”模块中,在图2和图3步骤上,在“边际估计均值”框中,将“Drug_A”和“Drug_B”先后依次选入右侧“边际均值”框,在“输出”下勾选“边际均值图”和“边际均值表”(图16),结果如图17和图18所示。
2. 结果解读
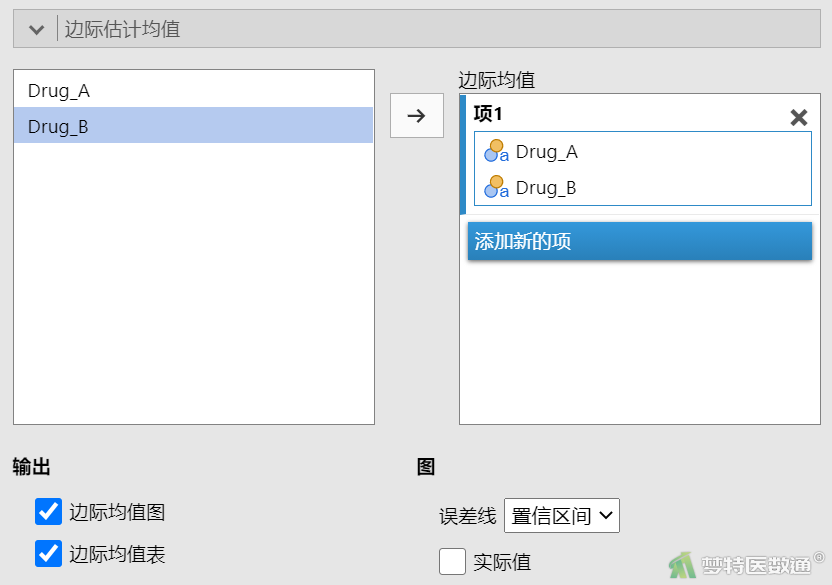
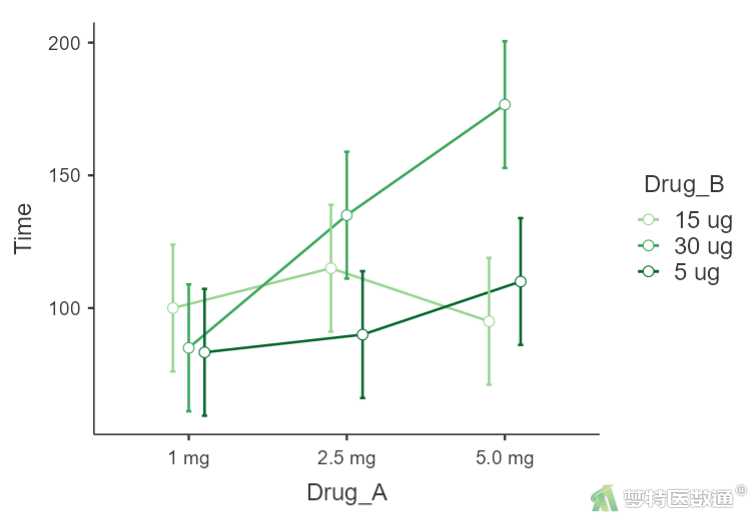
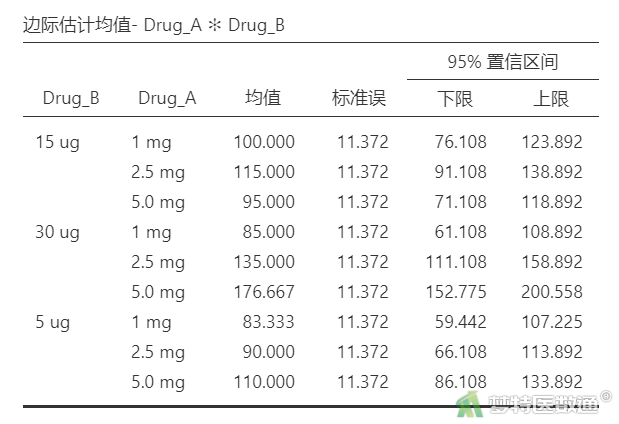
估算边际均值图(图17)绘制了各组镇痛时间的变化情况,可见两药物的变化曲线趋势并不平行,存在明显的交互作用。边际估计均值-Drug_A*Drug_B(图18)表格中提供了各组的“估算边际均值(偏最小二乘均值)”、“标准误”及均值的“95%置信区间”。
(四) 交互作用判断
由于本案例有两个因素(药物A和药物B),因此需要首先判断两个因素(两种药物)之间是否存在交互作用。尽管通过图17的变化趋势已经提示两药物之间可能存在交互作用,但仍需要统计学推断结果的支持。如果交互作用有统计学意义,则需要分析简单效应。
1. 软件操作
在“模型拟合”下勾选“整体模型检验”,在“效应量”中勾选“Ƞ²值”、“偏Ƞ²”、“ω²”(图19),结果如图20所示。
2. 结果解读
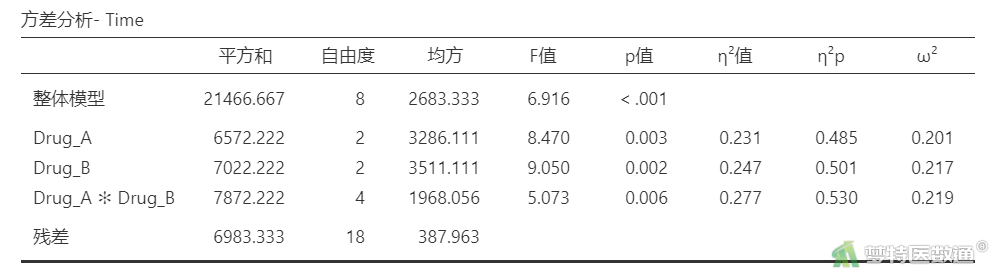
“方差分析-Time”(图20)显示,Drug_A与Drug_B之间的交互作用结果为FDrug_A*Drug_B=5.073,P=0.006,提示Drug_A与Drug_B之间的交互作用有统计学意义。η²p效应量为0.530,为大效应。因此,本案例需要分析简单效应。
(五) 简单效应分析
1. 软件操作
①选择“分析”—“R”—“Rj Editor + (R语言jamovi编辑器+)”(图21)。
②在Rj Editor中,有两个版本的R语言可供选择,即jamovi自带的版本(jamovi R)和已经安装的R语言(System R),此处选择后者(图22)。
③在R软件中安装“bruceR”包、“magrittr”包和“jmvconnect”包;
④将Drug_A、Drug_B和Time选入变量(图23),并输入程序代码后点击右边绿色三角形按钮运行程序,结果如图24—图29所示。
2. 结果解读
(1) 药物A的简单效应
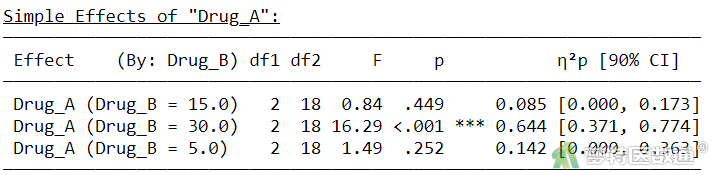
由“Simple Effects of ‘Drug_A’ (药物A的简单效应)”结果(图24)可知,在药物B为5.0 μg水平时,药物A各水平之间的镇痛时间差异无统计学意义(F=1.49,P=0.252);在药物B为15.0 μg水平时,药物A各水平之间的镇痛时间差异无统计学意义(F=0.84,P=0.449);但在药物B为30.0 μg水平时,药物A各水平之间的镇痛时间差异有统计学意义(F=16.29,P<0.001)。
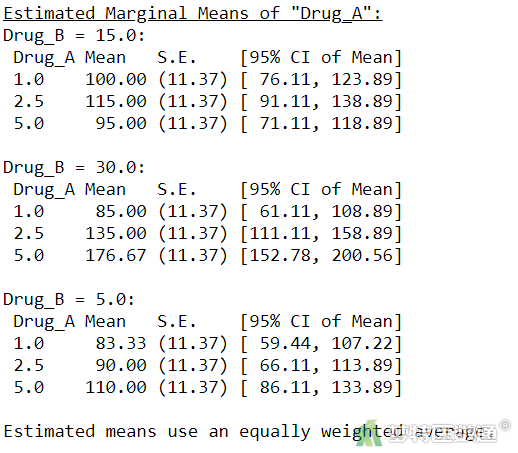
各组“Mean (估算边际均值(偏最小二乘均值))”、“SE (标准误)”及均值的“95% Confidence Interval (95%CI)”(图25)与边际估计均值-Drug_A*Drug_B(图18)的结果一致。
(2) 药物B的简单效应
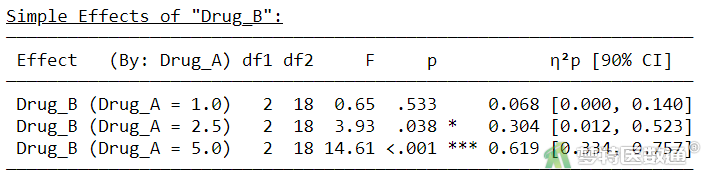
由“Simple Effects of ‘Drug_B’ (药物B的简单效应)” (图26)可知,在药物A为1.0 mg水平时,药物B各水平之间的镇痛时间差异无统计学意义(F=0.65,P=0.533);在药物A为2.5 mg水平时,药物B各水平之间的镇痛时间差异有统计学意义(F=3.93,P=0.038);但在药物A为5.0 mg水平时,药物B各水平之间的镇痛时间差异有统计学意义(F=14.61,P<0.001)。
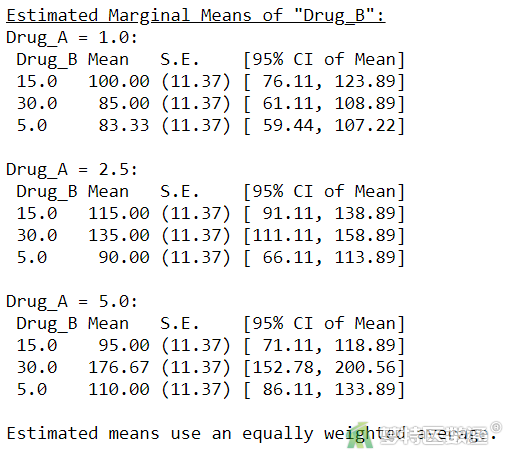
各组“Mean (估算边际均值(偏最小二乘均值))”、“SE (标准误)”及均值的“95% Confidence Interval (95%CI)”(图27)与边际估计均值-Drug_A*Drug_B(图18)的结果一致。
(六) 事后检验(两两比较)
1. 药物A的简单效应事后检验
上面分析得出了“在药物B为30.0 μg水平时,药物A各水平之间的镇痛时间差异有统计学意义”的结论。由于药物A在药物B为5.0 μg和15.0 μg水平下的整体检验差异无统计学意义,此时便不再进行事后两两比较。现对药物A在药物B为30.0 μg水平时进行事后检验,结果如图28所示。
“Pairwise Comparisons of ‘Drug_A’ (事后检验比较‘Drug_A’)”结果(图28)中提供了药物B在不同水平时药物A不同浓度间通过“Bonferroni (邦弗罗尼)”法两两比较的“均数差”、“SE (标准误)”、“df (自由度)”、“t (统计量t值)”、“P* (校正P值)”。
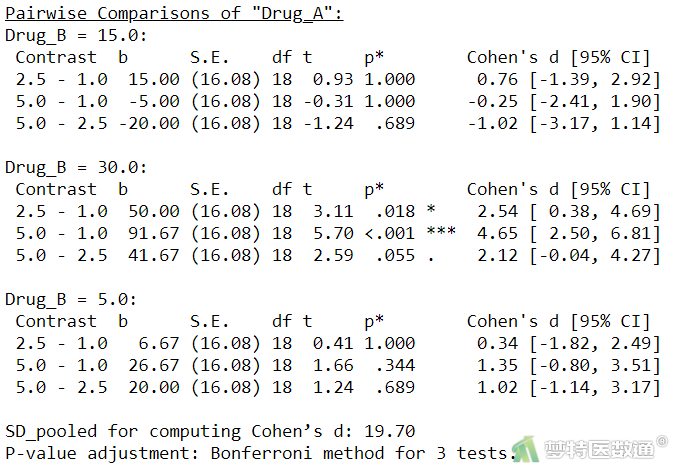
可知,在药物B为30.0 μg水平时,药物A浓度为2.5 mg和5.0 mg与1.0 mg相比,均值差逐渐增大。2.5 mg比1.0 mg时均值增加了50.00 min,至5.0 mg时增加了91.67 min,差异均有统计学意义(P<0.001);2.5 mg到5.0 mg时增加了41.67 min,差异无统计学意义(P=0.055)。表明,在药物B为30.0 μg水平时,随着药物A浓度的增加,镇痛时间呈上升趋势。
2. 药物B的简单效应事后检验
上面分析得出了“在药物A为2.5 mg和5.0 mg水平时,药物B各水平之间的镇痛时间差异均有统计学意义”的结论。由于药物B在药物A为1.0 mg水平下的整体检验差异无统计学意义,此时便不再进行事后两两比较。现对药物B在药物A为2.5 mg和5.0 mg水平时进行事后检验,结果如图29所示。
“Pairwise Comparisons of ‘Drug_B’ (事后检验比较‘Drug_B’)”结果(图29)中提供了在药物A在不同水平时,药物B不同浓度间通过“Bonferroni (邦弗罗尼)”法两两比较的“均数差”、“SE (标准误)”、“df (自由度)”、“t (统计量t值)”、“P* (校正P值)”。
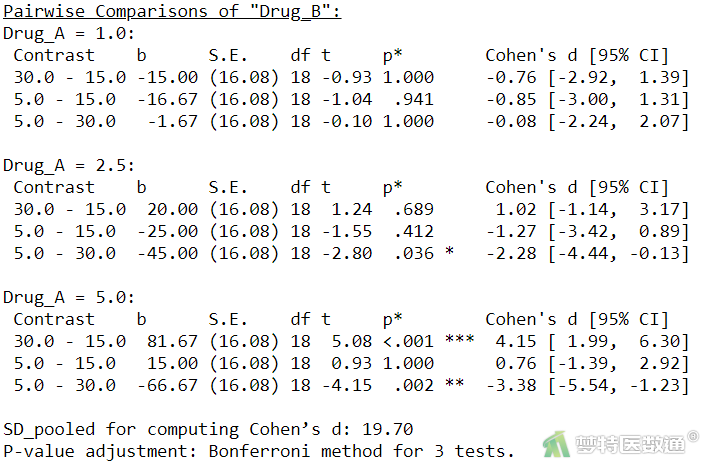
可知,当药物A为2.5 mg时,药物B浓度30.0 μg与5.0 μg相比,镇痛时间差异有统计学意义(P=0.036),30.0 μg与15.0 μg相比以及15.0 μg与5.0 μg相比差异均无统计学意义(P>0.05);当药物A为5.0 mg时,药物B浓度30.0 μg与15.0 μg相比,镇痛时间差异有统计学意义(P<0.001),30.0 μg与5.0 μg相比,镇痛时间差异有统计学意义(P=0.002),但15.0 μg与5.0 μg相比,镇痛时间差异无统计学意义(P=1.000)。
四、结论
本研究采用两因素方差分析探讨A、B两种镇痛药物联合运用在产妇分娩时的镇痛效果。通过对模型残差绘制箱线图提示,数据不存在异常值;通过Shapiro-Wilk检验,提示各组数据服从正态分布;通过Levene’s检验,提示数据总体方差相等;两药物之间存在交互作用(FDrug_A*Drug_B=5.073,P=0.006),故进行简单效应分析。
药物A在1.0 mg水平,药物B为5.0、15.0、30.0 μg水平时,镇痛时间分别为:83.333±20.207、100.000±18.028、85.000±10.000 min;药物A在2.5 mg水平,药物B为5、15、30 μg水平时,镇痛时间分别为:90.000±21.794、115.000±21.794、135.000±15.000 min;药物A在5.0 mg水平,药物B为5、15、30 μg水平时,镇痛时间分别为:110.000±21.794、95.000±27.839、176.667±15.275 min。
药物A的简单效应分析显示,在药物B为30.0 μg水平时,药物A各水平之间的镇痛时间差异有统计学意义(F=16.29,P<0.001)。但在药物B为5.0 μg和15.0 μg水平时,药物A各水平之间的镇痛时间差异均无统计学意义(P>0.05)。对药物A在药物B为30.0 μg水平时进行“Bonferroni (邦弗罗尼)”法两两比较结果显示, 1.0 mg至2.5mg时均值增加了50.00 min,至5.0 mg时均值增加了91.67 min,差异均有统计学意义(P<0.001);表明,在药物B为30.0 μg水平时,随着药物A浓度的增加,镇痛时间呈上升趋势。
药物B的简单效应分析显示,在药物A为1.0 mg水平时,药物B各水平之间的镇痛时间差异无统计学意义(F=0.65,P=0.533);但在药物A为2.5 mg和5.0 mg水平时,药物B各水平之间的镇痛时间差异均有统计学意义(P<0.05)。“Bonferroni (邦弗罗尼)”法两两比较显示,当药物A为2.5 mg时,药物B浓度30.0 μg与5.0 μg相比,镇痛时间差异有统计学意义(P=0.036),30.0 μg与15.0 μg相比以及15.0 μg与5.0 μg相比差异均无统计学意义(P>0.05)。当药物A为5.0 mg时,药物B浓度30.0 μg与15.0 μg相比以及30.0 μg与5.0 μg相比,镇痛时间差异均有统计学意义(P<0.01),但15.0 μg与5.0 μg相比,镇痛时间差异无统计学意义(P=1.000)。
综上可知,对产妇分娩时镇痛,A、B两种药物联合运用时会相互影响,随着药物浓度的增加,联合作用趋于复杂和不稳定。
五、分析小技巧
- 正态性检验:两因素或多因素方差分析时,有两种选择来测试正态性:如果每组有较多观察数,且组别较少时,可使用原始数据检查每个组的正态性。如果有很多组,或每个组的观察数很少,可使用残差检查整体的正态性。在jamovi中“ANOVA (方差分析)”模块下,“Shapiro-Wilk 检验”的结果即是对多组整体残差的正态性检验结果。关于正态性检验的注意事项详见文章正态性假设检验(Normality Hypothesis Test)——SPSS软件实现。
- 交互作用判断:两因素方差分析时,需要首先判断两个因素之间是否存在交互作用。如果交互作用有统计学意义,则需要分析单独效应。此时,单纯研究某个因素的作用并无意义,应分别探讨另一个因素不同水平时对该因素的作用。当不存在交互作用时,说明两因素的作用彼此独立,逐一分析各因素的主效应即可;计算主效应时,在模型中仍需要保留交互项。