有序Logistic回归分析(Ordinal Logistic Regression Analysis) ——jamovi软件实现

关键词：jamovi; 有序Logistic回归; 有序逻辑回归; 平行性检验; 比例优势检验

一、案例介绍

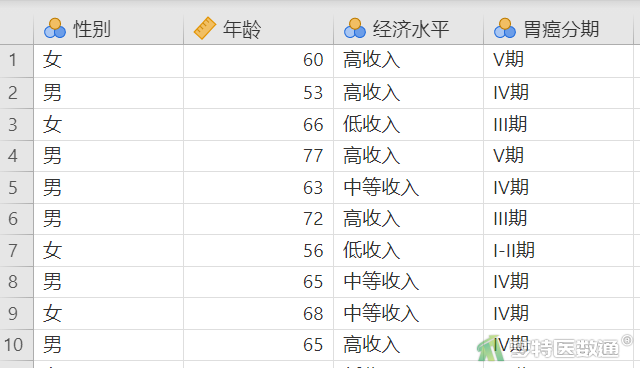
在某胃癌筛查项目中，为了确定胃癌筛查的重点人群，研究者想了解首诊“胃癌分期”与患者“经济水平”“性别”“年龄”之间的关系，试对数据进行分析。部分数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析

本案例的分析目的是探讨首诊“胃癌分期”与患者“经济水平”“性别”“年龄”之间的关系。在案例中，首诊“胃癌分期”为因变量，有Ⅰ~Ⅱ期、Ⅲ期、Ⅳ期、Ⅴ期4个分类，且分类间有等级次序关系。因此，可以采用有序Logistic回归模型进行分析。但需要满足以下5个条件：

条件1：因变量唯一，且为有序多分类变量。本研究中因变量只有“胃癌分期”，且为有序多分类变量。该条件满足。

条件2：存在一个或多个自变量。本研究中有3个自变量，“经济水平”“性别”为分类变量，“年龄”为连续变量，该条件满足。

条件3：观察变量相互独立。本研究中各研究对象的观察变量都是独立的，不存在互相干扰的情况，该条件满足。

条件4：自变量之间无多重共线性，该条件需要通过软件分析后判断。

条件5：满足平行性，该条件需要通过软件分析后判断。

有序Logistic回归模型分析结果除了常数项不同，各模型的自变量系数都相同。平行性检验的目的即是验证自变量不同取值对因变量的影响系数是否相同，即要满足无论因变量的分割点在什么位置，模型中各个自变量对因变量的影响不变。

如果不满足平行性假设，则考虑使用无序多分类Logistic回归或用不同的分割点将因变量变为二分类变量，分别进行二项Logistic回归。但是，当样本量过大时，平行线检验会过于敏感。即当存在平行性时，也会显示P<0.05。此时，可以尝试将因变量设置为哑变量，并拟合多个二项Logistic回归模型，通过观察自变量对各哑变量的OR值是否近似来判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件4判断(多重共线性判断)

(1) 软件操作

jamovi中有序Logistic回归模块尚无检测共线性的选项，但可以通过多重线性回归分析实现共线性的诊断，操作详见多重线性回归分析(Multiple Linear Regression Analysis)——jamovi软件实现。结果见图2。

(2) 结果解读

共线性分析结果见图2。由“年龄”“性别”“经济水平”的方差膨胀因子(VIF)分别为1.016、1.007和1.008，提示自变量之间无严重多重共线性，满足分析条件。若存在严重多重共线性，处理方法参照多因素二项Logistic回归。

2. 条件5判断(平行性检验)

(1) 软件操作

①选择“分析”—“R”—“Rj Editor+ (R语言jamovi编辑器+)”(图3)。

②在Rj Editor中，有两个版本的R语言可供选择，即jamovi自带的版本(jamovi R)和已经安装的R语言(System R)，此处选择后者，Output (输出)选择Show code and output (输出代码和结果)(图4)。

③在R软件中安装“VGAM”包和“jmvconnect”包。

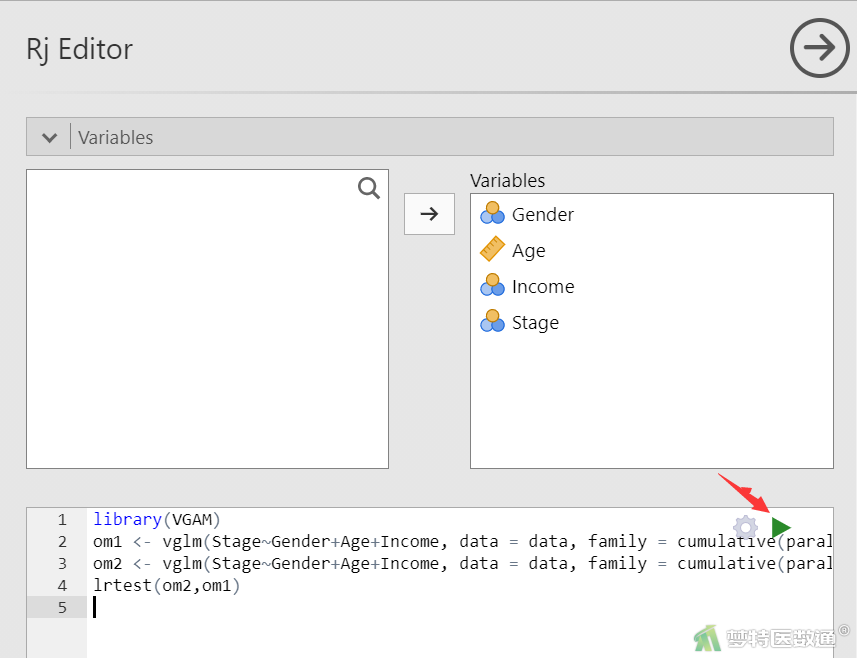
④输入下方程序代码，然后点击图5右边绿色三角形按钮运行程序(此处需要注意的是，要将变量名更改为英文，中文会报错)。

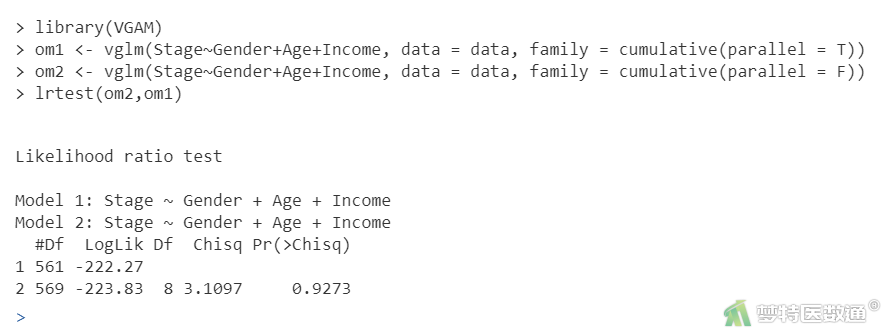
library(VGAM)
om1 <- vglm(Stage~Gender+Age+Income, data = data, family = cumulative(parallel = T))
om2 <- vglm(Stage~Gender+Age+Income, data = data, family = cumulative(parallel = F))
lrtest(om2,om1)

(2) 结果解读

模型的平行性检验结果见图6。平行性检验的原假设是各回归方程互相平行，χ²=3.1097，P=0.9273>0.05接受原假设，说明平行性假设成立，即各回归方程相互平行，满足条件5。

(二) 变量筛选

(1) 软件操作

①选择“分析”—“回归”，在“逻辑回归”中选择“有序分类结局”；将因变量“胃癌分期”选入“因变量”，将连续变量“年龄”选入“协变量”，将分类变量“性别”“经济水平”选入“因子”，见图7。

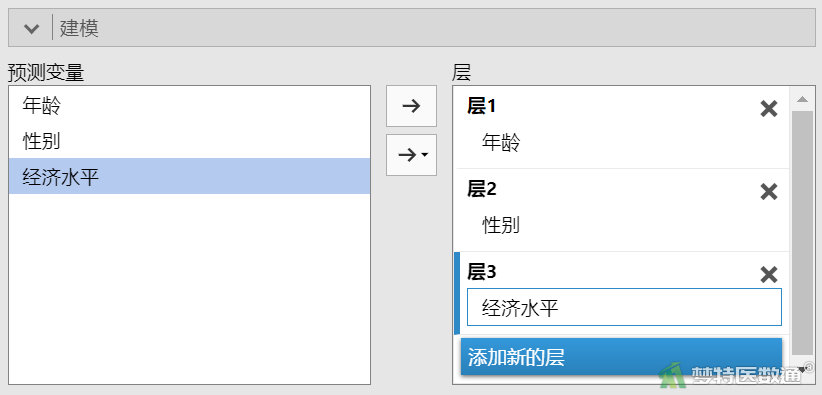
②在“建模”中，分别按次序为每个自变量创建一个“层”，并将自变量选入层中，本案例需要创建3个层，见图8。

③在“参考水平”下，为分类变量选择合适的参考水平，“性别”参考水平设置为“男性”，“经济水平”参考水平设置为“低收入”(图9)。

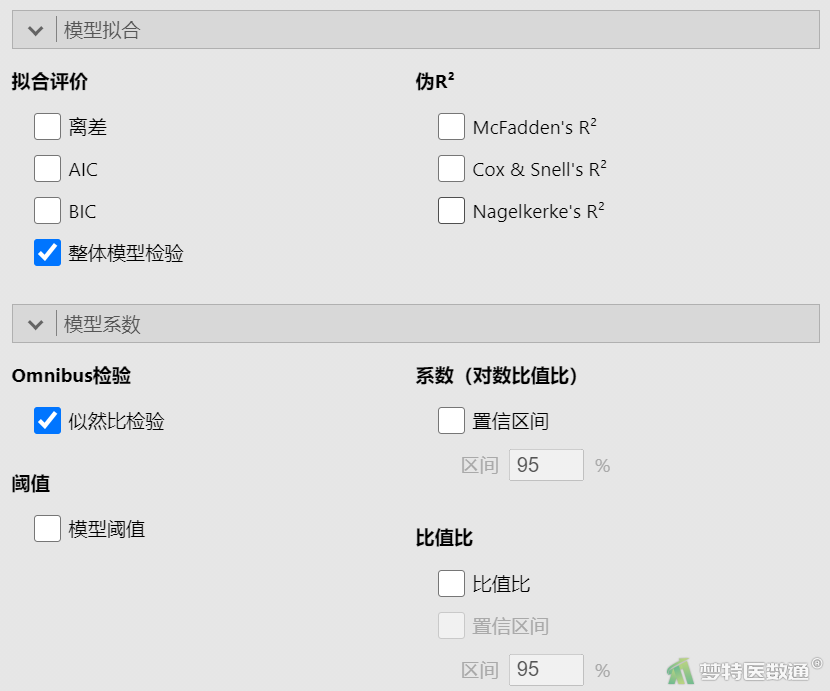
④在“模型拟合”下(图10)的“拟合评价”中勾选“整体模型检验”，结果见表1；在“模型系数”下的“Omnibus检验”中勾选“似然比检验”，结果见表2。

(2) 结果解读

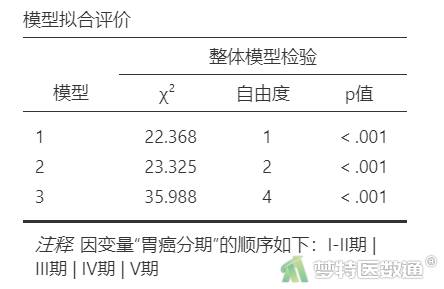
由于本案例分析过程中创建了3个块，所以一共会生成3个模型。“模型拟合评价”结果(表1)分别显示了每个模型的检验结果，可见所有模型均有统计学意义，说明所有模型中都至少存在一个自变量具有统计学意义。

“Omnibus似然比检验”结果(表2)中列出了每个自变量在模型中是否有统计学意义，即是否应被纳入模型。可知，“性别”无统计学意义，应该被移除模型。

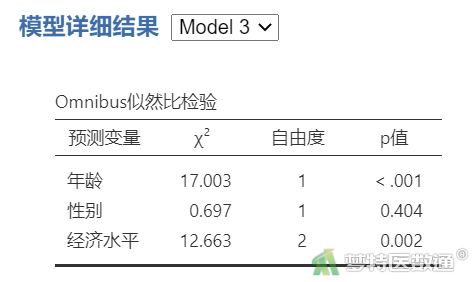
“模型对比”结果(表3)中列出了每个模型新增一个自变量后与上一个模型相比差异是否有统计学意义，也即表示新加入的变量是否有统计学意义。可知，模型2与模型1相比差异无统计学意义，说明第2个块中的变量无统计学意义，即变量“性别”无统计学意义。

(三) 模型拟合

将“性别”及其“层”从“建模”中移除后进行如下操作。

1. 软件操作

勾选“模型拟合”和“模型系数”下的所有选项(图11)。

2. 结果解读

(1) 拟合优度

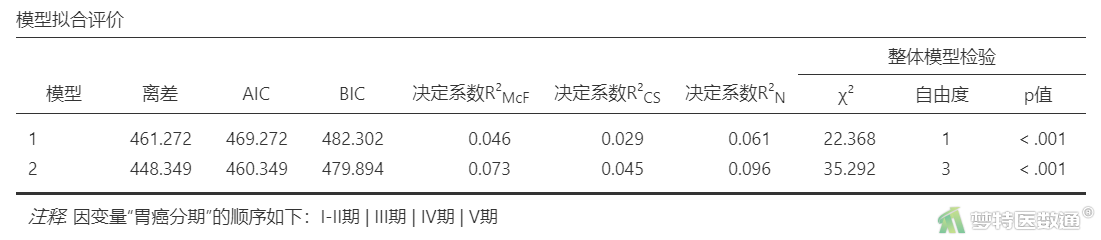
“模型拟合评价”结果(表4)，列出了2个模型的Deviance (残差)、AIC (赤池信息量准则)、BIC (贝叶斯信息准则)、R²_McF、R²_CS、R²_N和Overall Model Test (模型整体检验)。

AIC和BIC均是衡量统计模型拟合优良性(Goodness of fit)的一种标准，其值越小越好。

R²_McF、R²_CS、R²_N均说明的是回归方程对解释变量变异量化的一种反映，越接近1说明回归方程的拟合度越高。R²_McF介于0.2~0.4之间代表模型拟合的较好，因此本数据集模型拟合度不高。

Overall Model Test (模型整体检验)采用的是似然比卡方检验对模型进行参数检验，考察模型的整体显著性，可见2个模型均有统计学意义，表示2个模型中均至少有1个自变量具有统计学意义。

(2) 模型系数

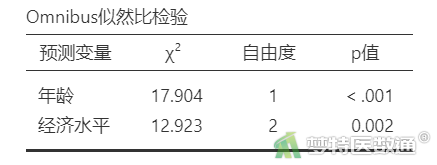
“模型对比”结果(表5)和“Omnibus似然比检验”结果(表6)显示，模型2中所有自变量均有统计学意义。

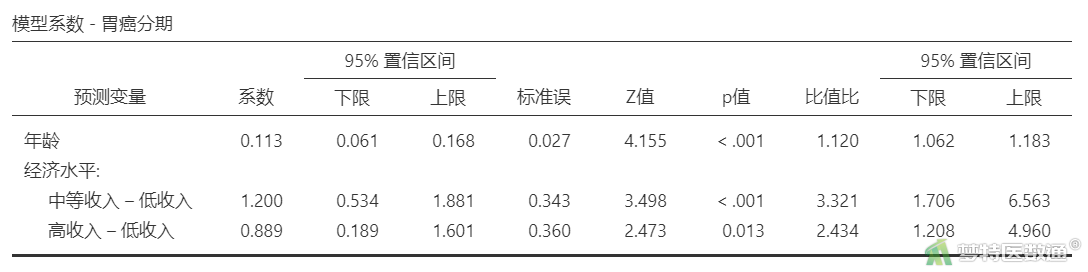
“模型系数 – 胃癌分期”结果(表7)列出了各自变量拟合后在模型2中的系数(回归系数)及其95%CI、SE (标准误)、Z (统计量)、P (P值)、比值比 (OR值)及其95%CI。

其中“年龄”的P<0.001，有统计学意义；OR=1.120 (95%CI 1.062~1.183)，表示年龄每增加1岁，其首诊“胃癌分期”提升一个等级的可能性是原来的1.120倍。“中等收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的3.321倍(95%CI 1.706~6.563，P<0.001)；“高收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的2.434倍(95%CI 1.208~4.960，P=0.013)。

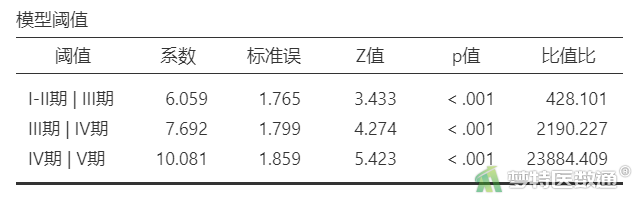
“模型阈值”结果(表8)列出了各个模型的常数项，由于因变量有4个水平，共生成4-1=3个模型。

四、结论

本研究采用有序Logistic回归模型分析首诊“胃癌分期”与患者“经济水平”“性别”“年龄”之间的关系。因变量例数分布满足样本量需求，变量之间不存在严重共线性，满足平行性假设(χ²=3.120，P=0.927)。

“性别”对首诊“胃癌分期”的影响无统计学意义。“年龄”每增加1岁，其首诊“胃癌分期”提升一个等级的可能性是原来的1.120倍(95%CI 1.062~1.183，P<0.001)。“中等收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的3.321倍(95%CI 1.706~6.563，P<0.001)；“高收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的2.434倍(95%CI 1.208~4.960，P=0.013)。所建立的模型有统计学意义(χ²=35.292，P<0.001)。