无序多分类Logistic回归(Multinomial Logistic Regression Analysis) ——jamovi软件实现

关键词：jamovi; 无序多分类logistic回归; 无序logistic回归; 无序逻辑回归

一、案例介绍

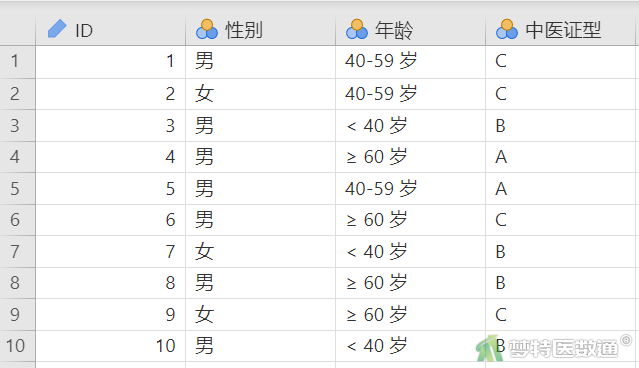
欲探索性别(男、女)与年龄(岁，<40、40~59、≥60)是否对某中医证型(A、B、C)的分类有影响，从医院数据库中随机选择了200例样本进行分析。部分数据见图1，本案例数据可从“附件下载”处下载。

二、问题分析

本案例中，因变量“中医证型”为无序多分类变量，欲探索“性别”与“年龄”是否对“中医证型”分类有影响，可将“中医证型”的某一类别设置为对照组，通过无序多分类logistic回归分析将另外两种不同类别证型的样本分别与对照组进行对比，得到“性别”“年龄”与这两种类别证型的暴露−风险关系。无序多分类logistic回归需要满足3个条件：

条件1：因变量唯一，且为无序多分类变量。本案例符合。

条件2：存在一个或多个自变量，可为定性与定量变量。本案例符合。 条件3：一般要求例数较少类的样本量为自变量个数的10~15倍(EPV原则)且经验上每组的人数最好多于30例，参照水平组不应少于30或50例。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件3判断(因变量样本例数)

(1)软件操作

①选择“分析”—“探索”—“描述”，将因变量“中医证型”选入右侧“变量”框，并勾选“频数表”(图2)，结果见表1。

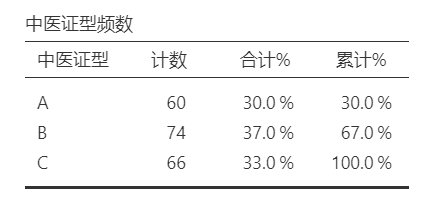
(2)结果解读

“中医证型频数”结果(表1)显示，，中医证型A、B、C3组例数分别为60、74、66例，均>30例。根据条件3，本案例可纳入4~6个自变量进行多因素无序多分类logistic回归分析。

2. 条件3判断(自变量样本例数)

逐一计算分类变量各类别的因变量例数。

(1) 软件操作

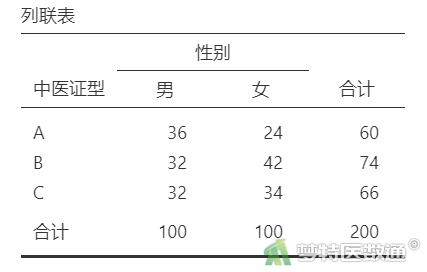
①选择“分析”—“频数”—“独立样本χ²关联检验”；将变量“中医证型”选入“行”，“性别”选入“列”(图3)，结果见表2。

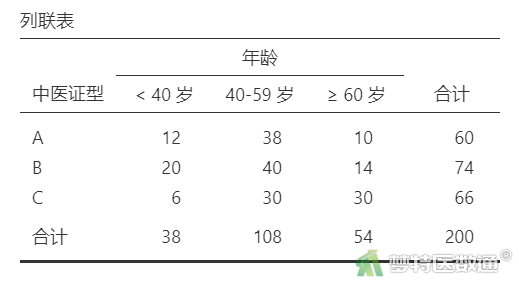
②参照上述操作，考察“年龄”的频数分布情况，结果见表3。

(2) 结果解读

“列联表”结果(表2、表3)显示，“年龄”水平在“<40岁”和“≥60岁”条件下因变量的例数≤30，如果“年龄”在多因素分析过程中进入模型，应注意避免例数较少的水平被选为参照，若实在不能避免，在结果解释时应注意其局限性。

(二) 变量筛选

(1) 软件操作

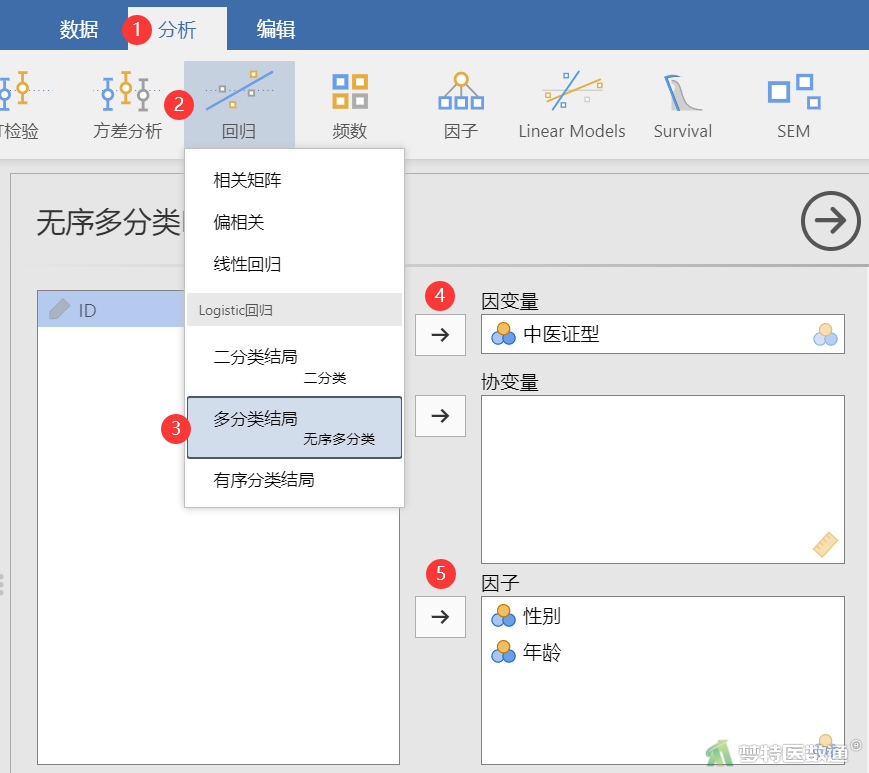
①选择“分析”—“回归”，在“Logistic回归”中选择“多分类结局(无序多分类)”；将因变量“中医证型”选入“因变量”，将分类变量“性别”“年龄”选入“因子”(图4)。若有连续变量则选入“协变量”。

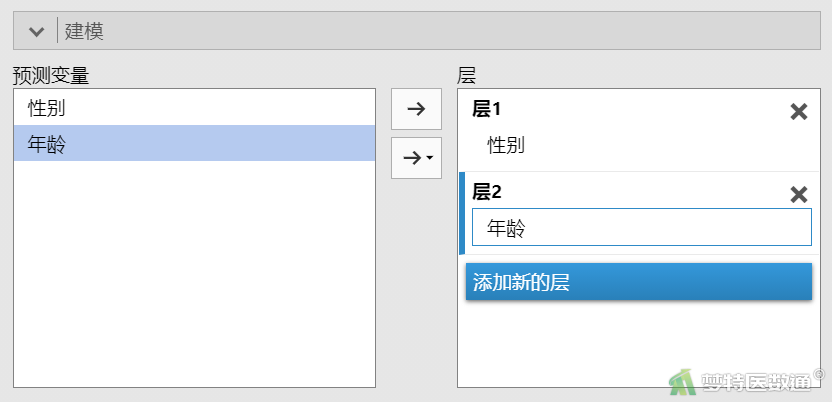
②在“建模”中，分别按次序为每个自变量创建一个“层”，并将自变量选入层中，本案例需要创建2个层(图5)。

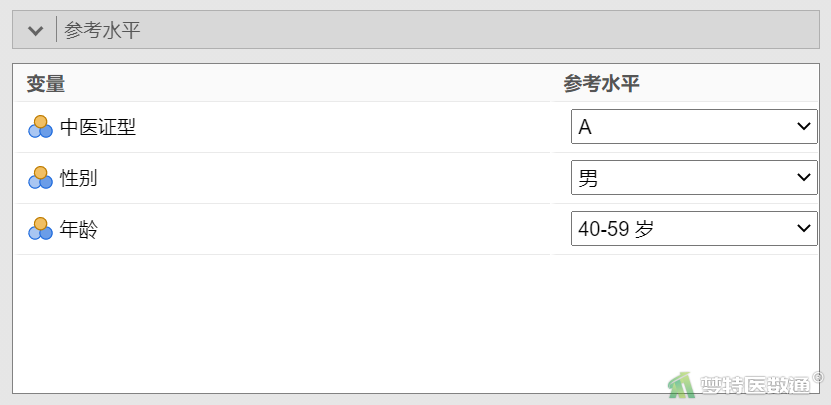
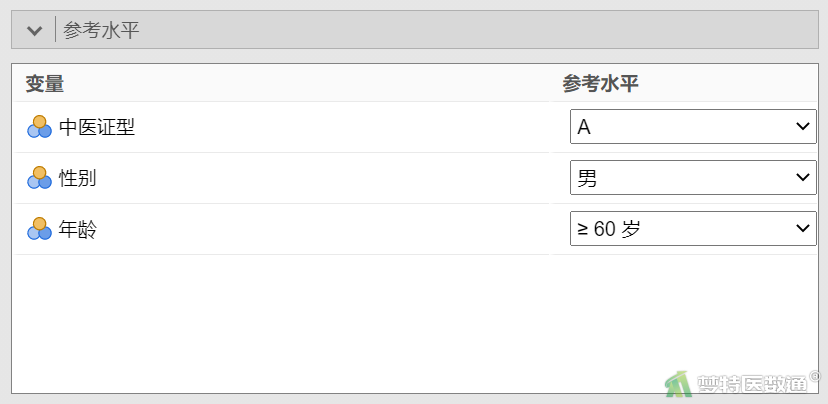
③在“参考水平”下，为分类变量选择合适的参考水平，根据条件3(自变量样本例数)计算结果，“年龄”水平为“＜40岁”和“≥60岁”时因变量的例数≤30，如果“年龄”在多因素分析过程中进入模型，应注意避免例数较少的水平被选为参照(图6)。

④在“模型拟合”下的“拟合评价”中勾选“整体模型检验”(图7)，结果见表4；在“模型拟合”下的“Omnibus检验”中勾选“似然比检验”(图7)，结果见表5。

(2) 结果解读

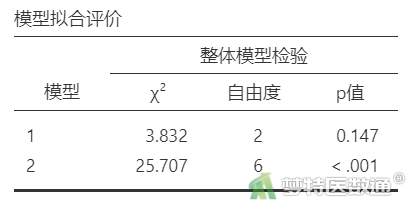
由于本案例分析过程中创建了2个块，所以一共会生成2个模型(层次回归分析)。“模型拟合评价”结果(表4)分别显示了每个模型的检验结果，可见模型1无统计学意义，模型2有统计学意义，说明模型2中至少存在一个自变量具有统计学意义。模型1中只有一个自变量“性别”，也表明该自变量没有统计学意义。

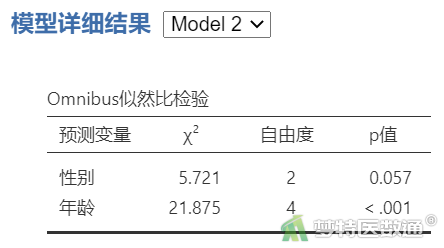
“Omnibus似然比检验”结果(表5)中列出了每个自变量在模型中是否有统计学意义，即是否应被纳入模型。结果显示“性别”无统计学意义，应该被移除模型。但考虑到本案例只有2个自变量，且“性别”的P值比较接近0.05，此次分析过程中仍然保留在多因素分析模型中。

“模型比较”结果(表6)中列出了模型1新增一个自变量后与原模型相比差异是否有统计学意义，也即表示新加入的变量是否有统计学意义。结果显示模型2与模型1相比差异有统计学意义，说明第2个块中的变量有统计学意义，即变量“年龄”有统计学意义。可见，表6与表5等价。

(三) 模型拟合

1. 软件操作

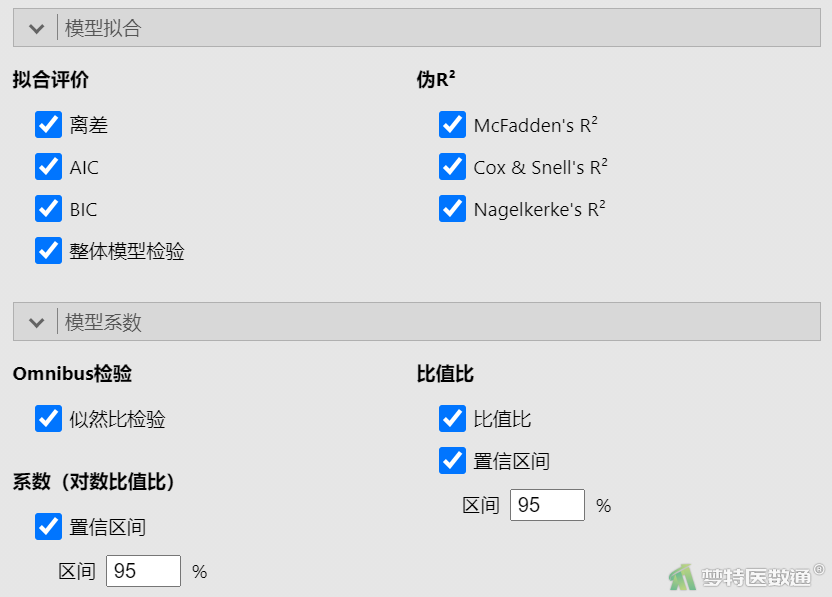
①勾选“模型拟合”和“模型系数”下的所有选项(图8)。

②先选择“性别”的参照水平为“男”，“年龄”的参照水平为“≥60岁”(尽管“≥60岁”水平的例数<30，此处为了演示更多有统计学意义的结果，仍选择该水平为参照)。“中医证型”的参照水平先选择为“A”，即分析结果为B与A对比的情况、C与A对比的情况，结果见表8。再选择“中医证型”的参照水平先选择为“C”，即分析结果为A与C对比的情况、B与C对比的情况，结果见表9。

2. 结果解读

“模型拟合评价”结果(表7)列出了2个模型的“Deviance (残差)”“AIC (赤池信息量准则)”“BIC (贝叶斯信息准则)”“R²_McF”“R²_CS”“R²_N”和“Overall Model Test (模型整体检验)”。

AIC和BIC均是衡量统计模型拟合优良性(Goodness of fit)的一种标准，其值越小越好。“R²_McF”“R²_CS”“R²_N”均说明的是回归方程对解释变量变异量化的一种反映，越接近1说明回归方程的拟合度越高。“R²_McF”介于0.2~0.4之间代表模型拟合的较好，因此本数据集模型拟合度不高。“Overall Model Test (模型整体检验)”采用的是似然比卡方检验对模型进行参数检验，考察模型的整体显著性，可见模型2有统计学意义，表示该模型中至少有1个自变量具有统计学意义。

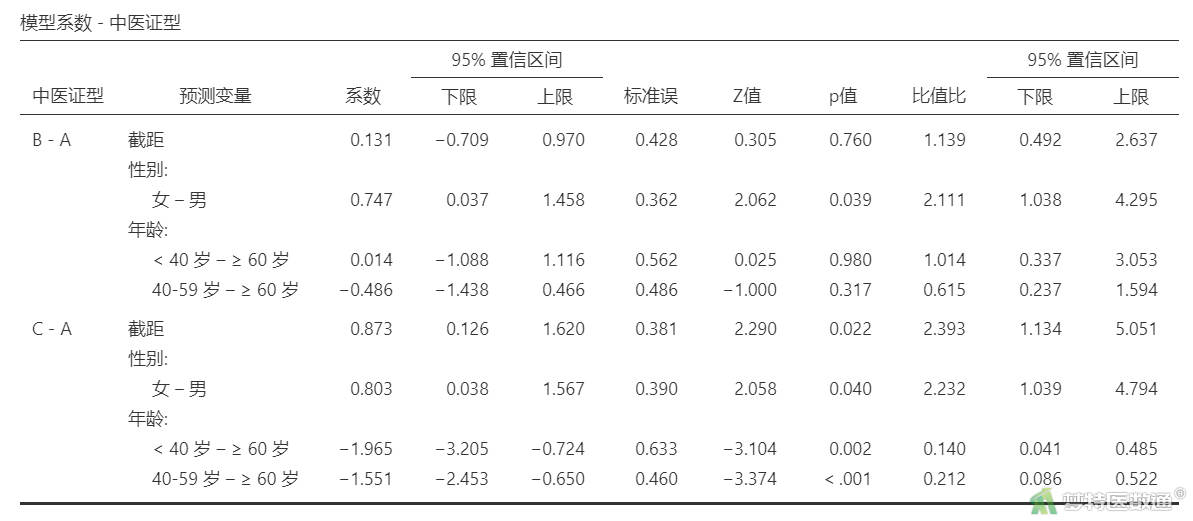
“模型系数−中医证型”结果(表8)列出了“中医证型”B与A比较、C与A比较各自变量拟合后在模型2中的“Estimate(回归系数)”及其95%CI、“SE (标准误)”“Z (统计量)”“P (P值)”“比值比 (OR值)”及其95%CI。可知，在“中医证型”B与A比较中，年龄无统计学意义。在“中医证型”C与A比较中，年龄<40岁的患者出现C型的风险比年龄≥60岁的低86.0% (OR=0.140，95%CI 0.041~0.485；P=0.002)，年龄40~59岁的患者出现C型的风险比年龄≥60岁的低78.8% (OR=0.212，95%CI 0.086~0.522；P<0.001)。

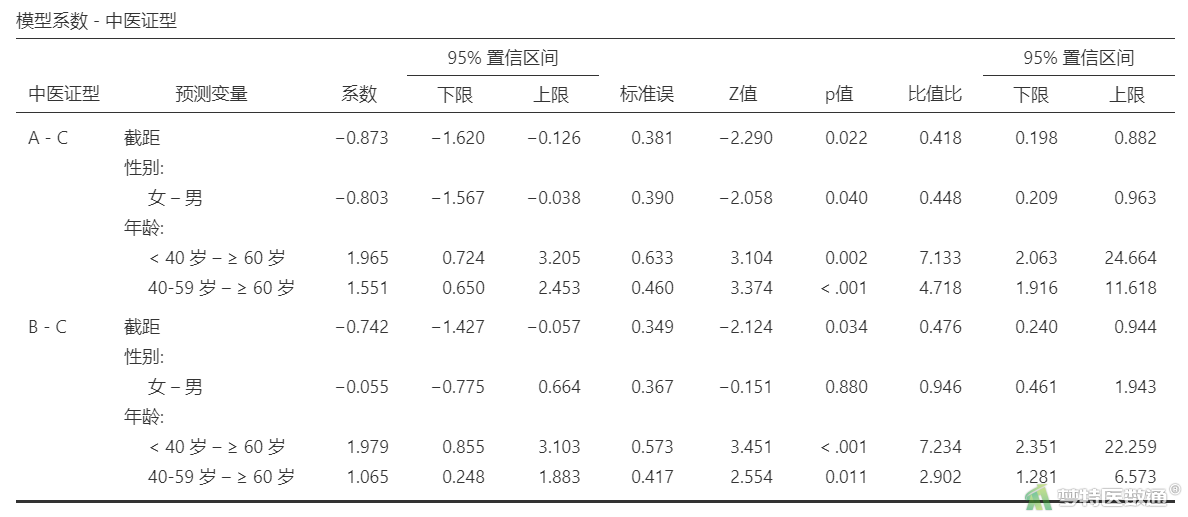
“模型系数−中医证型”结果(表9)显示，在“中医证型”B与C比较中，年龄<40岁的患者出现B型的风险是年龄≥60岁的7.234倍 (95%CI 2.351~22.259；P<0.001)，年龄40~59岁的患者出现B型的风险是年龄≥60岁的2.902倍 (95%CI 1.281~6.573；P=0.011)。“中医证型”A与C的比较结果(表9)与C与A的比较结果(表8)等价。

四、结论

本研究采用无序多分类Logistic回归探讨性别和年龄是否对某中医证型的分类有影响。因变量例数分布满足样本量需求。 “Omnibus整体似然比检验”表明，自变量“性别”在模型中无统计学意义(χ²=5.721，P=0.057)，“年龄”在模型中有统计学意义(χ²=21.875，P<0.001)。在“中医证型”B与A比较中，年龄无统计学意义。在“中医证型”C与A比较中，年龄<40岁的患者出现C型的风险比年龄≥60岁的低86.0% (OR=0.140，95%CI：0.041~0.485；P=0.002)，年龄40~59岁的患者出现C型的风险比年龄≥60岁的低78.8% (OR=0.212，95%CI：0.086~0.522；P<0.001)。在“中医证型”B与C比较中，年龄<40岁的患者出现B型的风险是年龄≥60岁的7.234倍 (95%CI 2.351~22.259；P<0.001)，年龄40~59岁的患者出现B型的风险是年龄≥60岁的2.902倍 (95%CI 1.281~6.573；P=0.011)。

五、知识小贴士

• 无序多分类logistic回归的因变量为多分类变量，内部分析过程是选择一个参照组将因变量拆分为多个二分类变量，拟合多个二项logistic回归。

• 由于无序多分类logistic回归的本质是多个二项logistic回归，因此其结果解读可参考二项logistic回归，只是每个变量需要在多个二项logistic回归中分别解读。

• 在“中医证型”B与C的比较中，可发现自变量“性别”有统计学意义，但由于整体检验该变量并无统计学意义，因此尚不能认为“性别”对中医证型的分类有影响。