多重线性回归分析(Multiple Linear Regression Analysis)——MedCalc软件实现

关键词：MedCalc; 多重线性回归; 多元线性回归; 多重共线性; 自变量选择; 逐步回归; 模型拟合评价

一、案例介绍

某社区医师从本社区的糖尿病患者中随机抽取50例，收集了他们的性别(Gender，0=女、1=男)、空腹胰岛素(Fasting insulin，mmol/L)、糖化血清蛋白(Glycosylated serum protein，mmol/L)和空腹血糖(FBS，mmol/L)，欲探究空腹血糖是否受到这几项指标的影响。部分数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析

本案例的目的是分析空腹血糖是否受到其他几项指标的影响，由于因变量是定量资料，初步考虑可使用多重线性回归分析。但需要满足以下7个条件：

条件1：样本量是自变量个数的5~10倍。本案例有4个自变量，样本量为50，满足该条件。

条件2：自变量若为连续变量，需要与因变量之间存在线性关系，可通过绘制散点图予以考察。

条件3：各观测行间相互独立。对研究设计和数据收集的过程进行分析，可判断本案例中观测值之间不存在互相影响的情况。满足该条件。

条件4：不存在显著的多变量异常值，该条件需要通过软件分析后判断。

条件5：自变量之间无多重共线性，该条件需要通过软件分析后判断。

条件6：残差符合正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件7：残差大小不随所有变量取值水平的变化而变化，即方差齐性，可通过绘制残差图进行判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件2判断(线性关系判断)

检验因变量与连续性自变量之间是否存在线性关系，可通过绘制每个自变量和因变量的散点图进行判断。

(1) 软件操作

①选择“统计”—“相关—“散布图”（应译为“散点图”，为和软件保持一致，本文操作中写为“散布图”）(图2)。

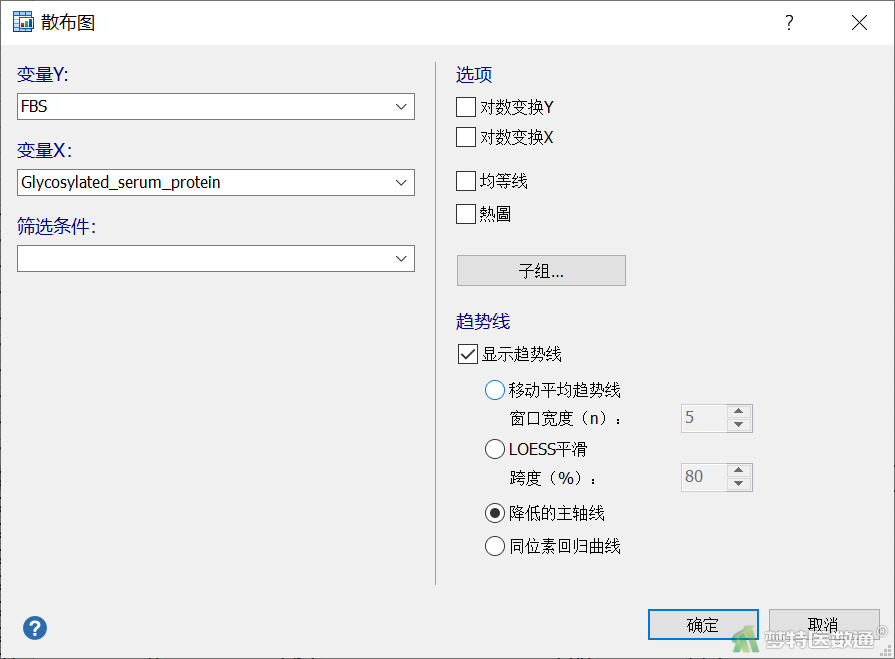
②在“散布图”对话框(图3)中，“变量Y”中选择FBS，“变量X”中选择Glycosylated serum protein，勾选“显示趋势线”——“降低的主轴线”，点击“确定”即可得到糖化血清蛋白(Glycosylated serum protein)和空腹血糖(FBS) 之间的散点图(图4)。

③ 参照步骤②绘制自变量“空腹胰岛素(Fasting insulin)”与因变量“空腹血糖(FBS)”的散点图(图5)。

(2) 结果解读

由图4可知，糖化血清蛋白与空腹血糖之间存在线性关系。由图5可知，空腹胰岛素与空腹血糖之间存在线性关系。每个自变量和因变量的线性关系只是针对自变量为连续变量而言的，因此本例中分类自变量与因变量之间的线性关系可以忽略。综上，本案例满足条件2。

2. 条件4判断(异常值检测)

(1) 软件操作

选择“统计”—“异常值检测”(图6)。

以自变量“糖化血清蛋白(Glycosylated serum protein)”的异常值检验为例：在“异常值检测”对话框的“变量”中选择Glycosylated serum protein，其他设置保持默认(图7)。其他自变量的异常值检测步骤和结果此处不一一描述(请读者自行操作、查看)。

(2) 结果解读

糖化血清蛋白的异常值检验结果(图8)显示，并无疑似异常值。

其他连续自变量的的异常值检验操作同上，结果均未发现需要特殊处理的异常值。

3. 条件5判断(多重共线性诊断)

(1) 软件操作

①选择“统计”—“回归”—“多元回归”(图9)。

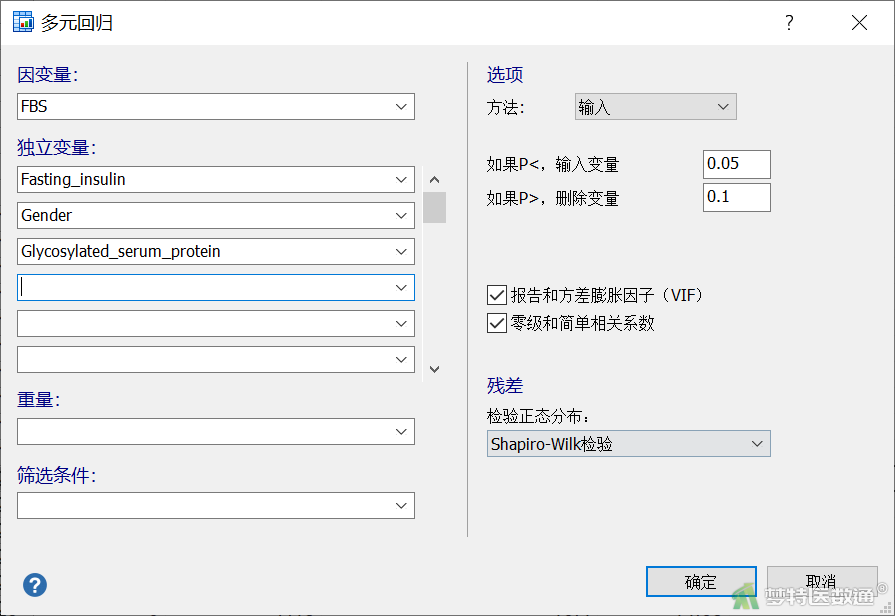
②在弹出的对话框中，“因变量”中选择FBS，“独立变量”中依次选择Fasting insulin、Gender和Glycosylated serum protein，其他选项保持默认，点击“确定”(图10)。

(2) 结果解读

多重共线性诊断结果(图11)显示，方差膨胀因子(VIF)均小于5，提示自变量之间不存在多重共线性(一般VIF大于5，则提示有共线性存在。若数据存在多重共线性，需用复杂的方法进行处理，其中最简单的方法是剔除引起共线性的因素之一，根据知识与理论决定剔除哪一个因素)。

4. 条件6~7判断

在条件5判断的“多元回归”结果的最后可以看到“保存预测值”和“保存残差”两个操作(图12)。

点击“保存预测值”，打开“保存预测值”对话框(图13)，选择保存在“E”列，标题为“MREGR_Pred1”，勾选“标准化”，点击“确定”。

再点击“保存残差”，打开“保存残差”对话框(图14)，选择保存在“F列”，标题为“MREGR_Pesid1”，勾选“标准化”，点击“确定”。

(1) 正态性判断

选择“统计”—“分布图”—“正态图”(图15).

在“正态图”对话框(图16)中，“变量”中选择之前保存的残差变量MREGR_Pesid1，勾选“Q-Q图”，点击“确定”。

Q-Q图见图17，可以看到分布图近似于正态分布，可见标准化残差近似服从正态分布，本案例满足条件6。

(2) 方差齐性判断

可通过回归模型的标准化残差与标准化预测值的散点图来判断方差齐性。

选择“统计”—“相关”—“散布图”(图18)。

在“散布图”对话框(图19)中，“变量Y”中选择标准化残差MREGR_ Resid1，“变量X”中选择MREGR_Ped1，点击“确定”。

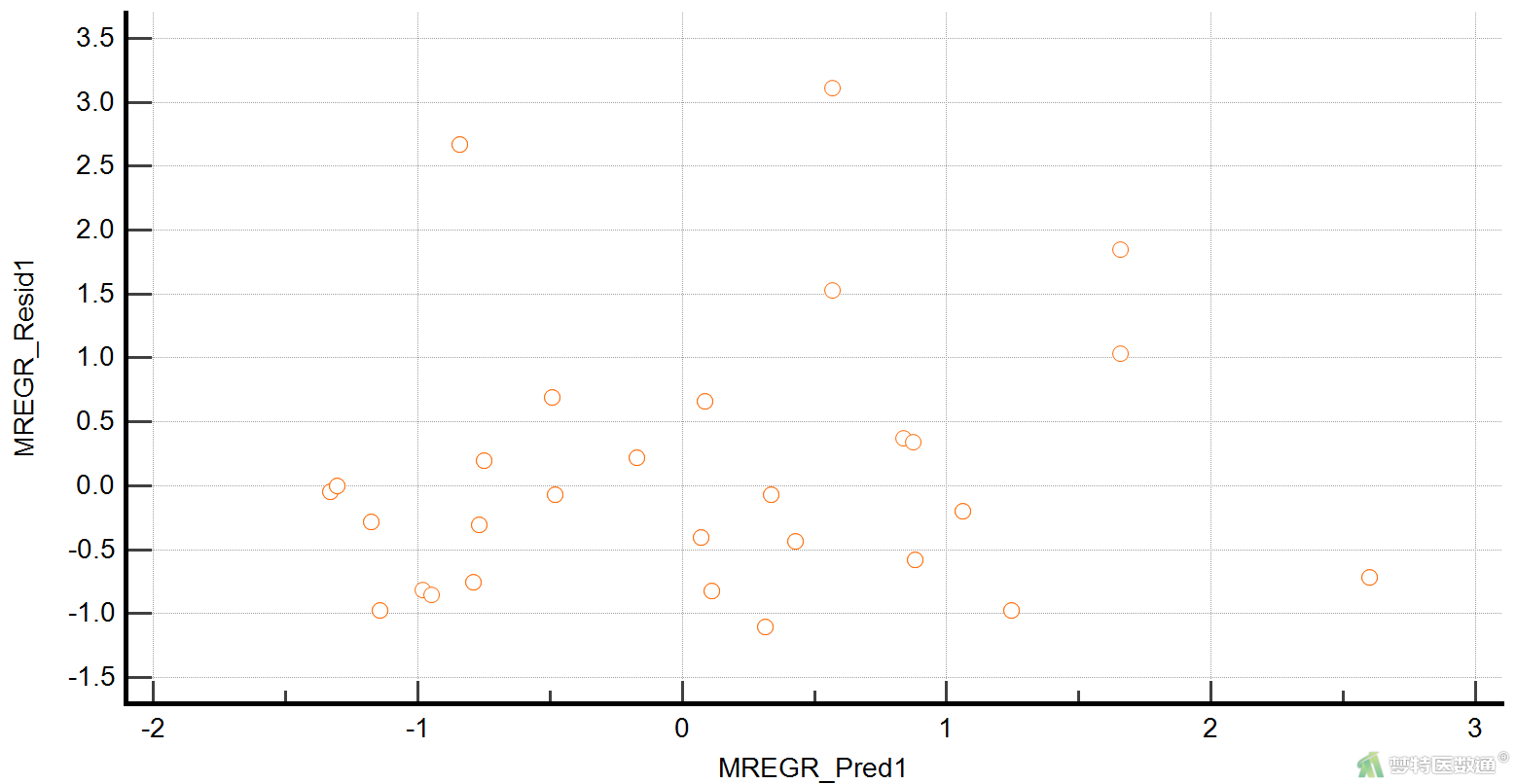
散点图(图20)显示，预测值和对应的残差分布较为均匀，数据点均分布在±3个标准差之内，并未出现特殊的分布形式(如漏斗或者扇形)，提示残差的方差齐，满足条件7。

(二) 变量筛选

从图11列出的结果可知，自变量Gender的t=-0.100，P=0.9206，无统计学意义，可移除模型。

①选择“统计”—“回归”—“多元回归”(图9)。

②在“多元回归”对话框(图21)中，“因变量”中选择FBS，“独立变量”中依次选择Fasting insulin和Glycosylated serum protein，其他选项保持默认，点击“确定”。

(三) 模型拟合优度

方差分析结果(图22)显示，F=24.6695，P<0.0001，提示模型有统计学意义。如果P>0.05，则说明回归模型无统计学意义。

模型的拟合程度和模型统计检验结果(图23)显示，R²=0.5121，提示自变量可以解释51.21%的因变量变异；调整R²=0.4914，提示自变量可以解释49.14%的因变量变异（R²为决定系数，用来反映模型预测的准确性；但是R²会受自变量个数的影响，夸大自变量对因变量变异的解释程度，自变量越多，R²越大。为校正自变量个数的影响，一般采用后面的调整R²）。

(四) 回归系数解释

回归方程结果见图24，其列出了截距和自变量的回归系数及回归系数95%CI、t值及P值。结果显示，回归模型的截距为8.1265，表示自变量取值为0时，因变量的取值，并无实际专业意义。空腹胰岛素(Fasting_insulin)的非标准化系数(即斜率)为-0.1131 (95%CI -0.2613~0.1891；P=0.0698)，表示空腹胰岛素每增加1mmol/L，空腹血糖减少0.1131 mmol/L，但变化无统计学意义(P=0.0698)；糖化血清蛋白(Glycosylated_serum_protein)的非标准化系数(即斜率)为0.7097 (95%CI 0.6681~0.6272；P<0.001) ，表示糖化血清蛋白每增加1 mmol/L，空腹血糖增加0. 7097 mmol/L。

据此可以写出本案例的回归方程为：

空腹血糖 = 8.1265- 0.1131×空腹胰岛素 + 0.7097×糖化血清蛋白。

根据此方程输入相关自变量数值即可对空腹血糖进行预测。

四、结论

本研究采用多重线性回归模型考察空腹血糖是否受到性别、空腹胰岛素和糖化血清蛋白的影响。通过绘制散点图，发现空腹胰岛素和糖化血清蛋白与空腹血糖之间存在线性关系。通过异常值检测，发现数据不存在需要特殊处理的异常值。通过多重线性回归判断自变量之间不存在严重多重共线性。通过绘制标准化残差的Q-Q图，发现残差服从正态分布。通过绘制标准化预测值和标准化残差的散点图，提示残差方差齐。因此判断本案例满足多重线性回归分析条件。

多重线性回归分析显示，在其他变量不变的情况下，“空腹胰岛素”每增加1 mmol/L，空腹血糖减少0.1131mmol/L (95%CI -0.2613~0.1891)，但变化无统计学意义(P=0.0698)；“糖化血清蛋白”每增加1 mmol/L，空腹血糖增加0. 7097 mmol/L (95%CI 0.6681~0.6272；P<0.001)

线性回归方程为：空腹血糖 = 8.1265- 0.1131×空腹胰岛素 + 0.7097×糖化血清蛋白。回归模型具有统计学意义，F=24.6695，P<0.001；模型可以解释49.14%的因变量的变异(调整 R²=0.4914)。