多重线性回归分析(Multiple Linear Regression Analysis)——理论介绍

关键词：多重线性回归; 多元线性回归; 多重共线性; 自变量选择; 逐步回归; 模型拟合评价

一、适用条件

多重线性回归分析，一般需要满足以下7个条件：

条件1：样本量至少应是自变量个数的5~10倍。

条件2：自变量若为连续变量，需要与因变量之间存在线性关系，可通过绘制散点图予以考察。

条件3：各观测值之间相互独立，即残差之间不存在自相关。

条件4：不存在显著的多变量异常值。

条件5：自变量之间无多重共线性。

条件6：残差符从正态(或近似正态)分布。

条件7：残差大小不随所有变量取值水平的变化而变化，即方差齐性。

二、多重线性回归模型

多重线性回归模型(Multiple Linear Regression Model)即描述因变量Y如何随多个自变量X的改变而改变。假定对n例观察对象逐一测定了因变量Y与m个自变量X₁、X₂、…、X_m的数值，多重线性回归模型的一般形式为

\(\mathrm{Y}=\beta_{0}+\beta_{1} X_{1}+\beta_{2}X_{2}+\cdots+\beta_{m} X_{m}+e\)

式中β₀为常数项，又称截距。β₁、β₂，…，β_m称为偏回归系数(partial regression coefficient)或简称回归系数。该式表示数据中应变量Y可以近似地表示为自变量X₁、X₂、…、X_m的线性函数。e则是去除m个自变量对Y的影响后的随机误差(即残差)。偏回归系数β_j (j=1、2、…、m)表示在其他自变量保持不变时，X_j变化一个单位时Y的平均变化量。

多重线性回归分析一般可分为两个步骤：

(一) 拟合多重线性回归方程

根据样本数据对模型参数β₁、β₂、…、β_m进行估计，从而得到多重线性回归方程，即

\(\hat{Y}=b_{0}+b_{1} X_{1}+b_{2} X_{2}+\cdots+b_{m}X_{m}\)

其中，b₀、b₁、b₂、…、b_m为模型参数的估计值，\(\widehat{Y}\)为Y的估计值，表示在一组自变量X₁、X₂、…、X_m取值时Y的平均值。

与简单直线回归相同，多重线性回归模型的参数估计可以由最小二乘法(least sum of squares，LS)得到，即根据观察到的n例数据，使残差平方和达到最小，即

\(\mathrm{Q}=\sum_{k=1}^{n}\left(Y_{k}-\hat{Y}_{k}\right)^{2}=\sum_{k=1}^{n}\left[Y_{k}-\left(b_{0}+b_{1}X_{1 k}+b_{2} X_{2 k}+\cdots+b_{m} X_{mk}\right)\right]^{2}\)

数学上可通过方程组求解得到b₀、b₁、b₂、…、b_m，并由以下公式求出回归方程的常数项b₀：

\(\left\{\begin{array}{c}l_{11} b_{1}+l_{12} b_{2}+\ldots+l_{1 m} b_{m}=l_{1 Y} \\\ldots \ldots \\l_{m 1} b_{1}+l_{m 2} b_{2}+\ldots+l_{m m}b_{m}=l_{m Y}\end{array}\right.\)

\(l_{ij}=\sum\left(X_{i}-\bar{X}_{i}\right)\left(X_{j}-\bar{X}_{j}\right)=\sum X_{i} X_{j}-\frac{\sum X_{i} \sum X_{j}}{n}\)

\(l_{iY}=\sum\left(X_{j}-\bar{X}_{j}\right)(\mathrm{Y}-\overline{\mathrm{Y}})=\sum X_{j} Y-\frac{\sum X_{j}\sum Y}{n}\)

\(i, j=1,2, \ldots, m\)

\(b_{0}=\bar{Y}-\left(b_{1} \bar{X}_{1}+b_{2}\bar{X}_{2}+\cdots+b_{m} \bar{X}_{m}\right)\)

其中，l_ij为自变量的离均差平方和(当i=j时)或两个自变量的离均差积和(当i≠j时)。l_iY为自变量X_j和应变量Y的离均差积和。

(二) 模型检验及评价

对回归模型及参数做假设检验，并对方程的拟合效果及各自变量的作用大小作出评价。详见下文。

三、多重线性回归中的统计推断及其评价

(一) 回归方程的假设检验及评价

由样本数据得到回归方程后，为了确定回归方程及引入的自变量是否有统计学意义，必须进一步做假设检验。方差分析法可以将回归方程中所有自变量X₁、X₂、…、X_m作为一个整体来检验它们与因变量Y之间是否具有线性关系，并对回归方程的预测或解释能力作出综合评价。在此基础上进一步对各变量的重要性作出评价。

1. 方差分析法

H₀：β ₁= β ₂= β ₃=…= β _m = 0

H₁：各β _j (j=1、2、…、m)不全为0

α = 0.05

将因变量Y的总变异分解成两部分，即：

\(\sum(\mathrm{Y}-\overline{\mathrm{Y}})^{2}=\sum(\mathrm{Y}-\widehat{\mathrm{Y}})^{2}+\sum(\widehat{\mathrm{Y}}-\overline{\mathrm{Y}})^{2}\)

其中\(\sum(\hat{Y}-\bar{Y})^{2}\)为回归平方和，\(\sum(Y-\hat{Y})^{2}\)

\(\mathrm{SS}_{\text {总 }}=\mathrm{SS}_{\text{残 }}+\mathrm{SS}_{\text {回 }}\)

回归平方和可用下式计算为：

\(\mathrm{SS}_{\text {回 }}=b_{1} l_{1 y}+b_{2} l_{2 r}+\cdots+b_{m} l_{m r}=\sum b_{j} l_{j Y}\)

用统计量F检验假设H₀是否成立

\(F=\frac{\mathrm{SS}_{\text {回 }} /m}{\mathrm{SS}_{\text {残 }}/(n-m-1)}=\frac{\mathrm{MS}_{\text{回 }}}{\mathrm{MS}_{\text {残 }}}\)

如果\(F \geq F_{(m, n-m-1)}\)，则在α水准上拒绝H₀，接受H₁，认为因变量Y与m个自变量X₁、X₂、…、X_m之间存在线性回归关系。

2. 决定系数R²

根据方差分析表中的结果，还可以得到多重线性回归的决定系数R²，其计算公式为

\(R^{2}=\frac{S S_{\text {回 }}}{S S_{\text {总 }}}=1-\frac{S S_{\text {残 }}}{S S_{\text {总 }}}\)

\(0 \leq R^{2} \leq 1\)，说明自变量X₁、X₂、…、X_m能够解释Y变化的百分比，其值越接近1，说明模型对数据的拟合程度越好。

3. 复相关系数

\(\mathrm{R}=\sqrt{R^{2}}\)称为复相关系数(multiple correlation coefficient)，可用来度量因变量Y与多个自变量间的线性相关程度，亦即观察值Y与估计值之间的相关程度。

如果只有一个自变量时，\(\mathrm{R}=|r|\)，r是简单相关系数。

(二) 各自变量的假设检验与评价

方差分析和决定系数是将所有自变量X₁、X₂、…、X_m作为一个整体来检验和说明它们与Y的相关程度及解释能力，并未指明方程中的每一个自变量对Y的影响如何，而在医学研究中往往更关心的是对各自变量的解释。对每一自变量的作用进行检验和衡量它们对Y的作用大小，可以采用下面一些方法。

1. 偏回归平方和

回归方程中某一自变量X_j的偏回归平方和(sum of squares for partial regression)，表示在模型中含有其他m-1个自变量的条件下该自变量对Y的回归贡献，相当于从回归方程中剔除X_j后所引起的回归平方和的减少量，或在m-1个自变量的基础上新增加X_j引起的回归平方和的增加量。这里，偏回归平方和用SS_回(X_j)表示，其值愈大说明相应的自变量愈重要。需要注意的是，m-1个自变量对Y的回归平方和由重新建立的新方程得到，而不是简单地在原方程基础上把b_jX_j剔除后算得。

利用某一自变量X_j的偏回归平方和检验H₀：β = 0, H₁：β ≠ 0是否成立，检验统计量为：

\(F=\frac{\mathrm{SS}_{\text {回 }}\left(X_{j}\right) /1}{\mathrm{SS}_{\text {残 }} /(n-m-1)}\)

如果\(F_{j} \geq F_{\alpha,(1, n-m-1)}\)，则在给定的α检验水准上拒绝H₁，认为Y与X_j有线性关系。同理，也可以对回归方程中的部分自变量做假设检验，如对回归方程中的X_j和X_j+1检验H₀：β_j=β_j+1= 0，检验统计量为

\(F=\frac{\mathrm{SS}_{\text {回 }}\left(X_{j},X_{j+1}\right) / 2}{\mathrm{SS}_{\text {残 }}/(n-m-1)}\)

各自变量的偏回归平方和可以通过拟合包含不同自变量的回归方程计算得到。

2. t检验法

t检验法是一种与偏回归平方和检验完全等价的方法，计算公式为

\(t=\frac{\mathrm{b}_{j}}{\mathrm{~S}_{\mathrm{b}_{j}}}\)

其中b_j为偏回归系数的估计值：S_bj是b_j的标准误，计算比较复杂，要应用矩阵运算获得。

原假设 H₀：β_j = 0，t_j服从自由度为v = n - m - 1的t分布。如果\(\left|t_{j}\right| \geq t_{\alpha / 2, n-m-1}\)，则在α检验水准上拒绝H₀，接受H₁，认为Y与X_j有线性回归关系。

3. 标准化回归系数

由于各自变量的测量单位不同，单从各偏回归系数的绝对值大小来分析难以得出正确的结论。若对数据标准化，即将原始数据减去相应变量的均数后再除以该变量的标准差：

\(X_{j}^{\prime}=\frac{\left(X_{j}-\bar{X}_{j}\right)}{S_{j}}\)

计算得到的回归方程称作标准化回归方程，相应的回归系数即为标准化回归系数。标准化回归方程的截距为0，标准化回归系数与一般回归方程的回归系数之间的关系为

\(b_{j}^{\prime}=b_{j} \sqrt{\frac{l_{j j}}{l_{YY}}}=b_{j}\left(\frac{S_{j}}{S_{Y}}\right)\)

式中\(b_{j}^{\prime}\)为标准化回归系数，S_j和S_Y分别为自变量X_j和应变量Y的标准差。标准化回归系数可以用来比较各个自变量X_j对Y的影响强度，通常在有统计学意义的前提下，标准化回归系数的绝对值愈大，说明相应自变量对Y的作用愈大。

(三)自变量选择方法

通常情况下，多重线性回归方程中并不是所有的自变量都是重要的。冗余的自变量引入方程可能降低模型的精度，因此选择有意义的自变量很重要。基本思路是尽可能将回归效果显著的自变量选入回归方程，而将作用不显著的自变量排除在外。

1. 全局择优法

全局择优法是对自变量各种不同组合所建立的回归方程进行比较，进而从全部组合中挑出一个“最优”的回归方程。下面给出两种具体的选择方法。

(1) 校正决定系数R²选择法

决定系数R²可以用来评价回归方程的优劣，但随着自变量个数的增加，R²将不断增大，若对两个具有不同个数自变量的回归方程进行比较时，不能简单地用R²作为评价回归方程的标准，还必须考虑方程所包含的自变量个数的影响。为此提出了校正的决定系数R²。其计算公式为

\(R_{c}^{2}=1-\left(1-R^{2}\right)\frac{n-1}{n-p-1}=1-\frac{M S_{\text {残 }}}{MS_{\text {总 }}}\)

式中n为样本含量，R²为包含\(p(p \leq m)\)个自变量的回归方程的决定系数。可以看出，当R²相同时，自变量个数越多，R²_c越小。所谓“最优”回归方程是指R²_c最大者。

(2)C_p选择法

C_p统计量定义为

\(C_{p}=\frac{\left(S S_{\text {残 }}\right)_{p}}{\left(MS_{\text {残 }}\right)_{m}}-[n-2(p+1)]\)

其中(SS_残)_p是由\(p(p \leq m)\)个自变量做回归得到的误差平方和，(MS_残)_m是从全部m个自变量的回归模型中得到的残差均方。可以证明，当由p个自变量拟合的方程理论上为最优时，C_p的期望值是p+1。因此应选择C_p最接近p+1的回归方程为最优方程。注意：当p = m时，必有C_m= m+1，这种情况不在选择之列，即应有p < m。

2. 逐步选择法

全局择优法建立的最优回归方程用于估计与预测的效果最好。但当自变量数目较大时，采用全局择优方法的计算量很大，如对于10个自变量，需要比较的方程个数增加到2¹⁰-1 = 1023个；另外，用全局择优法建立的回归方程，不能保证回归方程内的各自变量都有统计学意义。

逐步选择法可以克服这一不足，是实际应用中普遍使用的一类方法。而全局择优法则可以作为辅助评价模型优劣的指标。该法按照选入变量的顺序不同分为前进法(forward selection)、后退法(backward elimination)和逐步回归法(stepwise regression)。它们的共同特点是每一步只引入或剔除一个自变量X_j，决定其取舍则基于对偏回归平方和的F检验，即

\(F=\frac{S S_{\text{回 }}^{(l)}\left(X_{j}\right)}{\mathrm{SS}_{\text{残 }}(l) /(n-p-1)}\)

其中，p为进行到第l步时方程中自变量的个数，\(S S_{\text {回 }}^{(l)}\left(X_{j}\right)\)为第l步时X_j的偏回归平方和，\(\mathrm{SS}_{\text {残差 }}(l)\)为第l步时的残差平方和。对给定的检验水准α，若是方程外的自变量，当\(F \geq F_{\alpha,(n-p-1)}\)时可决定引入；若是方程内的自变量，当\(F<F_{\alpha,(n-p-1)}\)可决定剔除。

(1) 前进法

回归方程中的自变量从无到有、由少到多逐个引入回归方程。首先，将每个自变量X与因变量Y做直线回归，对回归平方和最大的自变量做F检验，若偏回归系数有统计学意义，则把该自变量引入方程。而后在余下的自变量中，考虑在进入方程的第一个自变量基础上，计算其他自变量的偏回归平方和，选取偏回归平方和最大的一个自变量做F检验以决定是否选入，如果有统计学意义则进入方程，然后再以同样的方式寻找第三个自变量，直到没有自变量可以引入为止。

前进法有一定的局限性，即后续变量的引入可能会使先进入方程的自变量变得无统计学意义。

(2) 后退法

后退法与前进法正好相反，它是先将全部自变量选入方程，然后逐步剔除无统计学意义的自变量。剔除自变量的方法是在方程中选一个偏回归平方和最小的变量，做F检验决定它是否剔除，若无统计学意义则将其剔除，然后对剩余的自变量建立新的回归方程。重复这一过程，直至方程中所有的自变量都不能剔除为止。

后退法的优点是考虑到了自变量的组合作用，选中的自变量数目一般会比前进法选中的多；其缺点是当自变量数目较多或某些自变量高度相关时，可能得不出正确的结果，前进法则可以自动去掉高度相关的自变量。

(3) 逐步回归法

逐步回归法是在前述两种方法的基础上，进行双向筛选的一种方法。该方法本质上是前进法，但每引入一个自变量进入方程后，要对方程中的每一个自变量做基于偏回归平方和的F检验，看是否需要剔除一些退化为“不显著”的自变量，以确保每次引入新变量之前方程中只包含有“显著”作用的自变量。这一双向筛选过程反复进行，直到既没有自变量需要引入方程，也没有自变量从方程中剔除为止，从而得到一个局部最优的回归方程。

对选入和剔除自变量的F检验，可以设置相同或不同的检验水准，一般对于小样本可把α值定为0.10或0.15，对大样本可以把α值设为0.05。α值定得越小表示选取自变量的标准越严，被选入的自变量个数相对也较少；反之，α值定得越大表示选取自变量的标准越宽，被选入的自变量个数也就相对较多。需要注意，选入自变量的检验水准α_入应小于或等于剔除自变量的检验水准α_出。

四、案例数据

某社区医师从本社区的糖尿病患者中随机抽取50名，收集了他们的性别(Gender)、经济水平(Income)、空腹胰岛素(Fasting insulin，mmol/L)、糖化血清蛋白(Glycosylated serum protein, GSP)和空腹血糖(FBS，mmol/L)，欲探究空腹血糖是否受到其他几项指标的影响。部分数据见图2。

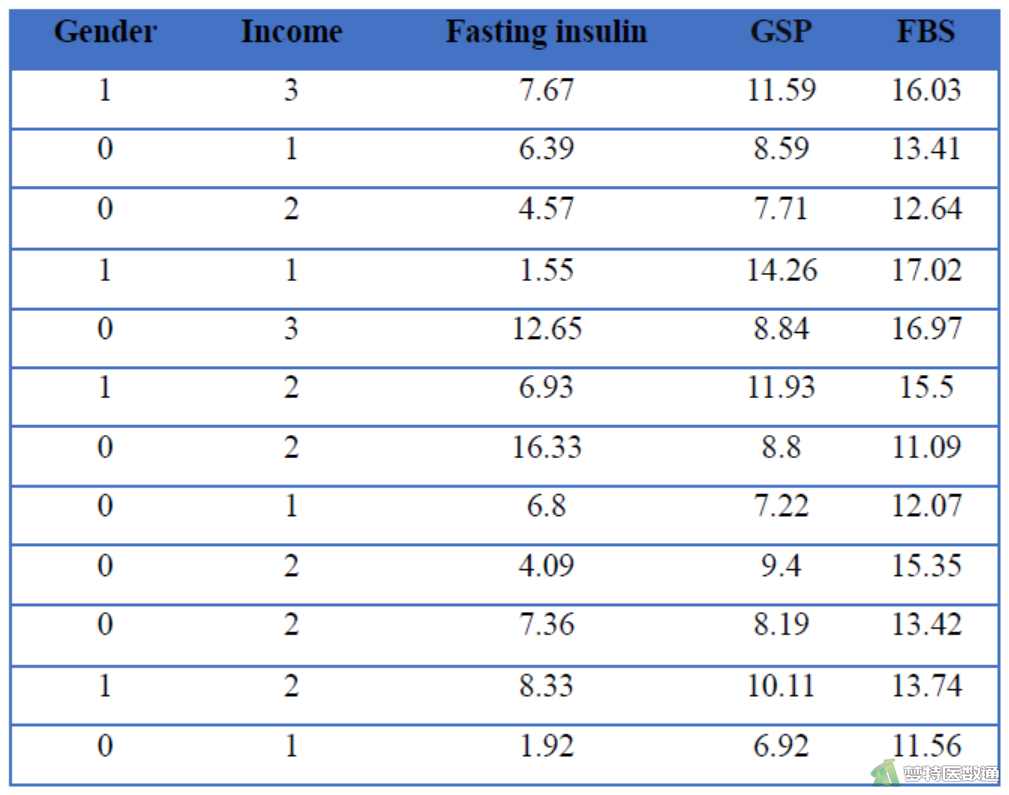
五、案例分析

(一) 回归方程的假设检验及评价

H₀：β ₁= β ₂= β ₃=…= β _m = 0，即性别、经济水平、空腹胰岛素和糖化血清蛋白与空腹血糖之间无线性关系。

H₁：各β _j (j=1、2、…、m)不全为0，即性别、经济水平、空腹胰岛素和糖化血清蛋白至少有一个与空腹血糖之间存在线性关系。

α = 0.05

此案例经过分层回归计算结果汇总在下文各图表。

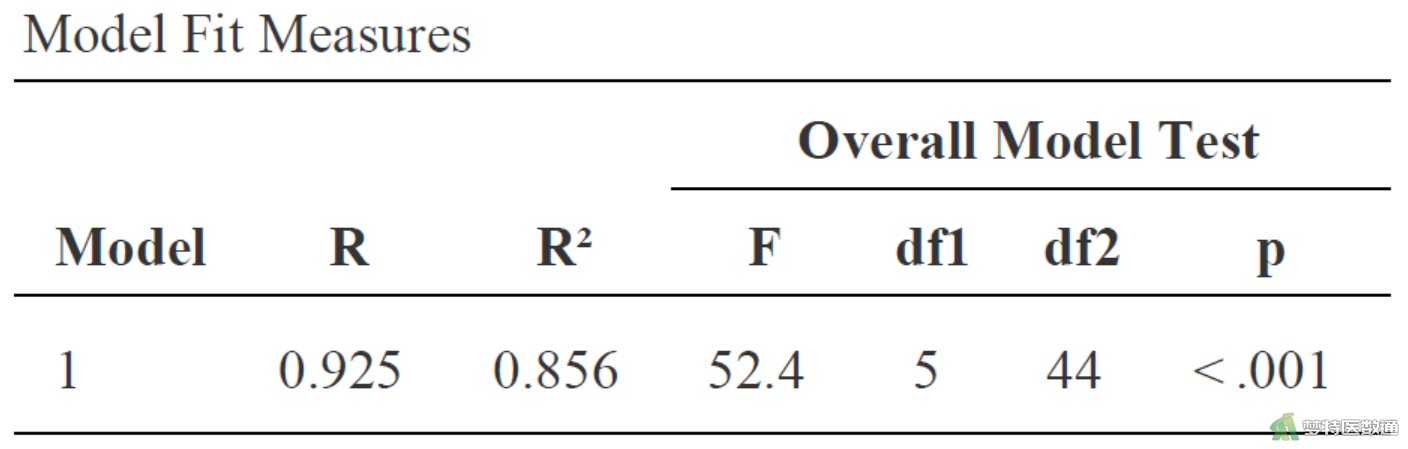
从图3可得该回归模型假设检验的P值<0.001，在α = 0.05水平拒绝H₀，接受H₁，说明性别、经济水平、空腹胰岛素和糖化血清蛋白至少有一个与空腹血糖之间存在线性关系。该模型的决定系数R² = 0.856，表示此例中性别、经济水平、空腹胰岛素和糖化血清蛋白可解释空腹血糖变异的85.6%。复相关系数R = 0.925即观察值Y与其估计值之间的相关程度为0.925。

(二) 各自变量的假设检验与评价

各自变量的假设检验结果如图4和图5。图4是各自变量的建设检验，可知，变量“性别”无统计学意义，可被移除模型。

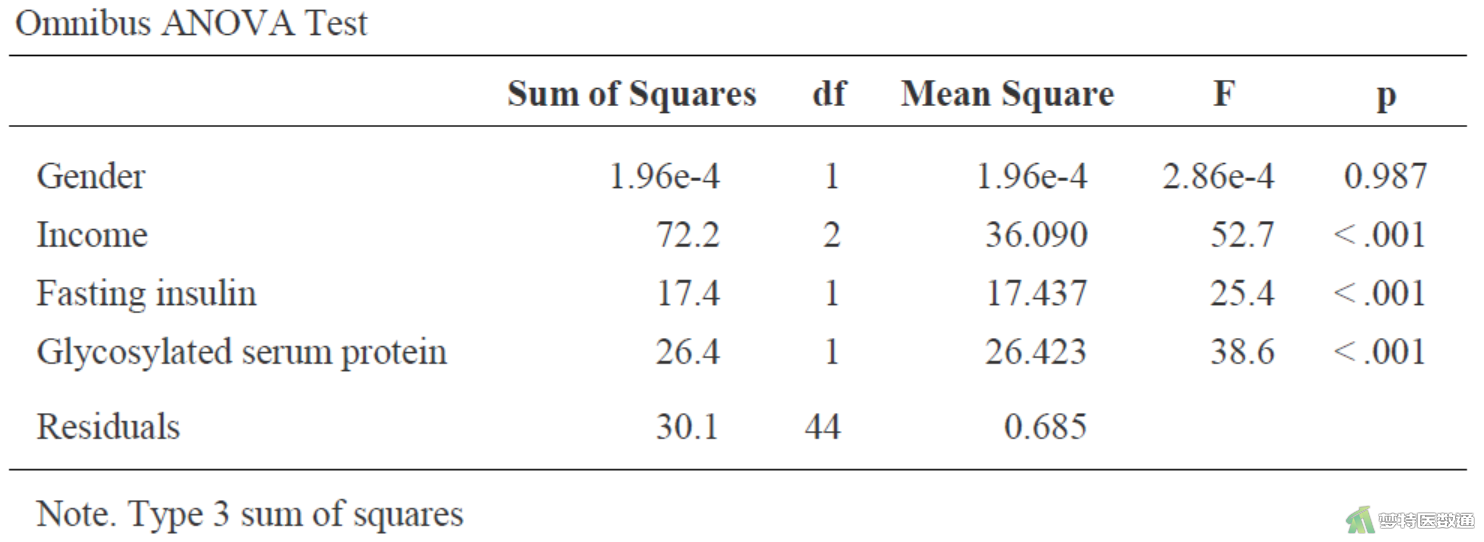
图5是各自变量的系数估计及假设检验结果，也可知，变量“性别”无统计学意义，可被移除模型。

可写出多重线性回归的估计方程为：

空腹血糖 = 9.562－0.005×性别(女性)－0.194×空腹胰岛素 + 0.502×糖化血清蛋白+ 0.815×(经济水平=中等收入) + 3.934×(经济水平=高收入)

(三) 模型优化

根据上述分析结果，去除“性别”自变量后再对其他变量进行多重线性回归分析，结果如下图表所示。

图6“Model Fit Measures (模型拟合评价)”结果中3个模型的复相关系数、决定系数和校正决定系数随着变量的增加而逐渐变大，AIC、BIC、RMSE均随着变量的增加而逐渐变小，表明随着变量的加入模型对因变量的解释能力增加。模型3的决定系数为0.856，校正决定系数为0.844，AIC为128.601，BIC为140.074，RMSE为0.777，表明模型整体拟合较好。“Overall Model Test (模型整体检验)”考察模型的整体显著性，可见3个模型均有统计学意义，表示3个模型中均至少有1个自变量具有统计学意义。

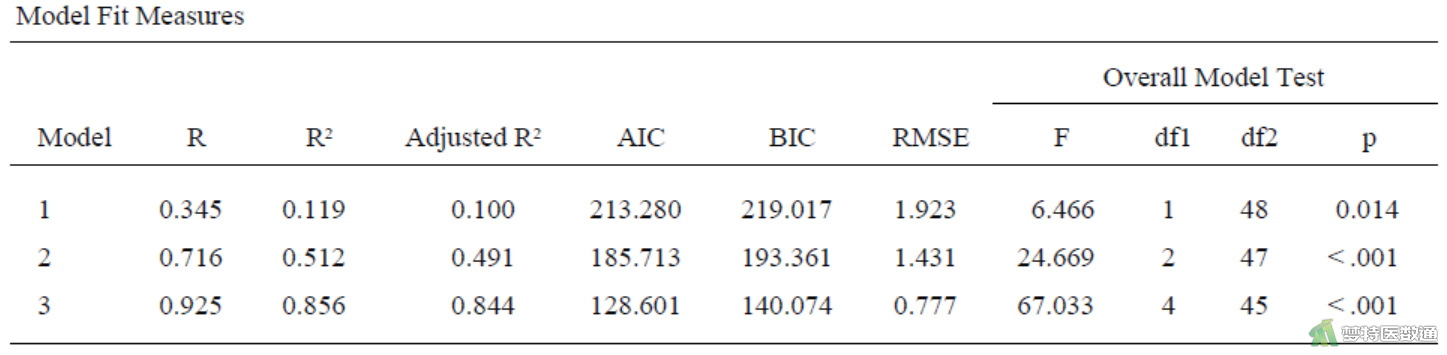
图7“Omnibus ANOVA Tests (整体方差分析)”中所有自变量均有统计学意义。

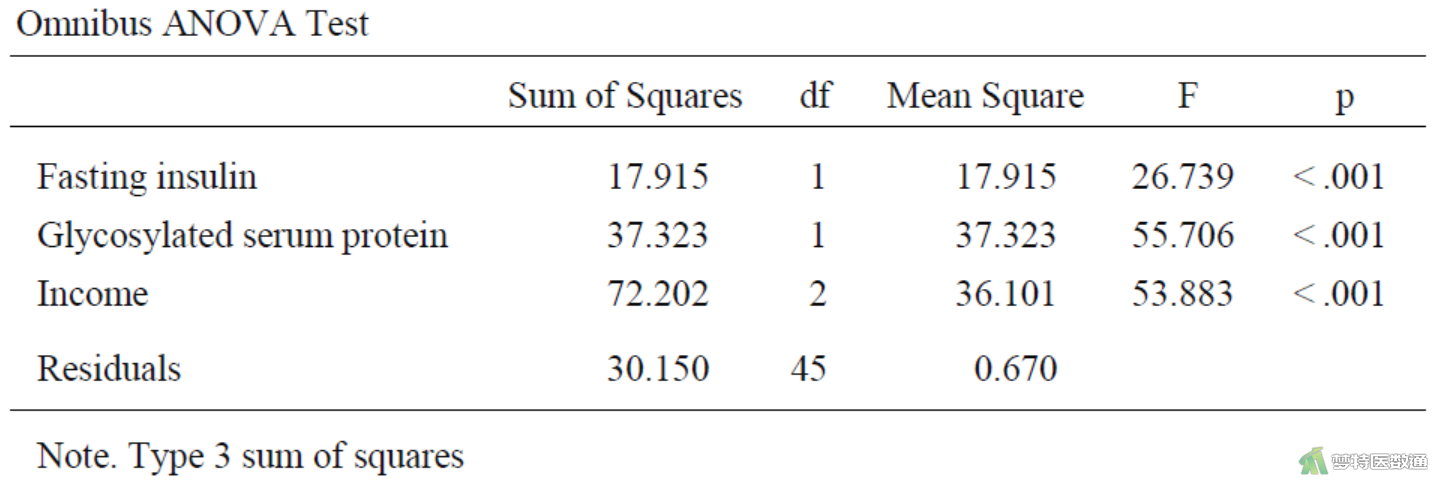
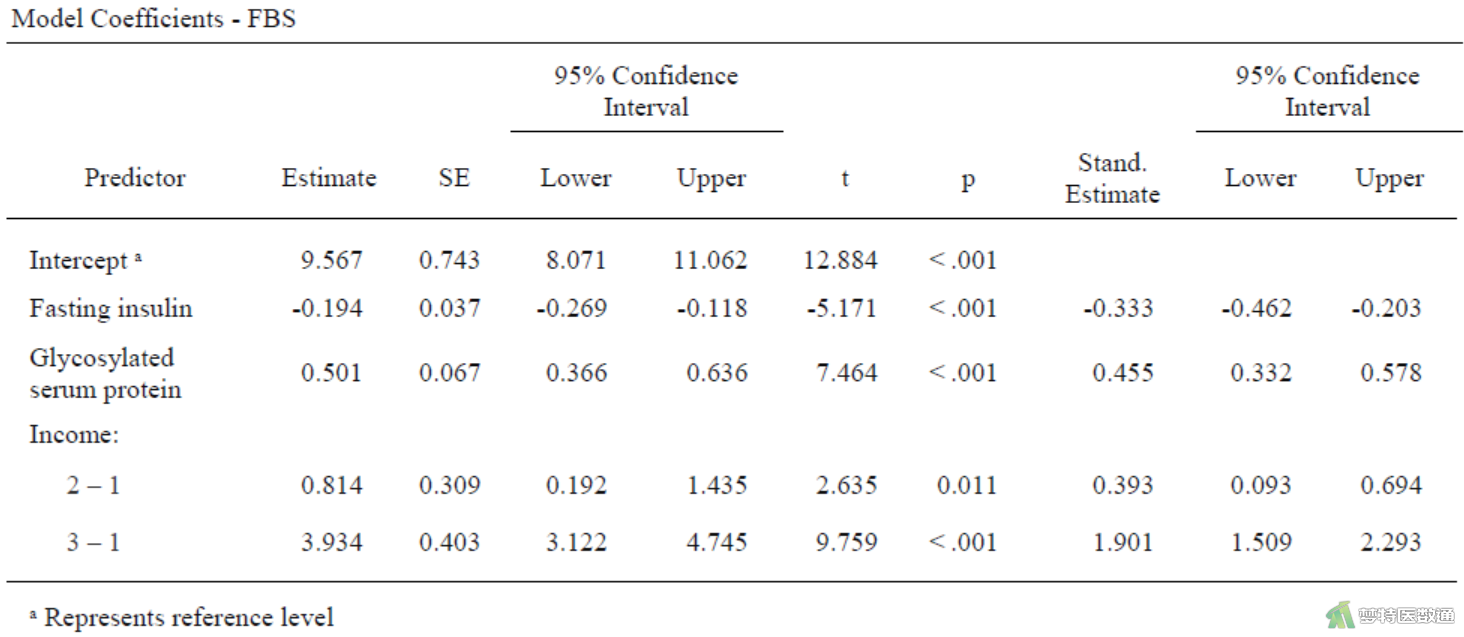
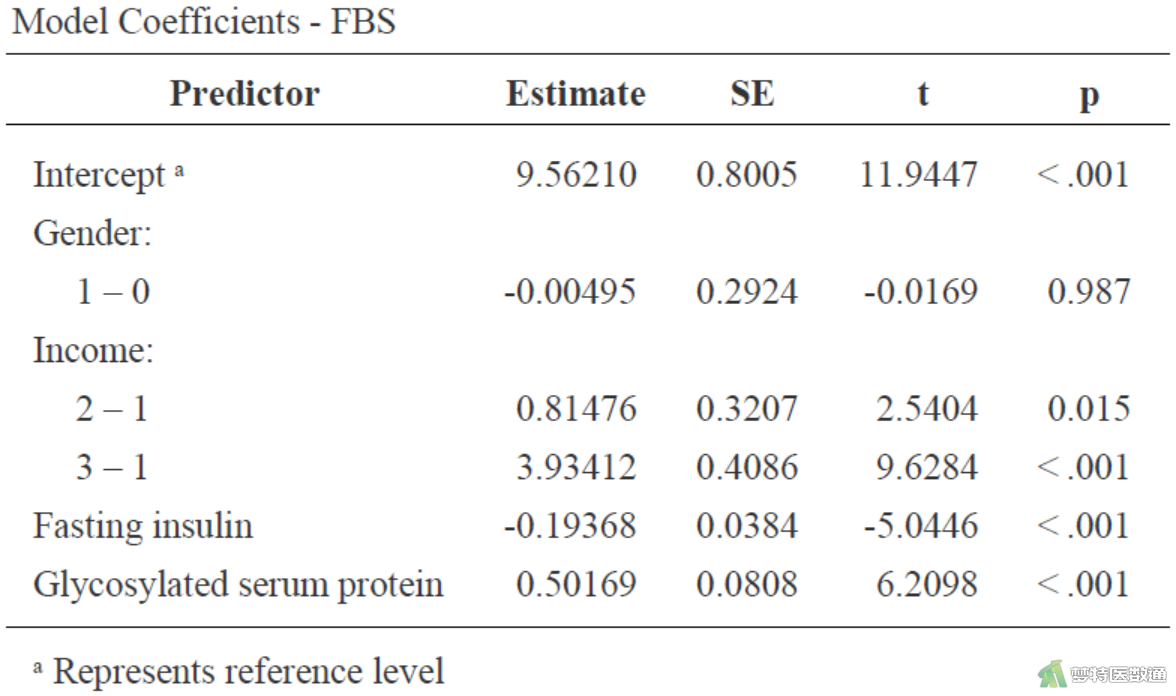
图8中回归模型的截距为9.567，表示纳入的各自变量取值均为0时，因变量的平均估计值，并无实际专业意义。变量“空腹胰岛素”的非标准化系数(即斜率)为-0.194 (95%CI：-0.269~-0.118，P<0.001)，表示“空腹胰岛素”每增加1mmol/L，空腹血糖减少0.194 mmol/L；变量“糖化血清蛋白”的非标准化系数(即斜率)为0.501 (95%CI：0.366~0.636，P<0.001)，表示“糖化血清蛋白”每增加1%，空腹血糖增加0.501 mmol/L。相比“低收入”人群而言，“中等收入”人群的非标准化系数为0.814 (95%CI：0.192~1.435，P=0.011)，表示“中等收入”人群比“低收入”人群空腹血糖高0.814 mmol/L；相比“低收入”人群而言，“高收入”人群的非标准化系数为3.934 (95%CI：3.122~4.745，P<0.001)，表示“高收入”人群比“低收入”人群空腹血糖高3.934 mmol/L。

最终，确定模型为：

空腹血糖 = 9.567 - 0.194×空腹胰岛素 + 0.501×糖化血清蛋白+ 0.814×(经济水平=中等收入) + 3.934×(经济水平=高收入)