在前面文章中介绍了简单线性回归分析 (Simple Linear Regression Analysis)——理论,本文将实例演示在MedCalc软件中实现简单线性回归分析的操作步骤。
关键词:MedCalc; 简单线性回归; 直线回归; 残差齐性检验; 残差正态检验; 哑变量设置
一、案例介绍
研究健康成年人的体重和双肾脏总体积(ml)的关系,测得24名健康成年人的体重wt (kg)与双肾脏总体积volume (ml),拟探讨健康成年人的体重与双肾总体积是否有关,并希望通过健康成年人的体重预测双肾总体积。部分数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析
本案例的分析目的是通过判断两个计量资料之间的关系,同时使用其中一个变量预测另一个变量,计算其中一个变量对另一个变量变异的解释程度。针对这种情况,可以使用简单线性回归分析。但需要满足6个条件:
条件1:因变量为连续变量。本研究中,健康成年人的体重为连续变量,该条件满足。
条件2:若自变量是连续变量,则与因变量之间存在线性关系。该条件需要通过软件分析后判断。
条件3:各观测值之间相互独立,即残差之间不存在自相关。通过研究设计和数据收集的过程分析,可判断本案例中观测值之间不存在互相影响的情况。该条件满足。
条件4:自变量不存在显著的异常值,该条件需要通过软件分析后判断。
条件5:残差符合正态(或近似正态)分布,该条件需要通过软件分析后判断。
条件6:残差方差齐。该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 数据准备
1. 变量标签设置
点击左侧“变量”,出现“变量”对话框,在此处选中需要进行标签设置的变量后,点击右侧“属性”(图2)。
打开“变量属性”对话框,先设置volume的标签(图3),再设置wt的标签。
2. 计算残差值
在回归分析中,残差是指因变量预测值和观测值间的差值。异常值检测、正态性检验和方差齐性检验均可通过残差分析完成。
(1) 软件操作
点击“统计”—“回归”—“回归”(图4)。

在“回归”主对话框中设置如下参数(图5),并点击确定
①变量Y:即纵轴变量。本例选择volume。
②变量X:即横轴变量。本例选择wt。
③重量:即权重,进行加权最小二乘回归时需选择一个包含每个观测值相对权重的变量。本例默认不进行选择。
④筛选条件:即设定统计分析的个案子组。本例未选择任何变量。
⑤回归方程:默认选择“在方程中包含常量”,为普通最小二乘回归的推荐选项。此外包括5种不同的回归方程供选择:“y=a+bx”表示直线方程;“y=a+blog(x)”表示对数曲线方程;“log(y)=a+bx”表示指数曲线方程;“log(y)=a+blog(x)”表示几何曲线方程;“y=a+bx+cx2”表示二次回归方程。本例选择“y=a+bx”。 ⑥残差:选择进行正态分布检验的方法,主要包括“Shapiro-Wilk检验(常用于3≤n≤50的小样本资料)”“Shapiro-Francia检验(常用于5≤n≤5000的资料)”“D’Agostino-Pearson检验(常用于50≤n≤1000的资料)”“、Kolmogorov-Smirnov检验(常用于n>50的资料)”“卡方检验(适用于分箱资料)”。本例选择“Shapiro-Wilk检验”。

(2) 结果解读
模型拟合的各项参数见图6,将在“统计描述和推断”部分详细说明,此处点击“保留残差”,在“保存残差”对话框(图7)中,勾选“标准化”后,在数据表最后新增了一列“REGR_Resid1”。

(二) 适用条件判断
1. 条件2判断(线性关系判断)
(1) 软件操作
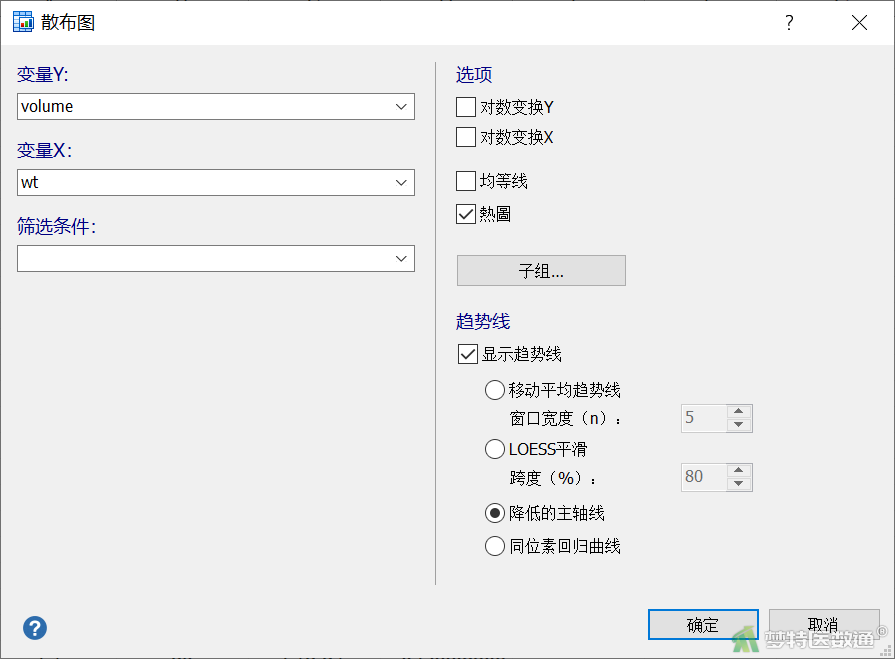
点击“统计”—“相关”—“散布图”(图8)
在“散布图”主对话框中设置如下参数(图9),并点击确定
①变量Y:即纵轴变量。本例选择volume。
②变量X:即横轴变量。本例选择wt。
③筛选条件:即设定统计分析的个案子组。本例未选择任何变量。
④选项:“对数变换Y”表示将变量Y进行对数变换,“对数变换X”表示将变量X进行对数变换,“均等线”表示在图形中绘制均等线(y=x),“热图”表示在图中绘制热图。本例选择“热图”。 ⑤趋势线:可选择绘制以下类型趋势线:“移动平均趋势线”可显示平滑资料的波动并将趋势显示得更明显,窗口宽度即为指定数量的数据点,移动平均趋势线将根据这些数据点的平均值作为趋势线的点;“LOESS平滑”即为局部回归平滑趋势线,跨度为用于每个局部拟合线的数据点数占所有数据点的比例,跨度值最大时为平滑趋势线;“降低的主轴线”显示压轴回归线,可同时考虑因变量(Y轴)和自变量(X轴)的测量误差;“同位素回归曲线”此处不适用。本例选择“降低的主轴线”。
(2) 结果解读
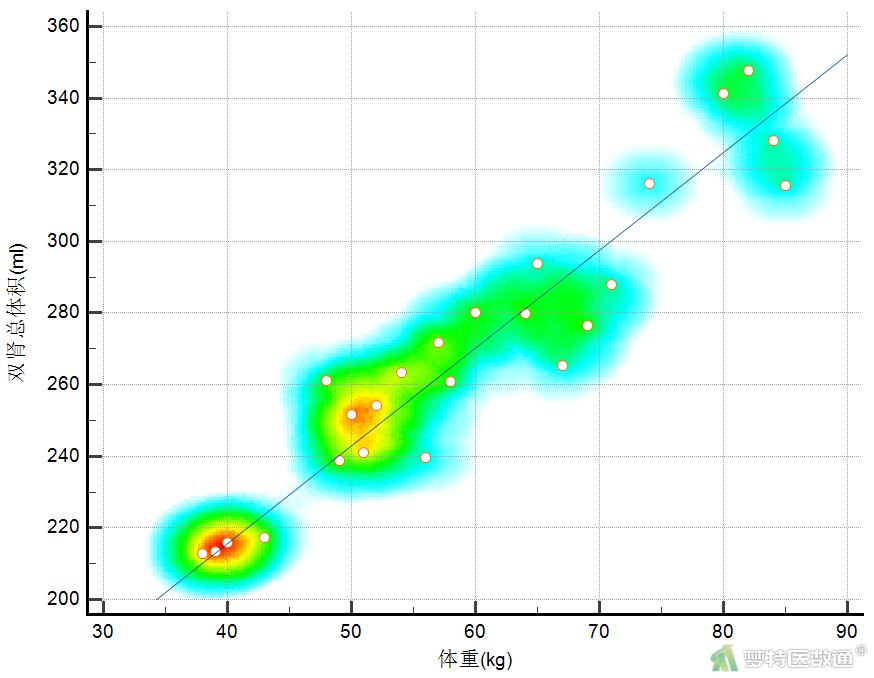
热图(图10)显示,散点大致呈一条直线,说明两变量存在线性关系。该条件满足。
2. 条件4判断(异常值判断)
(1) 软件操作
检测自变量“REGR_Resid1”的异常值情况。
点击“统计”—“异常值检测”(图11)

在“异常值检测”主对话框中设置如下参数(图12),并点击确定
①变量:即包含分析资料的变量。本例选择REGR_Resid1。
②筛选条件:即设定统计分析的个案子组。本例未选择任何变量。
③异常值检测方法:包括以下类型“Grubbs-左侧”表示进行只检查最小值的Grubbs检验;“Grubbs-右侧”表示进行只检查最大值的Grubbs检验;“Grubbs-两侧”表示进行检查两侧极端值的Grubbs检验;“生成的ESD检验”即广义ESD检验,可一次检测多个异常值,可设置最多可检测的异常值数,默认为10;“Turkey”即Turkey检验,可检出两侧的多个异常值。本例选择了后3种检测方法。
④选项:“Alpha级”表示进行Grubbs检验和ESD检验时的检验水准,本例选择“0.05”;“对数变换”表示当资料不服从正态分布时可对变量进行对数变换后再分析,本例不勾选;“检验正态分布”选择进行正态分布检验的方法,本例选择“Shapiro-Wilk检验”。

(2) 结果解读
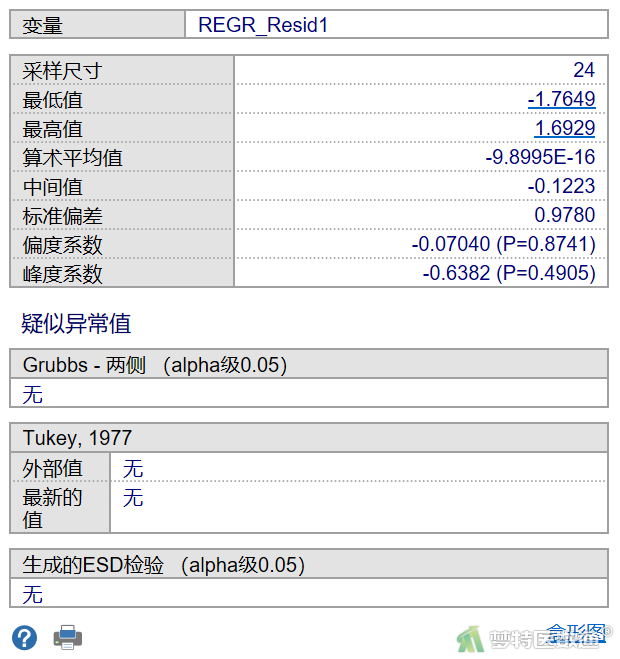
残差检验结果见图13,列出了残差的最小值和最大值,均在-3~3之间,提示无异常。Grubbs和Turkey检验也未提示任何异常值。满足条件4。
3. 条件5判断(残差正态性检验)
(1) 软件操作
检测残差变量“REGR_Resid1”的正态性情况。
点击“统计”—“分布图”—“正态图”(图14)
在“正态图”主对话框中设置如下参数(图15),并点击确定
①变量:即包含分析资料的变量。本例选择REGR_Resid1。
②筛选条件:即设定统计分析的个案子组。本例未选择任何变量。
③选项-Q-Q图:选择后将绘制Q-Q图,可以粗略评价资料是否服从正态分布。
④选项-检验正态分布:选择进行正态分布检验的方法,主要包括主要包括“Shapiro-Wilk检验(常用于3≤n≤50的小样本资料)”“Shapiro-Francia检验(常用于5≤n≤5000的资料)”“D’Agostino-Pearson检验(常用于50≤n≤1000的资料)”“、Kolmogorov-Smirnov检验(常用于n>50的资料)”“卡方检验(适用于分箱资料)”。本例选择“Shapiro-Wilk检验”。

(2) 结果解读

残差变量“REGR_Resid1”的Q-Q图见图16,可见散点基本围绕对角线分布,提示服从正态分布。满足条件5。
4. 条件6判断(残差的方差齐性检验)
(1) 软件操作
点击“统计”—“回归”—“散布图和回归线”(图17)

在“散布图和回归线”主对话框中设置如下参数(图18),点击“确定”
①变量Y:即纵轴变量。本例选择volume。
②变量X:即横轴变量。本例选择wt。
③重量:即权重,进行加权最小二乘回归时需选择一个包含每个观测值相对权重的变量。本例默认不进行选择。
④筛选条件:即设定统计分析的个案子组。本例未选择任何变量。
⑤回归方程:默认选择“在方程中包含常量”,为普通最小二乘回归的推荐选项。此外包括5种不同的回归方程供选择:“y=a+bx”表示直线方程;“y=a+blog(x)”表示对数曲线方程;“log(y)=a+bx”表示指数曲线方程;“log(y)=a+blog(x)”表示几何曲线方程;“y=a+bx+cx2”表示二次回归方程。本例选择“y=a+bx”。
⑥选项:选择回归线绘制的方式,包括“95%置信”(绘制总体回归线的95%置信区间)、“95%预测”(绘制回归曲线的95%预测区间,比95%置信区间宽)、“画均等线y=x”和“热图”。本例选择“95%置信”。
⑦残差:选择该选项将绘制残差图,可直观评价所选模型的拟合优度。

(2) 结果解读
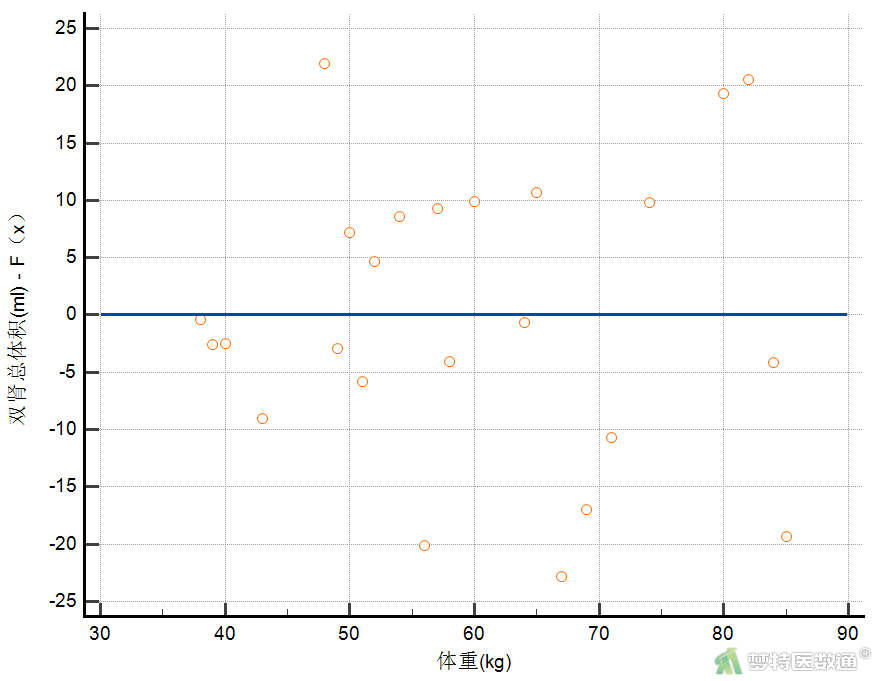
结果见图19,预测值和对应的残差分布较为均匀,并未出现特殊的分布形式(如漏斗或者扇形),提示残差的方差齐,满足条件6。残差分布图,也可以通过回归分析保存标准化预测值(图6、图7),然后以标准化预测值为横坐标,以标准化残差为纵坐标绘制散点图,得到的图形与图19一样(感兴趣的读者可自行操作)。
(三) 统计描述及推断
1. 软件操作
经过上述操作,已经输出了简单线性回归模型的结果。
2. 结果解读
(1) 模型拟合程度
回归分析结果(图6)中列出了模型的各项参数。决定系数R2(R-square)=0.8961,提示自变量(体重)可以解释89.61%的因变量的变异(双肾总体积)。整体模型检验结果显示F=189.8371,P<0.0001,提示模型有意义。如果P>0.05,则说明回归模型无统计学意义。
(2) 回归系数解释
回归分析结果(图6)中也列出了截距和自变量的回归系数及回归系数95%CI、t值及P值。可知,回归模型的截距为115.1194,表示自变量取值为0时,因变量的取值,并无实际专业意义。变量“wt”的非标准化系数(即斜率)为2.5849 (95%CI:2.1958~2.9740),表示体重每增加1 kg,双肾体积增加2.5849 ml。据此可以写出本案例的回归方程为:
Volume =115.1194+2.5849×wt
根据此方程可以计算合理范围内体重对应的双肾总体积。
四、结论
本研究采用简单线性回归模型通过健康成年人的体重预测双肾总体积。通过绘制散点图,提示两变量之间存在线性关系;通过专业判断提示数据之前相互独立;通过对残差进行Grubbs和Turkey检验,提示数据不存在需要处理的异常值;通过绘制残差Q-Q图,提示残差符合正态分布;通过绘制残差图,提示残差方差齐。本研究数据满足线性回归分析条件。
线性回归分析方程为volume = 115.1194 + 2.5849×wt,回归模型具有统计学意义,F=189.8371,P<0.0001;自变量(体重)可以解释89.61%的因变量(双肾总体积)的变异,影响程度较高,即体重每增加1 kg,双肾总体积增加2.5849 (95%CI 2.1958~2.9740) ml。
五、分析小技巧
分析中得到的回归截距为自变量取值为0时因变量对应的值。本研究中,回归截距为当体重为0时,研究对象的平均双肾体积115.1194 ml。这显然不符合客观实际,因此无论截距的统计检验结果是否有统计学意义,在进行简单线性回归时一般都无需关注这个指标,需要关注的是斜率。
在进行回归分析时,要注意避免对数据的过度挖掘,不能将回归模型分析的结果随意延伸到自变量取值范围以外的数值。也不能随意将模型分析结果延伸到因果关系。