Cox比例风险回归模型(Cox Proportional Hazard Regression Model)——MedCalc软件实现

关键词：MedCalc; Cox等比例回归; Cox回归; 生存分析; 等比例风险

一、案例介绍

某肿瘤研究所收集了200例肺癌患者的生存数据，现欲探究患者的性别、年龄、卡氏评分与生存结局的关系，部分数据见表1。其中，ID是肺癌患者的编号，time表示患者的生存时间(天)，status表示生存状态(0=删失，1=死亡)，age表示患者年龄(岁)，sex表示患者性别(1=男，2=女)，ph.karno表示卡氏评分。本案例数据可从“附件下载”处下载。

二、案例分析

本案例的目的是探究肺癌患者的性别、年龄和卡氏评分与生存结局的关系，可以采用Cox比例风险回归模型进行分析，但需要满足5个条件：

条件1：因变量是含有时间信息的二分类变量。本案例中因变量是包含生存时间的二分类资料，time是生存时间(天)；status是生存结局。该条件满足。

条件2：各观测值之间相互独立，无互相干扰。由数据和研究设计可知，该条件满足。

条件3：一般要求例数较少类(如删失组)的样本量为自变量个数的10~20倍(EPV原则)，且经验上两组的人数最好＞30例，参照水平组不应少于30或50例。该条件需要软件分析来判断。

条件4：自变量之间无严重多重共线性。该条件需要软件分析来判断。

条件5：满足等比例风险(proportional hazards，PH)假设，该条件需要软件分析来判断。

三、软件操作及结果结果

(一) 导入数据

将表1内容导入MedCalc中。部分数据见图1。

(二) 适用条件判断

1. 条件3判断

对结局变量“status”进行汇总统计。

(1) 软件操作

选择“统计”—“汇总统计”。在“汇总统计”对话框中，“变量”选择status，见图2。点击“更多选项”，打开“汇总统计表选项”对话框，“识别子组的类别变量”选择“status”，见图3。

(2) 结果解读

汇总结果见图4。从图中可看出，status=0的子组样本量是42。按照EPV为10~20的原则可满足多因素模型纳入3个变量的需求。对于“参照水平组不应少于30或50例的条件”，本案例不做硬性要求。因此，满足条件3。

2. 条件4判断

共线性诊断

(1) 软件操作

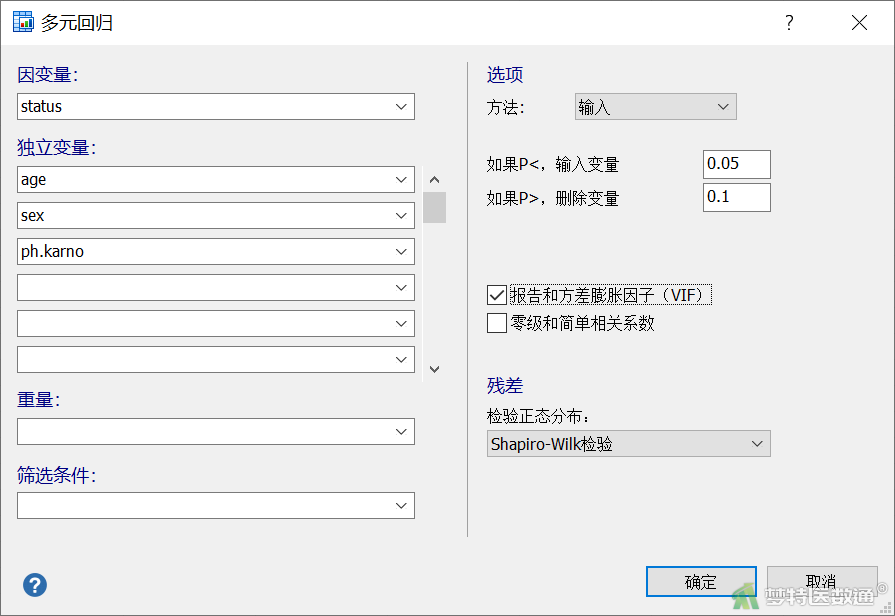
选择“统计”—“回归”—“多元回归”。在“多元回归”对话框中，“因变量”选择status，“独立变量”选择age、sex、ph.karno, 勾选“报告和方差膨胀因子(VIF)”，见图5。

(2) 结果解读

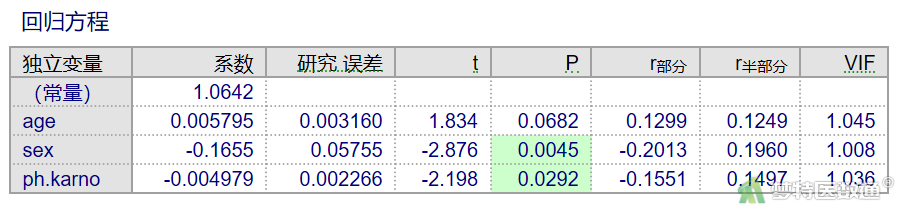
VIF=1，认为自变量间不存在共线性；1＜VIF≤5，认为自变量间存在较低的共线性；5＜VIF≤10，认为自变量间存在较高的共线性；VIF＞10，则提示有严重共线性存在。回归方程结果见图6，可知各变量VIF均在1左右，提示自变量之间不存在多重共线性。满足条件4。

3. 条件5判断

PH假设指自变量对生存率[风险比值h(t)/h0(t)]的影响不会随时间的变化而变化。在MedCalc中考察连续性变量的PH条件比较麻烦，此处可将连续性变量转换为分类变量进行考察。本案例中主要在于演示操作过程，因此将年龄(age)和卡氏评分(ph.karno)转换为二分类变量后进行PH判断。但这种方法的缺陷是，分类变量满足PH假设，不代表连续性变量满足PH假设，因此如果使用分类变量进行的PH判断，后续分析也需要使用分类变量进行Cox回归分析。

(1) 软件操作

对连续性变量age创建中位数分组，分为2组，对应的新变量命名为age_Median。

选择“工具”—“创建组”—“分位数”。在“创建分位数组”对话框(图7)中，“标题”命名为“age_Median”，“带案例标识的变量”选择“age”，“组变量”输入“2”。

重复上述步骤，对ph.karno也进行中位数分组，对应的新变量为ph.karno_Median。

参考(单样本生存资料的Kaplan-Meier法——MedCalc软件实现)绘制各因素的Kaplan-Meier生存曲线，对连续变量根据中位数分成大小两类，绘制生存曲线。性别、年龄分组及卡氏评分分组的生存曲线图结果见图8-1~8-3。

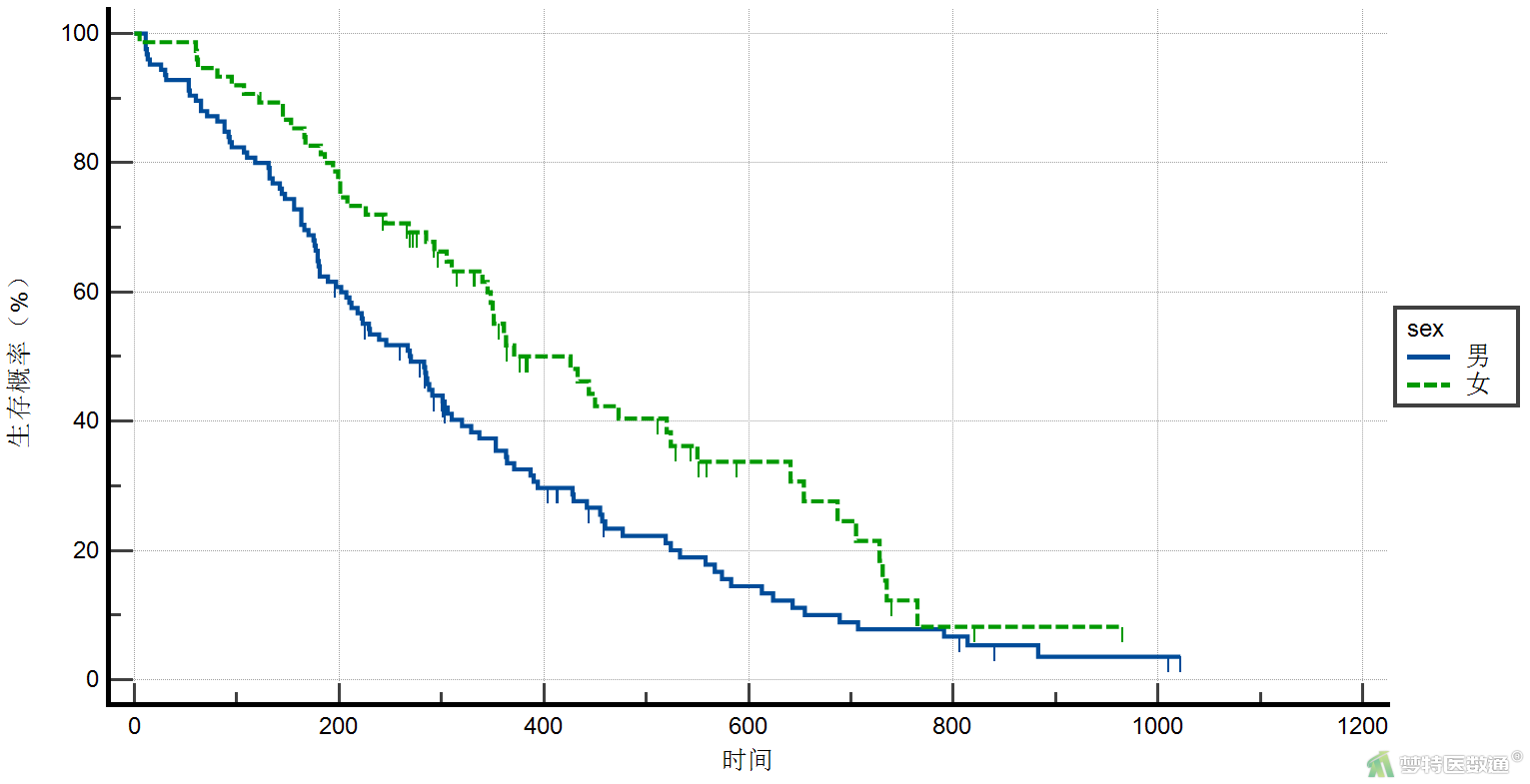
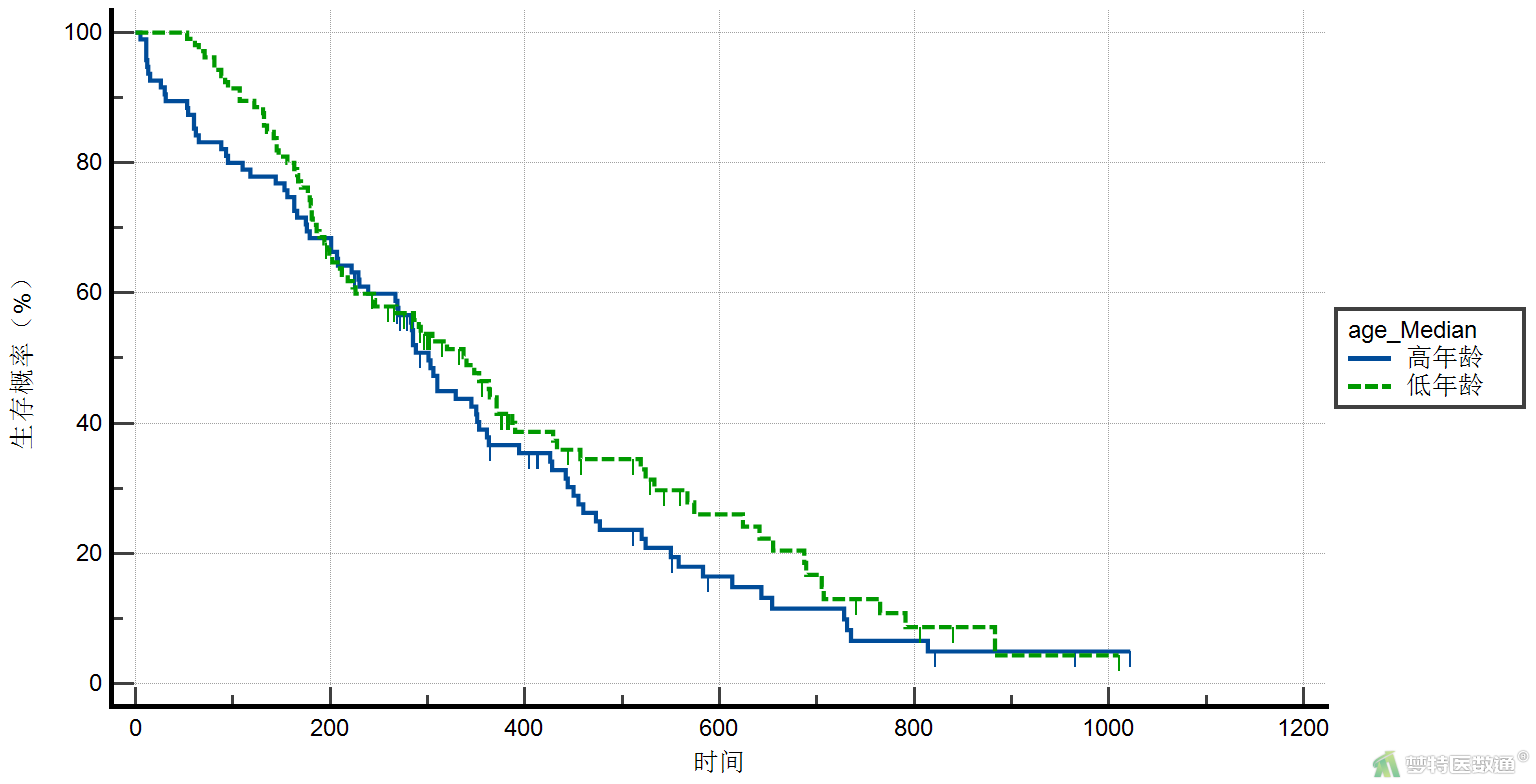
(2) 结果解读

从图8-1~图8-3可见，性别、年龄分组及卡氏评分分组的生存曲线不交叉，说明PH假设成立。满足条件5。

2. 单因素分析

(1) 软件操作

① 选择“统计”—“生存分析”— “Cox比例风险回归”(图9)。

② 打开“Cox比例风险回归”对话框(图10)，各个选项含义如下。

生存时间：选择包含生存时间的变量。本例为Time。

终点：选择包含结局编码的变量，默认“1”表示完全数据(即死亡组)，“0”表示删失数据，也可点击“定义状态”，在“定义状态”子对话框中，设定其他编码表示完全数据和删失数据。本例为Status，状态是默认值。

预测变量：用于预测生存时间的变量(即自变量)。Cox比例风险回归假设协变量随着时间变化的影响是恒定的。因此，终点与协变量应存在线性关系。对于严重偏态的协变量，可能需要进行对数变换以减少对极端值的影响。如需对协变量进行对数变换，则可输入“LOG(变量名)”。首先分析性别(sex)变量的生存情况，选择sex。

筛选条件：本案例不选择任何变量。

选项:本例默认选项。

[方法]选择协变量引入模型的方式。

 【输入】即全部进入法，一步将所有变量引入模型。

 【向前】即向前选择法，逐个引入有统计学显著性的变量。

 【向后】即后向剔除法，首先将所有变量引入模型，然后逐个剔除没有统计学显著性的变量。

 【逐步】即逐步法，逐个引入有统计学显著性的变量，当引入一个变量后，检查并剔除模型中没有统计学显著性的变量。此时为单因素分析，只有一个自变量，因此选择“输入”。

[如果P<，输入变量]：如果变量相关的显著性水平<P,则引入该变量。

[如果P>，删除变量]：如果变量相关的显著性水平>P,则剔除该变量。

[分类]：打开类别变量对话框。选择“选择类别变量”选择sex，并选择“将第一个类别作为参考类别”，点击“确定”。见图11。

图表选项

[图表]：本例选择“生存概率(%)”。

【生存概率(%)】绘制生存曲线，为下降曲线。

【100-生存概率(%)】绘制100-生存概率图，即累积死亡曲线，为上升曲线。

[图表子组]：选择一个自变量，将显示该自变量(预测变量)所有分类对应的不同生存曲线(最多不能超过8个分类)，如果不选择自变量或所选变量不在回归模型中，则绘制所有变量平均值的生存曲线。本例默认选项。

重复上述步骤，得到年龄分组和卡氏评分分组的单因素分析结果。

(2) 结果解读

单因素Cox比例风险模型分析显示(图12-1~图12-3)，性别和卡氏评分分组与生存结局之间存在统计学关联(P<0.05)，年龄分组与生存结局之间不存在统计学关联(P=0.2422)。

2. 多因素分析

将单因素Cox比例风险模型分析中有统计学关联的变量(性别和卡氏评分分组)纳入到多因素Cox比例风险模型，也可以将3个变量同时纳入多因素分析模型，自变量的选择可参考二分类logistic回归分析(Binomial Logistic Regression Analysis)——SPSS软件实现。

(1) 软件操作

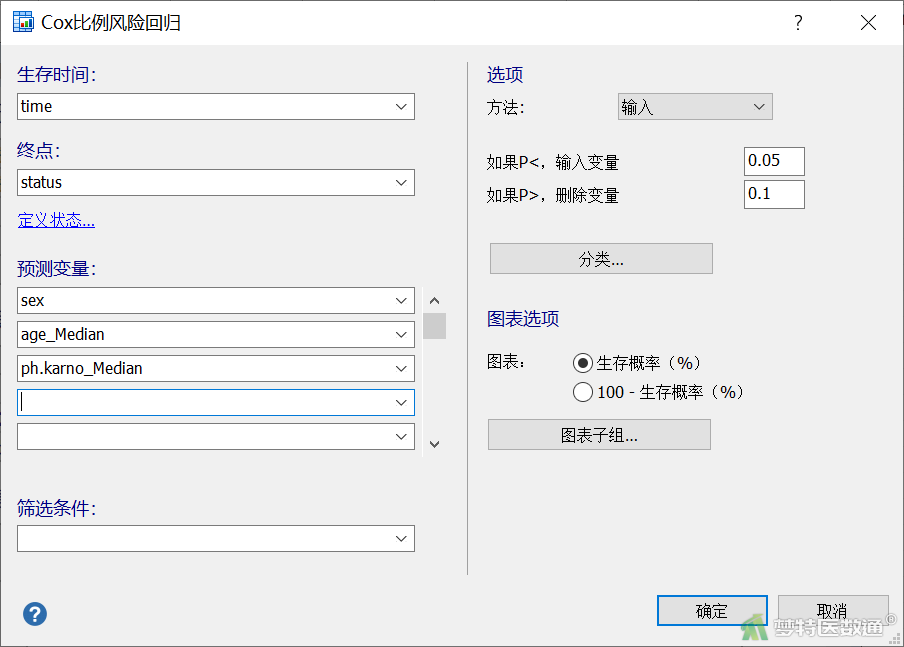
参照上述单因素Cox回归分析步骤，将3个变量同时纳入模型进行多因素Cox回归分析，“选项”中选择“逐步”。见图13。

(2) 统计描述与推断

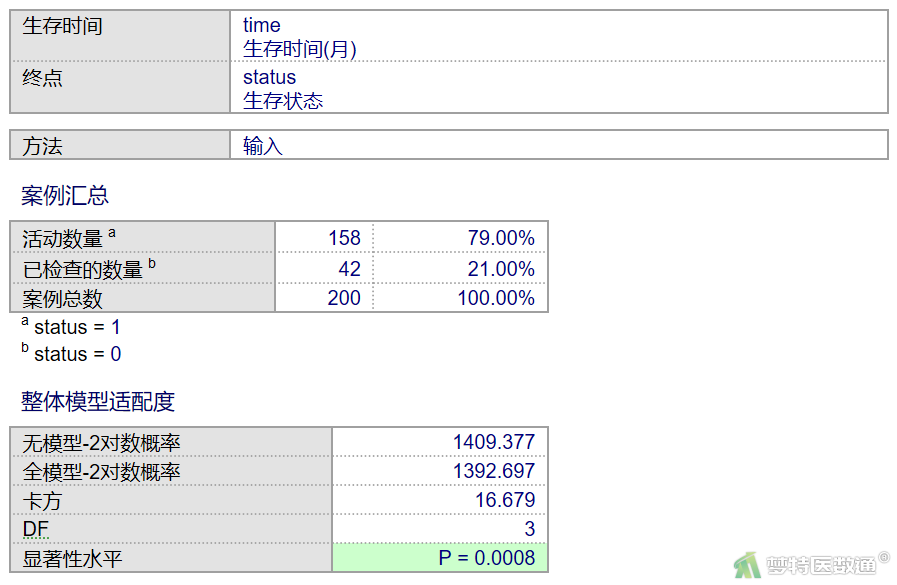
整体模型拟合优度：似然比检验是对模型回归系数整体的假设检验。空模型的-2对数似然，即-2lnL₀，L₀为只包含截距的模型(空模型)的最大似然。全模型的-2对数似然，即-2lnL，L为模型中包含所有协变量的最大似然。两个最大似然值的差值为用于测量协变量影响结局或因变量效果的χ²统计量。本例χ²=16.679，P=0.0008，即按α=0.05水准，拒绝H₀，接受H₁，全模型有统计学意义，即模型中的所有自变量整体来看与\ln \frac{H(t)}{H_{0}(t)}之间存在线性关系，表明模型中的自变量有助于预测结局，见图14。

变量系数：可见经过多因素分析后，性别和卡氏评分分组与生存结局之间存在统计学关联(P<0.05)，年龄分组与生存结局之间不存在统计学关联(P=0.3198)。对于肺癌患者，女性肺癌患者死亡风险比男性低39.82% (HR=0.6018, 95%CI 0.4304~0.8415)；卡氏评分高组的肺癌患者死亡风险比卡氏评分低组要低33.33% (HR=0.6667, 95%CI 0.4841~0.9183)，见图15。

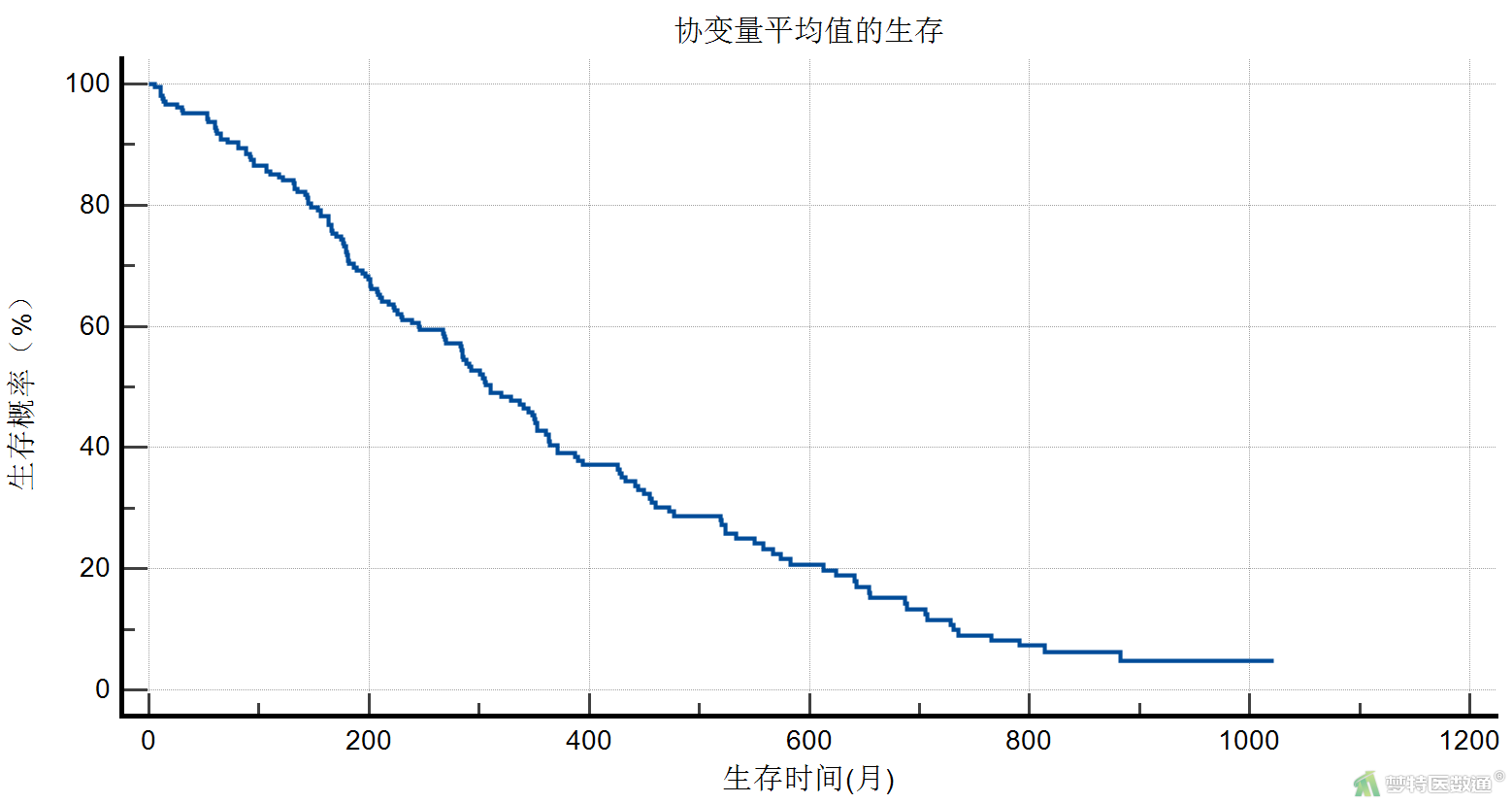
从协变量平均值的生存曲线可见，从随访开始，肺癌的生存率逐渐下降，见图16。

本例Cox模型表达式为：\mathrm{H}(\mathrm{t})=\mathrm{H}_{0}(\mathrm{t}) \cdot \times \cdot e^{-0.5078×(sex=2)+0.1602×(age_Median=2)-0.4053×(ph.karno_Median=2)}

预后指数(Prognostic Index，PI)是指H(t)指数部分，即-0.5078×(sex=2)+0.1602×(age_Median=2)-0.4053×(ph.karno_Median=2) 。PI越大，则风险函数H(t)越大，预后相对越差；反之，PI越小，预后越好。可按适当的PI分数将观察对象分为若干组(2~5组)，如低危组、中危组和高危组，以考察PI范围不同，其生存率的差异，对制定更合理的个体化治疗方案、正确指导患者的治疗、提高长期生存率有着重要意义。

如果对各变量进行标准化变换\left(\frac{x-\bar{x}}{s}\right)后再拟合Cox模型，则可得到标准化的预后指数(PI’)，当PI’=0时，表示该患者的死亡风险达到平均水平；当标准化PI’>0时，表示该患者的死亡风险高于平均水平；当标准化PI’<0时，表示该患者的死亡风险低于平均水平。 单击结果窗口右下角的“保存预示指数”超链接，打开保存预示指数对话框，见图17。

列：选择保存PI的列。

仅列出空列：仅列出没有数据的列。

标题：设定保存PI的列的标题(即变量名)。本例数据文件的指定列将增加一个变量“COXPH_P11(预后指数)”

四、结论

本研究采用Cox比例风险模型探究年龄、性别、卡氏评分与肺癌患者生存结局的关系，数据样本量满足要求，变量之间不存在多重共线性，对连续性变量进行分类转换后满足PH假设。多因素Cox回归分析显示，性别和卡氏评分分组与生存结局之间存在统计学关联(P<0.05)，年龄分组与生存结局之间不存在统计学关联(P=0.3198)。对于肺癌患者，女性肺癌患者死亡风险比男性低39.82% (HR=0.6018, 95%CI 0.4304~0.8415)；卡氏评分高的癌患者死亡风险比卡氏评分低组要低33.33% (HR=0.6667, 95%CI: 0.4841~0.9183)。

五、知识小贴士

(一) PH假设的判定

PH假设检验可以通过以下4种方法判断：

分类协变量的Kaplan-Meier生存曲线间无交叉。

利用Schoenfeld残差法查看连续性变量对应的P值和残差图。

绘制log cumulative hazard curve(对数累积风险曲线)，曲线平行是满足PH假定的充分且必要条件。可将每个协变量与对数生存时间的交互作用项放入模型中，如果交互项统计学上不显著，则满足等比例风险条件。

(二) 不满足PH假设的处理方法

若不满足PH假设，可以采用以下方法进行数据分析：

将不成比例关系的自变量作为分层变量，然后再用其余自变量进行多个Cox回归模型分析。

采用参数回归模型替代Cox回归模型。

改用含时间依存协变量的Cox比例模型。

MedCalc软件进行PH检验以及交互作用分析均不是很方便，建议更复杂的操作可以选择其他统计学分析软件。