医学研究中在进行生存分析(Survival Analysis)时,可使用Kaplan-Meier法进行单个分类变量的生存率比较。为了同时分析众多变量对生存时间和生存结局的影响,常采用多因素生存分析法。多因素生存分析法主要有参数模型和半参数模型两类。参数法需要以特定分布为基础建立模型,应用有局限性;而半参数法的假定相对较少,例如时间依存Cox回归模型(Time-Dependent Cox Regression Model)。本篇文章将举例介绍时间依存Cox回归模型进行多因素生存分析的适用条件及检验假设。
关键词:Cox等比例回归; Cox回归; 生存分析; 等比例风险; 含时间依存协变量; 时依协变量
一、适用条件
条件1:因变量是含有时间信息的二分类变量。本案例中因变量是包含生存时间的二分类资料,time是生存时间(天);status是生存结局。本案例数据满足该条件。
条件2:各观测值之间相互独立,无互相干扰。由数据和研究设计可知,该条件满足。
条件3:一般要求结局事件的样本量为自变量个数的10~20倍(EPV原则)。该条件需要软件分析来判断。
条件4:自变量之间无严重多重共线性。该条件需要软件分析来判断。
条件5:等比例风险(Proportional hazards,PH)假设,该条件需要软件分析来判断。
二、Cox比例风险回归模型
(一) Cox回归模型的基本形式
Cox比例风险回归模型简称Cox回归模型,由英国统计学家Cox于1972年提出,模型的基本形式为
\(h(t, X)=h_{0}(t) \exp \left(\beta^{\prime} X\right)=h_{0}(t) \exp \left(\beta_{1} X_{1}+\beta_{2} X_{2}+\beta_{1}+\beta_{m} X_{m}\right)\)
其中h(t, X)是具有协变量X的个体在时刻t时的风险函数,又称瞬时死亡率。t为生存时间,X=(X1,X2,…,Xm)'是可能影响生存时间的有关因素,也称协变量。这些变量可以是定量的,也可以是定性的,在整个观察期间内不随时间的变化而变化。h0(t)是所有协变量取值为0时的风险函数,称为基线风险函数(baseline hazard function)。β=(β1,β2,…,βm)'为Cox模型的回归系数,是一组待估的回归参数。
由于基本模式的公式右侧的h0(t)不需要服从特定的分布形状,具有非参数的特点,而指数部分exp(β'X)具有参数模型的形式,故Cox模型又称为半参数模型(semi-parametric model)。
如果采用生存率表示,则模型可写为:
\(S(t, X)=S_{0}(t)^{\exp \left(\beta^{\prime} X\right)}=S_{0}(t)^{\exp \left(\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m} X_{m}\right)}\)
其中S(t, X)是具有协变量X的个体在时刻t时的生存率,S0(t)为在时刻t的基线生存率,其他符号与上述公式相同。
(二) 参数的估计与假设检验
借助偏似然函数(partial likelihood function),采用最大似然估计获得Cox回归模型参数。在生存时间ti上,病人死亡的条件概率为:
\(q_{i}=\frac{h_{0}(t) \exp \left(\beta_{1} X_{\mathrm{i} 1}+\beta_{2} X_{\mathrm{i} 2}+\cdots+\beta_{m} X_{i m}\right)}{\sum_{S \in R\left(t_{i}\right)} h_{0}(t) \exp \left(\beta_{1} X_{\mathrm{s} 1}+\beta_{2} X_{\mathrm{s} 2}+\cdots+\beta_{m} X_{s m}\right)}\)
将k个生存时点的死亡条件概率相乘,得偏似然函数的计算公式为:
\(L=q_{1} q_{2} \cdots q_{k}=\prod_{i=1}^{k} q_{i}=\prod_{i=1}^{k} \frac{\exp \left(\beta_{1} X_{\mathrm{i} 1}+\beta_{2} X_{\mathrm{i} 2}+\cdots+\beta_{m} X_{i m}\right)}{\sum_{S \in R\left(t_{i}\right)} \exp \left(\beta_{1} X_{\mathrm{s} 1}+\beta_{2} X_{\mathrm{s} 2}+\cdots+\beta_{m} X_{s m}\right)}\)
式中qi为第i死亡时点的条件死亡概率,其分子部分为第i个个体在ti (t1≤t2≤…≤ti≤tk)死亡时点的风险函数h(ti);分母部分为处于风险的个体,即生存时间T≥Ti的所有(既包括死亡,也包括删失)个体的风险函数之和\(\sum_{j=i}^{n} h_{j}(t)\)。
分子分母中的基线风险函数h0(t)正好抵消, h0(t)无论等于多少,都对偏似然函数的结果不产生影响。一般的似然函数应包含所有n个个体点,而公式只含有k个死亡时点,忽略了删失时点的似然函数,故称之为偏(或部分)似然函数。
对偏似然函数取对数,得到对数似然函数lnL,求lnL关于βj(j=1, 2, …, m)的一阶偏导数,并求\(\frac{\partial \ln L}{\partial \beta_{j}}=0\)的解,便可获得βj的最大似然函数估计值bj。通常用Newton-Raphson迭代法求解这一偏似然方程组。
常用的回归系数检验方法有似然比检验、Wald检验和得分检验。
(三) 参数的意义及其解释
1.回归系数与相对危险度
由上述公式可以得到
\(h(t, X) / h_{0}(t)=\exp \left(\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m} X_{m}\right)\)
或
\(\ln \left[h(t, X) / h_{0}(t)\right]=\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m} X_{m}\)
βj与风险函数h (t, X)之间有如下关系:
①βj>0,则Xj取值越大时,h (t, X)的值越大,表示患者死亡的风险越大;
②βj<0,则Xj取值越大时,h (t, X)的值越小,表示患者死亡的风险越小;
③βj=0,则Xj取值对h (t, X)没有影响。
两个分别具有协变量Xi与Xj的个体,其风险函数(亦称为危险度)之比称为相对危险度(risk ratio,RR)或风险比(hazard ratio,HR),是一个与时间无关的量,即:\(h\left(t, X_{i}\right) / h\left(t, X_{j}\right)=\exp \left[\beta\left(X_{i}-X_{j}\right)\right]\)
如Xi是暴露组观察对象对应各因素的取值,Xj是非暴露组观察对象对应各因素的取值,求得β的估计值后,则根据上述公式可以求出暴露组对非暴露组的相对危险度估计值。
βj的流行病学含义是:在其他协变量不变的情况下,协变量Xj每改变一个测定单位时所引起的相对危险度的自然对数的改变量。
当协变量Xj取值为0,1时,按上述公式其对应的\(\widehat{R R}\)为:
\(\widehat{R R}=\exp \left(b_{j}\right)\)
当协变量取值为连续性变量时,用Xj和\(X_{j}{ }^{*}\)分别表示在不同情况下的取值,按公式则其对应的\(\widehat{R R}=\exp \left(b_{j}\right)\)为:
\(\widehat{R R}=\exp \left[b_{j}\left(X_{j}-X_{j}^{*}\right)\right]\)
RR的1-α可信区间为
\(\exp \left(b_{j} \pm z_{\alpha / 2} \times S_{b_{j}}\right)\)
2. 个体预后指数
Cox回归模型的线性部分\(\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m} X_{m}\)与风险函数h(t)成正比,即风险越大,\(\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m} X_{m}\)也越大,因此模型的线性部分反映了一个个体的预后,称\(P I=\beta_{1} X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m} X_{m}\)为预后指数(prognosis index,PI)。预后指数越大,患者风险越大,预后越差;反之,预后指数越小,预后越好。
如果对各变量进行标准化转换后再拟合Cox模型,则可得到标准化的预后指数,当标准化PI'=0时,表示该患者的死亡风险达到平均水平;当标准化PI'>0时,表示该患者的死亡风险高于平均水平;当标准化PI'<0时,表示该患者的死亡风险低于平均水平。
(四) 比例风险假定的检验
Cox比例风险回归模型的主要前提条件是假定风险比值h (t)/h0 (t)为固定值,即协变量对生存率的影响不随时间的改变而改变。只有该条件得到满足,Cox回归模型的结果才有效。检验这一假定条件的方法有:
1. 如果分类协变量的每一组别的Kaplan-Meier 生存曲线间无交叉,则满足比例风险假定。
2. 以生存时间t为横轴,对数生存率\(\ln [-\ln \hat{S}(t)]\)
为纵轴,绘制分类协变量每一组别的生存曲线,如果协变量各组别对应的曲线平行,则满足风险比例条件。
3. 对于连续型协变量,可将每个协变量与对数生存时间的交互作用项(X ln(t))放入回归模型中,如果交互作用项无统计学意义,则满足风险比例条件。
当风险比例的假定条件不成立时,可采用如下方法来解决:
1. 将不成比例关系的协变量作为分层变量,然后再用其余变量进行多因素Cox回归模型分析。
2. 采用参数回归模型替代Cox回归模型进行分析。
3. 对于连续型协变量,可将每个协变量与对数生存时间的交互作用项(X ln(t))放入回归模型中。
三、Cox比例风险回归模型实例
(一) 案例介绍
某肿瘤研究所收集了200例肺癌患者的生存数据:包括生存状态(status,1=“删失”,2=“死亡”)、生存时间(time,天);性别(sex,1=“男”,2=“女”)、年龄 (age,岁)和卡氏评分(ph.karno),部分数据见图1。现欲探究患者的性别、年龄、卡氏评分与生存结局的关系。
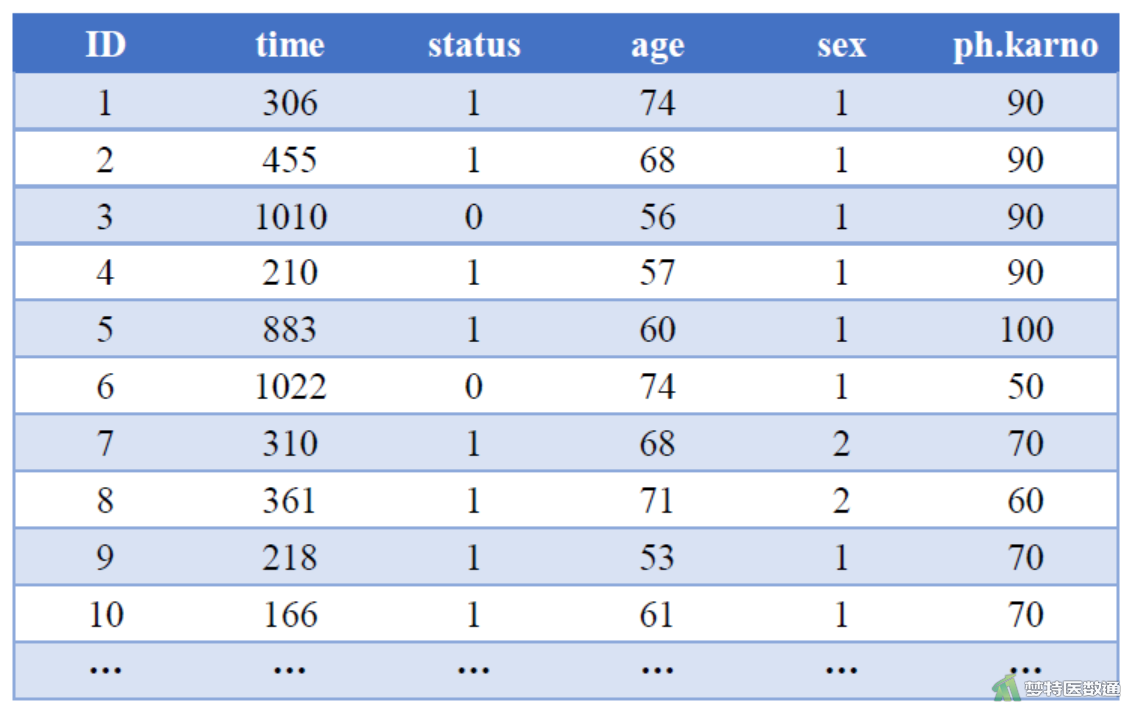
(二) 多因素Cox回归分析
1. 等比例风险检验
对多因素Cox比例风险模型中的自变量进行PH假定检验(图2),结果显示整体检验P值<0.05,提示模型中存在不满足PH假定的变量。进一步查看各变量的PH假定检验结果,发现年龄(age)和性别(sex)的P值>0.1,而卡氏评分(ph.karno)的P值<0.05,提示年龄和性别满足PH假定,卡氏评分不满足PH假定。若不满足PH假定,则需要改用含时间依存协变量的Cox比例模型分析数据。
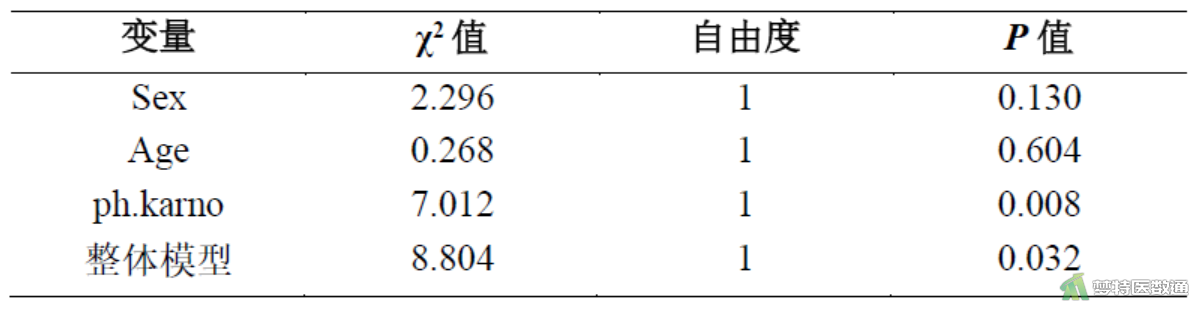
2. 含时间依存协变量的Cox比例风险模型
构建包含ph.karno时间依存协变量(T_COV_=ln(t+20))的Cox比例风险模型,结果如图3所示。分析结果显示,性别的效应值HR为0.616,表示女性死亡的风险比男性低38.4% (HR=0.616,95%CI:0.441~0.861;P=0.005),年龄与生存结局的关联无统计学意义 (HR=1.013,95%CI:0.994~1.032;P=0.197)。卡氏评分的时依系数β(t)= -0.094+0.015×ln(t+20),效应值HR=exp(-0.094+0.015×ln(t+20))。例如,当时间为200天时,卡氏评分对应的HR=exp(-0.094+0.015×ln(200+20))= 0.987。

四、因素的初步筛选与最佳模型的构建
(一) 因素的筛选
影响生存时间的因素称为协变量,当协变量较多时,在建立模型之前可对这些协变量进行筛选,即可进行Cox回归模型单因素分析。单变量分析筛选出的有统计学意义的变量,可继续进行多因素Cox回归模型分析。另外,如果某些协变量有明确的专业意义,无论它们在单因素分析中有无统计学意义均可纳入模型。如果研究的协变量不多,也未发现变量之间有明显的共线性,也可以直接将各协变量纳入模型进行逐步Cox回归模型分析。
(二) 最佳模型的建立
为建立最佳模型常需对研究的因素进行筛选,筛选因素的方法有前进法、后退法和逐步回归法,实际工作中要根据具体情况选择使用。在逐步筛选变量建立多因素Cox回归模型时需规定检验水准,以确定方程中引入哪些因素和剔除哪些因素,一般情况下确定引入检验水准为0.05,剔除检验水准为0.1,剔除水准应大于等于引入水准,以便引入后的变量不易被剔除。如果研究课题要求特别严格,可将引入检验水准定为0.01;如果研究课题要求比较宽松,可将引入检验水准定为0.2。检验各因素是否有统计学意义的方法有似然比检验、Wald检验和计分检验,在实际工作中可根据具体的情况而定。