在前面文章中使用一般线性模型实现裂区设计(Nested Design)资料的方差分析,对于两因素裂区设计其实等价于两因素重复测量设计。本文将实例演示在SPSS软件中通过重复测量方差分析实现裂区设计资料的方差分析的操作步骤。
关键词:SPSS; 裂区设计; 分割设计; 一般线性模型; 方差分析; 重复测量; 重复测量方差分析
一、案例介绍
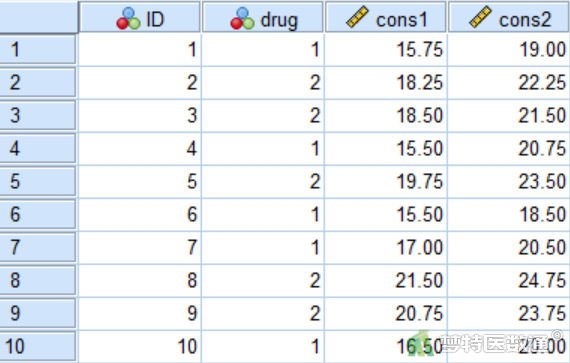
本例采用“裂区设计(Nested Design)资料的方差分析(一)—SPSS软件实现”案例。研究一种全身抗毒素对皮肤损伤的保护作用,将10只家兔随机分为2组,一组注射抗毒素,一组注射生理盐水。每组家兔取甲、乙两部位,分别以高低两种浓度注射,观察指标为皮肤损伤直径(mm)。不过重复测量方差分析对数据的整理格式不同于一般线性模型,数据见图1。其中ID为家兔编号,drug为注射物(1=抗毒素,2=生理盐水),cons1为低浓度时的损伤直径(mm),cons2为高浓度时的损伤直径(mm);本案例数据可从“附件下载”处下载。
二、问题分析
本案例是完全随机裂区设计的方差分析,其中一个因素为注射物,另一个因素为药物浓度,药物浓度是按照家兔不同部位进行分配(属于区组因素),可以被认为是重复测量因素。因此,可以按照两因素重复测量方差分析进行数据分析。
三、软件操作及结果解读
关于两因素重复测量方差分析的适用条件判断详见“两因素重复测量方差分析(Two-way Repeated-Measures, ANOVA)一——无交互作用——SPSS软件实现(链接)”,本文主要演示主体分析过程和结果。
(一) 重复测量方差分析过程
1. 调用“重复测量窗口”
选择“分析”—“一般线性模型”—“重复测量”(图2)。
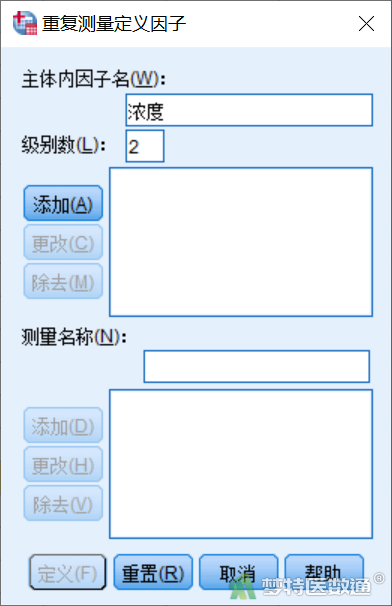
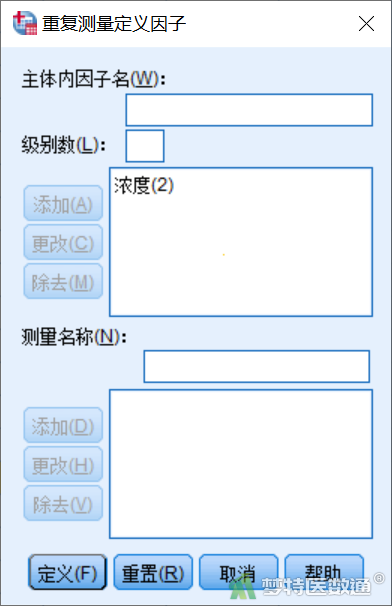
打开“重复测量定义因子”对话框(图3),在“主体内因子名”处录入重复测量的因子名称,自定义名称。由于本案例是在2个浓度的重复测量,所以此处将“因子 1”改为“浓度”;下方“级别数”填入测量次数,本例填“2”,点击“添加”(图4),再点击“定义”。
打开“重复测量”对话框(图5),将cons1、cons2分别选入右侧“主体内变量”中,将drug选入右侧“主体间因子”中,此后的软件操作都基于该窗口。
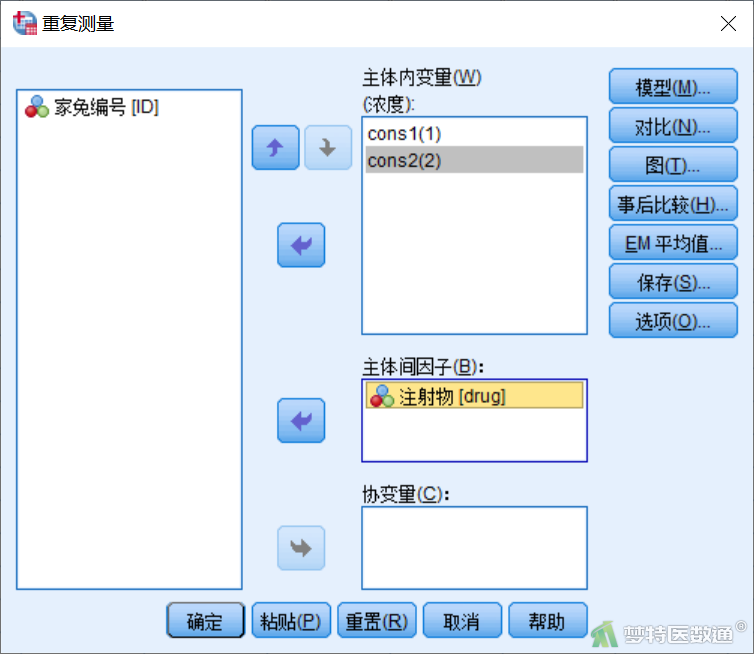
2. “重复测量窗口”设置
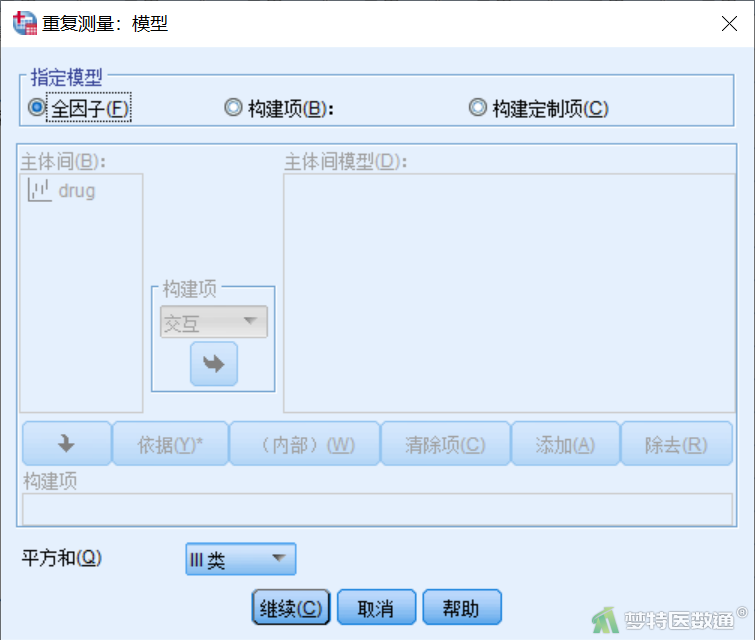
点击“重复测量”对话框(图5)右侧“模型”,打开“重复测量:模型”子对话框(图6),保持默认,即全因子模型,因为需要分析交互作用。
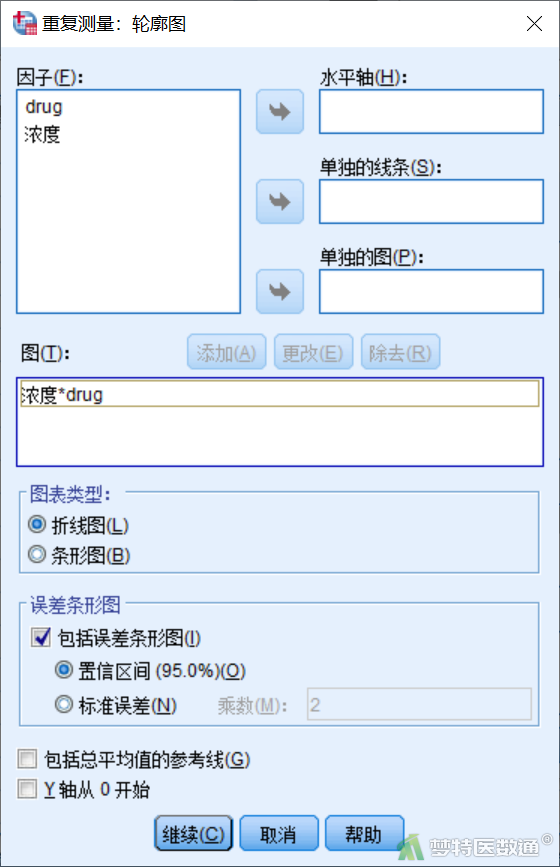
点击“重复测量”对话框(图5)右侧“图”,打开“重复测量:轮廓图”子对话框(图7),将“浓度”选入右侧“水平轴”中,将“drug”选入右侧“单独的线条”中,然后点击“添加”,在“图表类型”项中保持选中“折线图”,在“误差条形图”项中勾选“包括误差条形图”及“置信区间(95.0%)”,点击“继续”。
点击“重复测量”对话框(图5)右侧“EM平均值”,打开“重复测量:估算边际均值”子对话框(图8),将drug、“浓度”和“drug*浓度”选入右侧“显示下列各项的均值”中,点击“继续”。

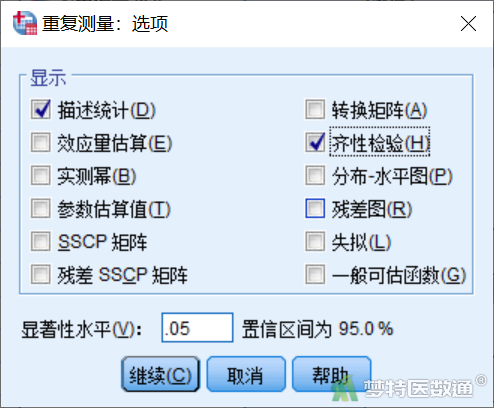
点击“重复测量”对话框中(图5)右侧“选项”,打开“重复测量:选项”子对话框(图9),勾选“描述统计”和“齐性检验”,点击“继续”。回到图5后,点击“确定”即可。
(二) 结果解读
1. 统计描述/估算边际平均值
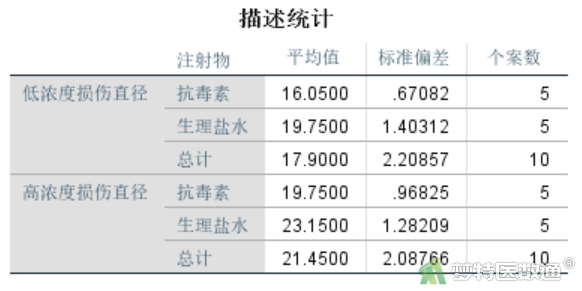
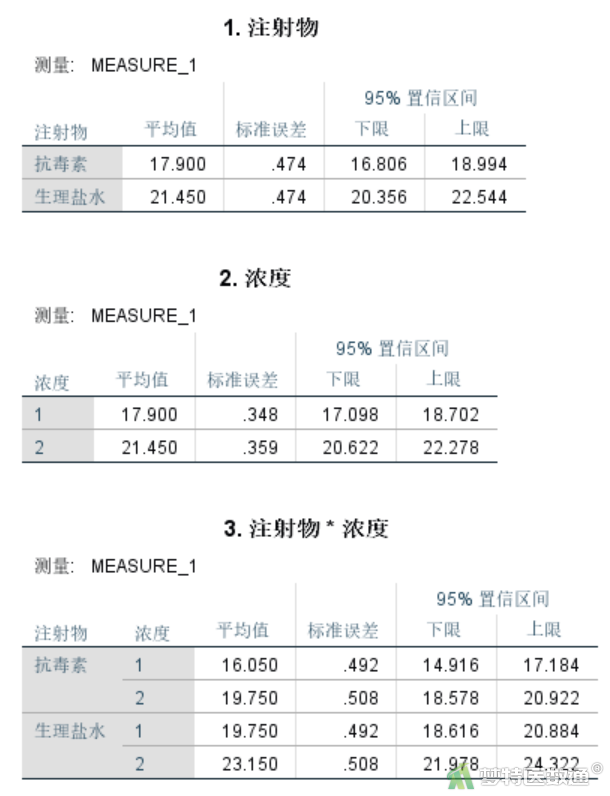
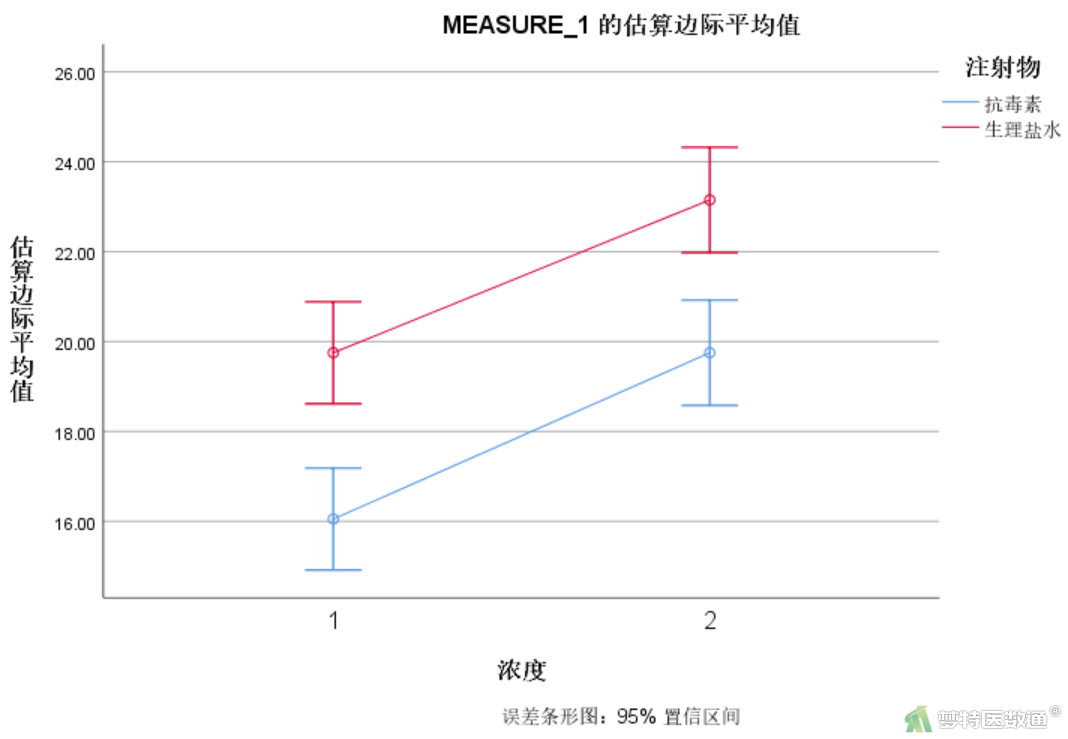
“描述统计”结果(图10)和“估算边际平均值”结果(图11)一致。列出了不同注射物和不同浓度实验条件下的皮肤损伤均数、标准差、95%置信区间以及“浓度”和“注射物”各种组合下的皮肤损伤均数。边际均值图见图12。
2. 方差分析
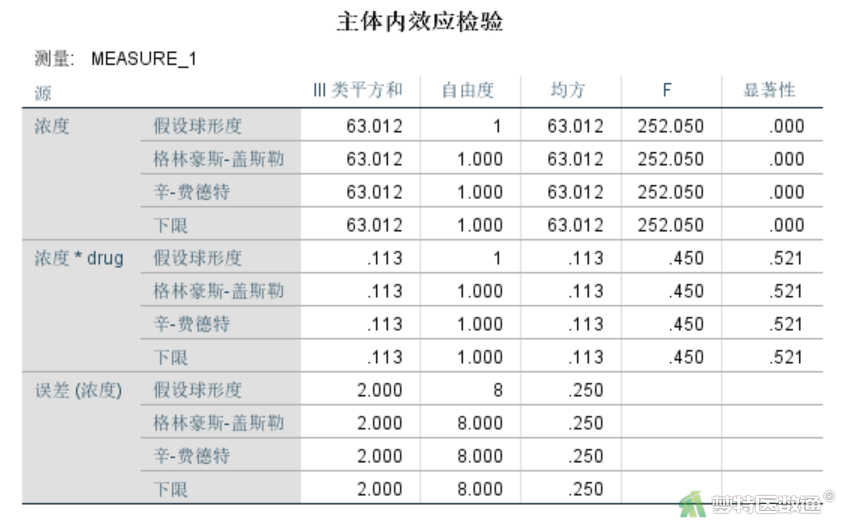
“主体内效应检验”结果(图13)提示,不同浓度间皮肤损伤面积有统计学差异(F=252.050,P<0.001),结合统计学描述结果可知,低浓度的损伤程度比高浓度轻。注射物与浓度间的交互作用无统计学意义(F=0.450,P=0.521)。结果与一般线性模型分析完全一致。
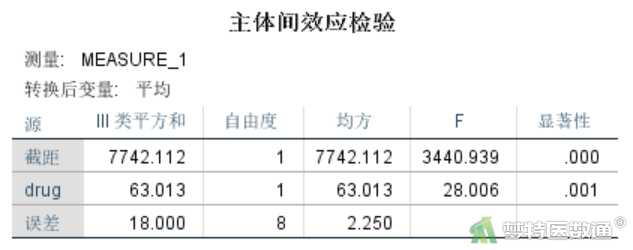
“主体间效应检验”结果(图14)可知,不同注射物间皮肤损伤面积有统计学差异(F=28.006,P=0.001),结合统计学描述结果可知抗毒素的损伤程度比生理盐水轻。结果与一般线性模型分析完全一致。
四、结论
本研究采用裂区设计研究一种全身抗毒素对皮肤损伤的保护作用。采用两因素重复测量方差分析结果显示,不同注射物间皮肤损伤面积有统计学差异(F=28.006,P=0.001),抗毒素的损伤程度[17.90 (95%CI 16.81~19.00)]比生理盐水[21.45 (95%CI 20.36~22.54)]轻。不同浓度间皮肤损伤面积有统计学差异(F=252.050,P<0.001),低浓度的损伤程度[17.90 (95%CI 17.10~18.70)]比高浓度[21.45 (95%CI 20.62~22.28)]轻。注射物与浓度间的交互作用无统计学意义(F=0.450,P=0.521)。