裂区设计(Split-plot design)又称分割设计,是析因设计的一种特殊形式,是把一个或多个完全随机设计、随机区组设计或拉丁方设计结合起来的实验方法。本文将实例演示在SPSS软件中通过一般线性模型实现裂区设计资料的方差分析的操作步骤。
关键词:SPSS; 裂区设计; 分割设计; 一般线性模型; 方差分析
一、案例介绍
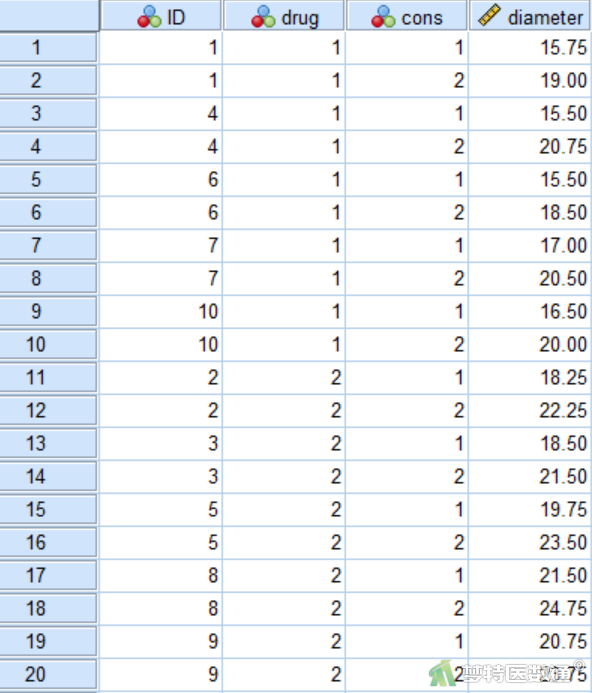
研究一种全身抗毒素对皮肤损伤的保护作用,将10只家兔随机分为2组,一组注射抗毒素,另一组注射生理盐水。每组家兔取甲、乙两部位,分别以高低两种浓度注射,观察指标为皮肤损伤直径(mm),部分数据见图1,其中ID为家兔编号,drug为注射物(1=抗毒素,2=生理盐水),cons为浓度(1=低浓度,2=高浓度),diameter为损伤直径(mm);本案例数据可从“附件下载”处下载。
二、问题分析
本案例是完全随机裂区设计的方差分析,一级实验单位为家兔,二级实验单位为注射部位,可以按照多因素方差分析进行数据分析。
三、软件操作及结果解读
(一) 一般线性模型分析过程
选择“分析”—“一般线性模型”—“单变量”(图2)。
在“单变量”对话框(图3)中,将diameter选入右侧“因变量”,drug、cons选入右侧“固定因子”,ID选入“随机因子”。
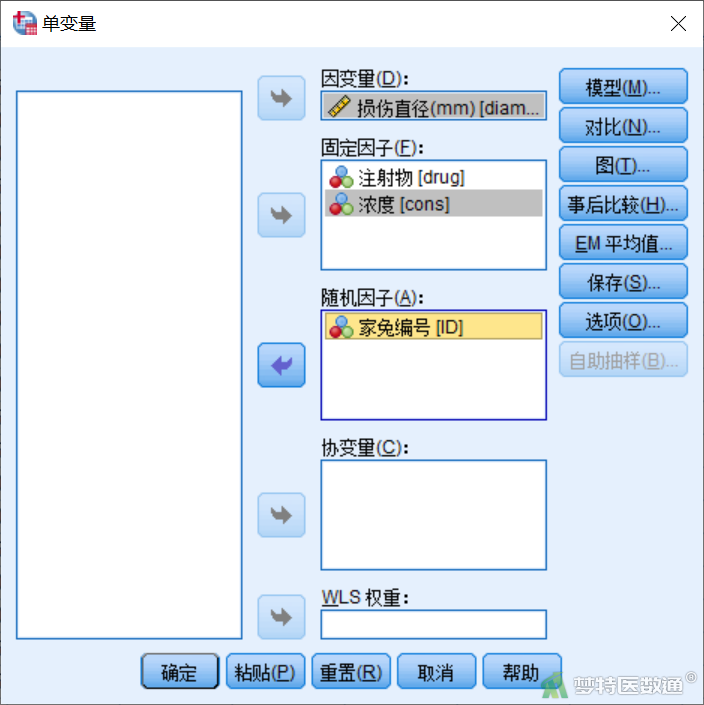
点击图3右侧“模型”,进入“模型”子对话框(图4),点击“构建项”,将drug、cons的主效应,cons*drug的交互项以及ID(drug)嵌套项选入右侧“模型”,ID(drug)嵌套项可通过“构建定制项”设定。
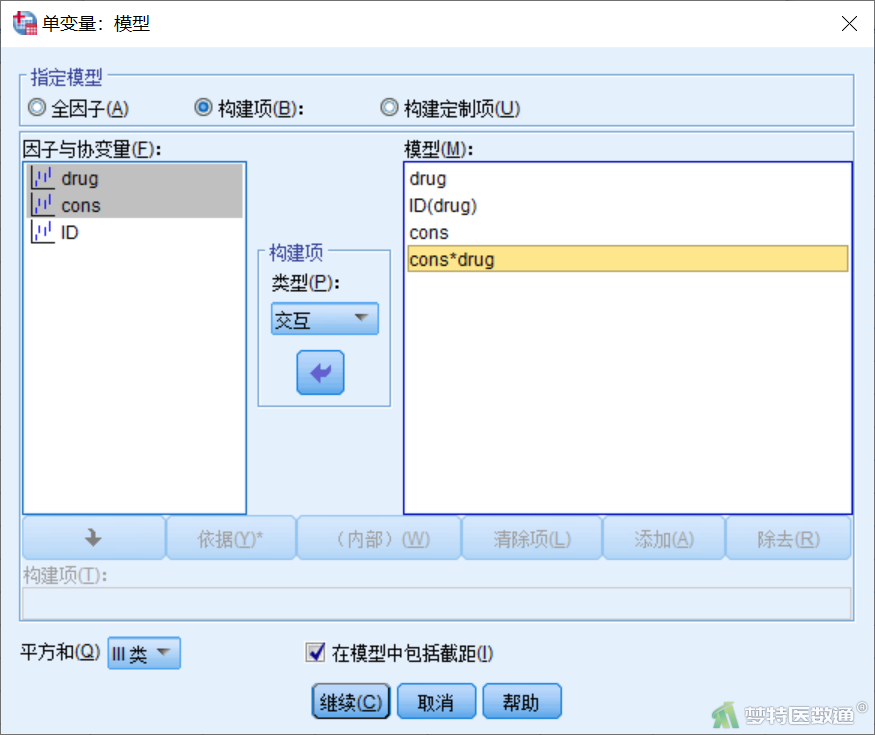
点击图3右侧“EM平均值”,进入“估算边际平均值”子对话框(图5),将drug、cons、cons*drug选入右侧“显示下列各项的均值”。
点击图3右侧“选项”,进入“选项”子对话框(图6),勾选“描述统计”。
(二) 结果解读
1. 统计描述/估算边际平均值
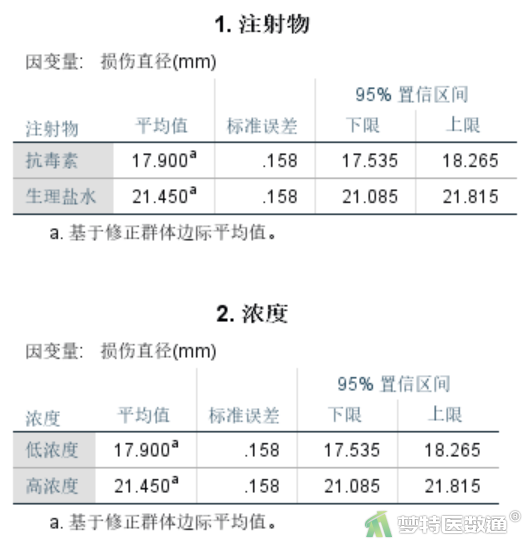
“描述统计”结果见图7,其列出了不同注射物和不同浓度实验条件下的皮肤损伤直径均数和95%置信区间。图8列出了“浓度”和“注射物”各种组合下的皮肤直径均数。
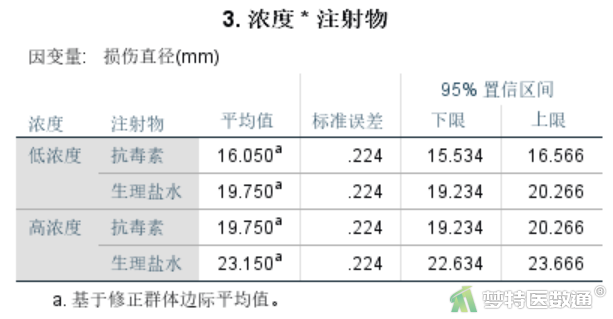
2. 方差分析
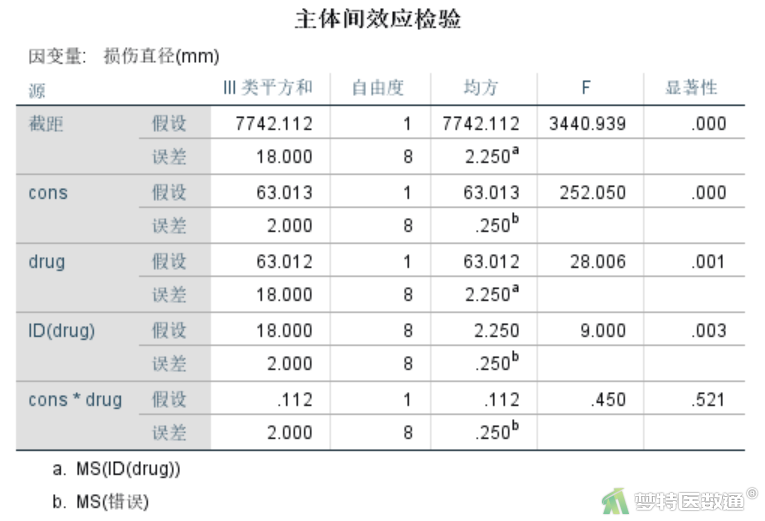
“主体间效应检验”结果(图9)显示,不同注射物间皮肤损伤直径比较,差异有统计学差异(F=28.006,P=0.001),结合图7可知抗毒素的损伤程度比生理盐水轻。不同浓度间皮肤损伤直径比较,差异有统计学意义(F=252.050,P<0.001);低浓度的损伤程度比高浓度轻。注射物与浓度间的交互作用无统计学意义(F=0.450,P=0.521)。家兔间个体差异有统计学意义(F=9.000,P=0.003)。
四、结论
本研究采用裂区设计研究一种全身抗毒素对皮肤损伤的保护作用。分析结果显示,不同注射物间皮肤损伤直径比较,差异有统计学意义(F=28.006,P=0.001),注射抗毒素的损伤程度[17.90 (95CI 17.53~ 18.26)]比生理盐水轻[21.45 (95CI 21.08~21.81)]。不同浓度间皮肤损伤直径比较,差异有统计学意义(F=252.050,P<0.001),低浓度的损伤程度比高浓度轻。注射物与浓度间的交互作用无统计学意义(F=0.450,P=0.521)。