在SPSS中,完全随机设计(Completely Randomized Design)资料的方差分析既可以使用单因素方差分析模块,也可使用一般线性模型模块,还可以使用线性回归模块进行分析。本篇文章将实例演示在SPSS软件中通过一般线性模型模块实现完全随机设计资料的方差分析的操作步骤。
关键词:SPSS; 完全随机设计; 一般线性模型; 单因素方差分析; F检验; Welch检验; 韦尔奇检验; 事后检验; 两两比较
一、案例介绍
使用单因素方差分析(One-Way ANOVA)—SPSS软件实现相同案例。某医生用A、B、C 3种方案(group,1=A、2=B、3=C)治疗贫血患者,治疗两个月后,记录每名受试者血红蛋白的上升克数(Hb)。问3种方案治疗贫血患者的效果是否有差别?部分数据见图1。本案例数据可从“附件下载”处下载。
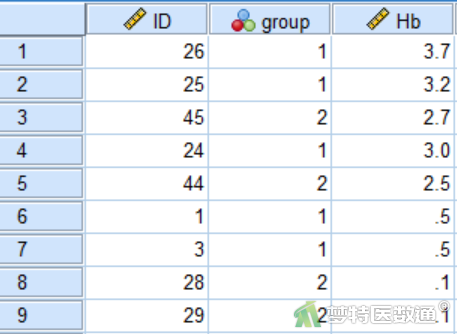
二、问题分析
本案例的分析目的是比较3种治疗方案对贫血患者的疗效是否有差别,即判断3种治疗方案患者的血红蛋白上升克数是否存在差异。针对这种情况可以使用一般线性模型进行数据分析。但需要满足6个条件:
条件1:观察变量为连续变量。本研究中的血红蛋白上升克数为连续变量,该条件满足。
条件2:观测值相互独立。本研究中各研究对象的观测值都是独立的,不存在互相干扰的情况,该条件满足。
条件3:观测值可分为多组(≥2)。本研究中分为A、B、C 3组,该条件满足。
条件4:观察变量不存在显著的异常值,该条件需要通过软件分析后判断。
条件5:各组观测值为正态(或近似正态)分布,该条件需要通过软件分析后判断。
条件6:多组观测值的整体方差相等,该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 适用条件判断
正态性、方差齐性除了可以按照单因素方差分析(One-Way ANOVA)—SPSS软件实现进行判断以外,在一般线性模型或线性回归中还可以通过残差进行判断,详见两因素方差分析(Two-way ANOVA)一——不存在交互作用——SPSS软件实现,异常值既可以通过残差进行判断,还可以通过库克距离进行判断。一般线性模型分析操作过程详见后文。
1. 条件4判断(异常值检测)
一般认为当库克距离(Cook′s distance)≤0.5时不是异常值点,当>0.5时是异常值点。通过一般线性模型生成的库克距离(变量COO_1)可知,最大库克距离为0.11<0.5,提示不存在显著异常值(图2)。
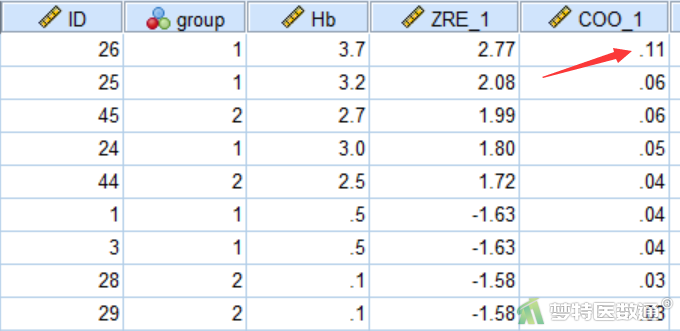
2. 条件5判断(正态性检测)
通过对一般线性模型生成的残差进行整体(不分组)正态性检验结果(图3)可知,柯尔莫戈洛夫-斯米诺夫(K-S检验)和夏皮洛-威尔克(S-W检验)两种正态性检验的结果,均P>0.05,均提示数据服从正态分布。
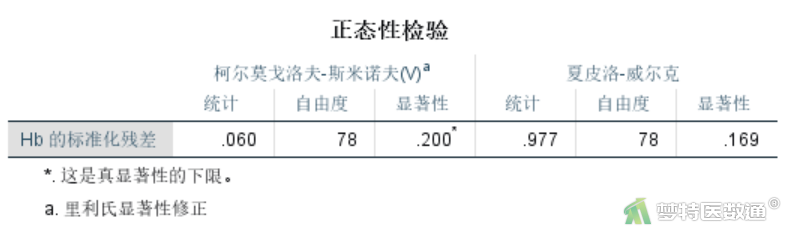
3. 条件6判断(方差齐性检验)
通过对一般线性模型分析中的方差齐性检验结果(图4)可知,基于平均值的F=2.610,P=0.080>0.05,提示3组数据方差齐(此时的检验水准取的0.05,如果取0.1也可认为方差不齐)。本案例如果描述“标准偏差”和“方差”结果见单因素方差分析(One-Way ANOVA)—SPSS软件实现一文,可知A、B、C3组的标准差分别为0.87、0.74、0.54 g,方差分别为0.75、0.55和0.29,也并非严重不齐,为保守起见,采用了校正单因素方差分析(韦尔奇检验),事后检验采用了“盖姆斯-豪厄尔”法。综合考虑,可认为满足方差齐性要求。
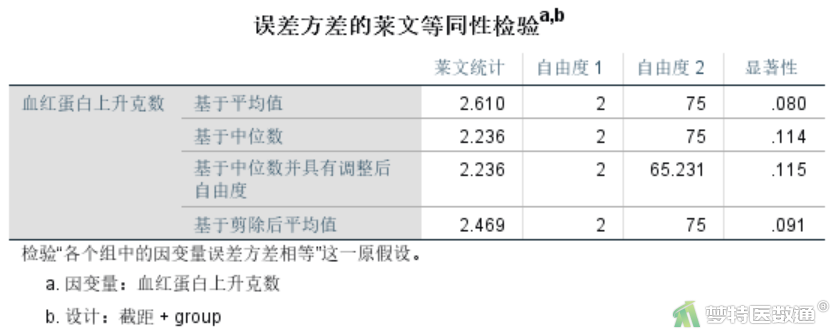
(二) 一般线性模型分析过程
选择“分析”—“一般线性模型”—“单变量”(图5)
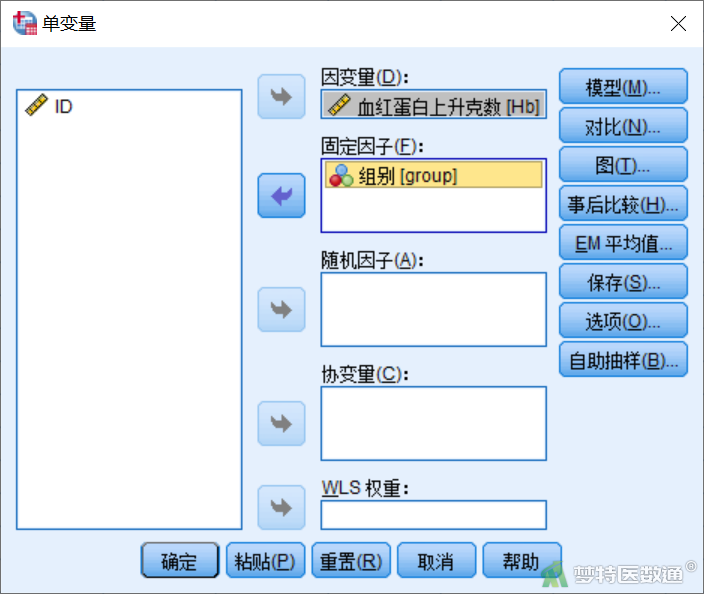
打开“单变量”对话框,将Hb选入右侧“因变量”框,将group选入右侧“固定因子”框(图6)。
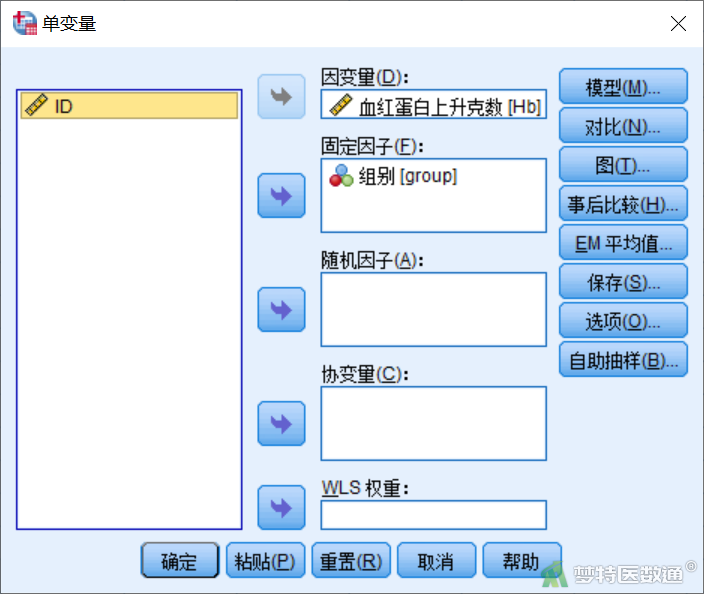
点击图6右侧“模型”,打开“单变量:模型”子对话框(图7),保持默认,即选择“全因子”。
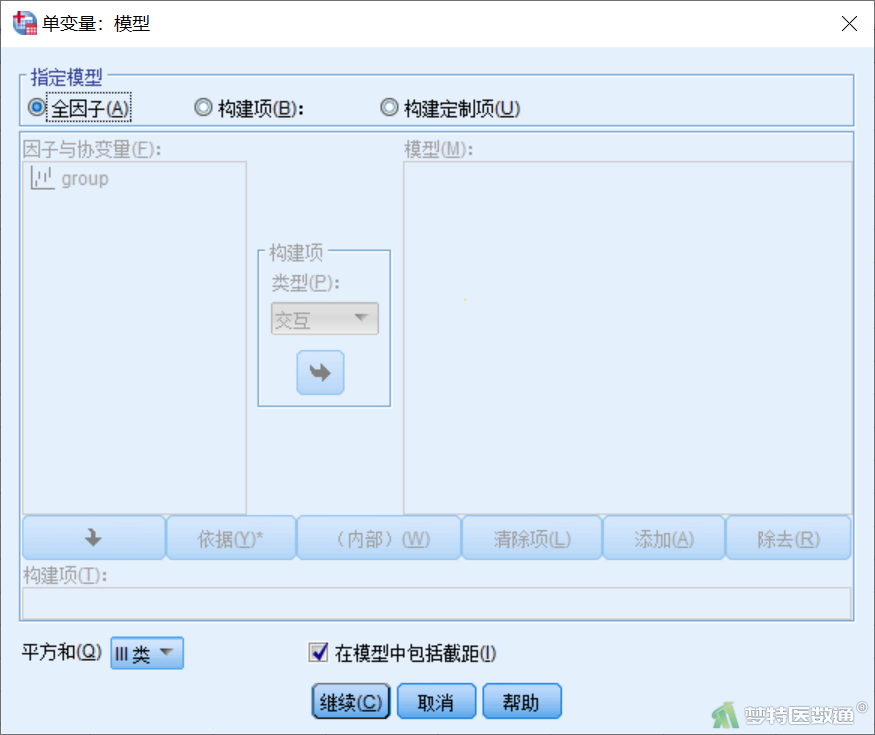
点击图6右侧“图”,打开“单变量:轮廓图”子对话框(图8),将group选入右侧“水平轴”,点击“添加”,选中下方的“折线图”以及“包括误差条形图”、“置信区间(95.0%)”。
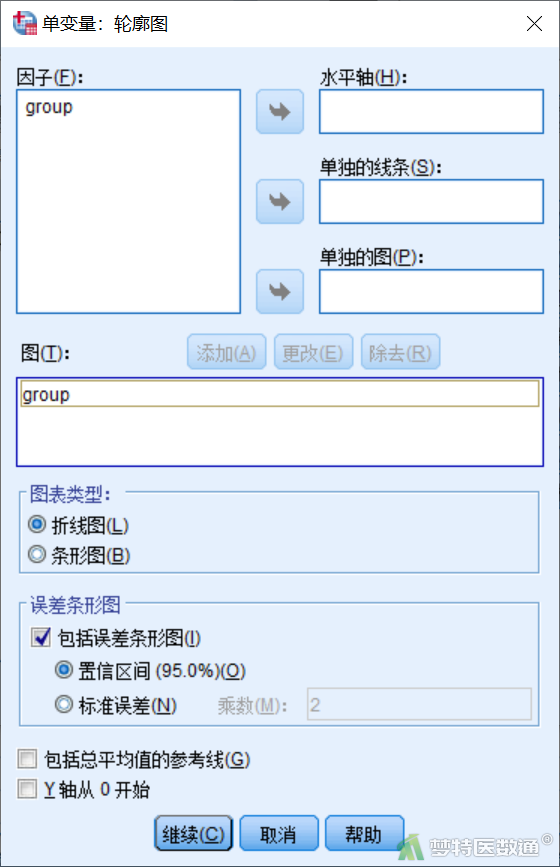
点击图6右侧“事后比较”,打开“单变量:实测平均值的事后多重比较”子对话框(图9),将group选入右侧“下列各项的事后检验”,两两比较勾选“盖姆斯-豪厄尔”法。
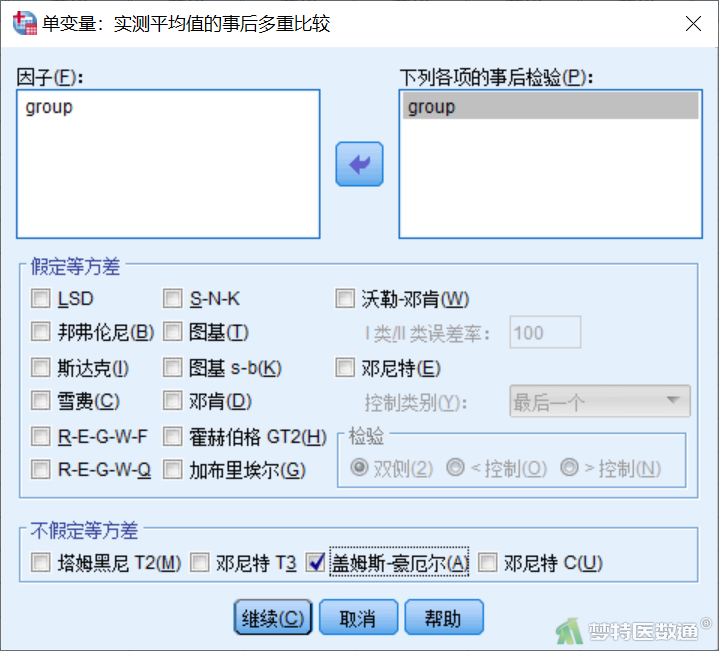
点击图6右侧“EM平均值”,出现“单变量:估算边际均值”子对话框(图10),将group选入右侧“显示下列各项的均值”框。
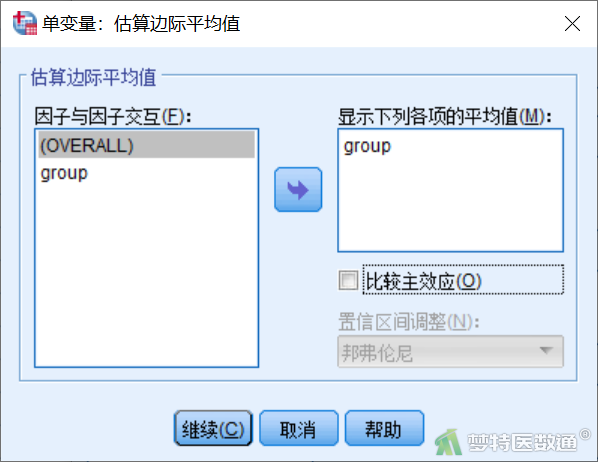
点击图6右侧“保存”,出现“单变量:保存”子对话框(图11),勾选“残差”下的“标准化”,“诊断”下勾选“库克距离”。
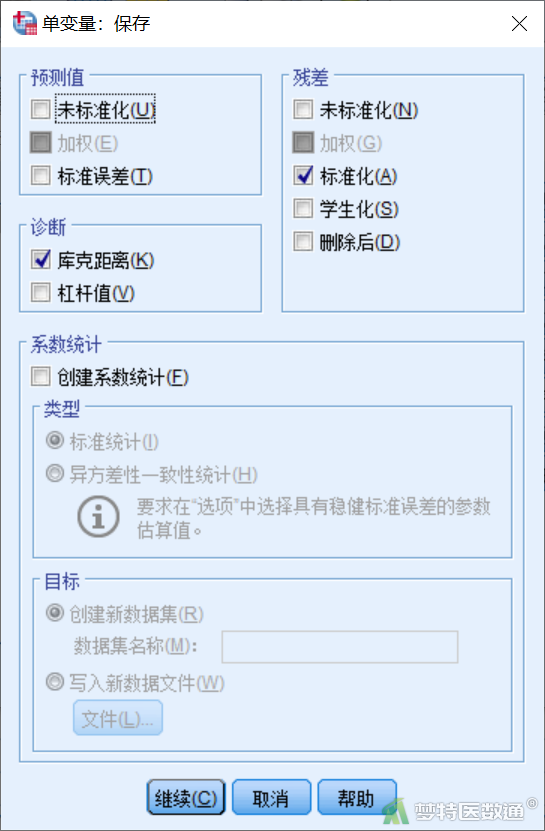
点击图6右侧“选项”,出现“单变量:选项”子对话框(图12),勾选“描述统计”“齐性检验”。点击“继续”回到图6,点击“确定”即可。
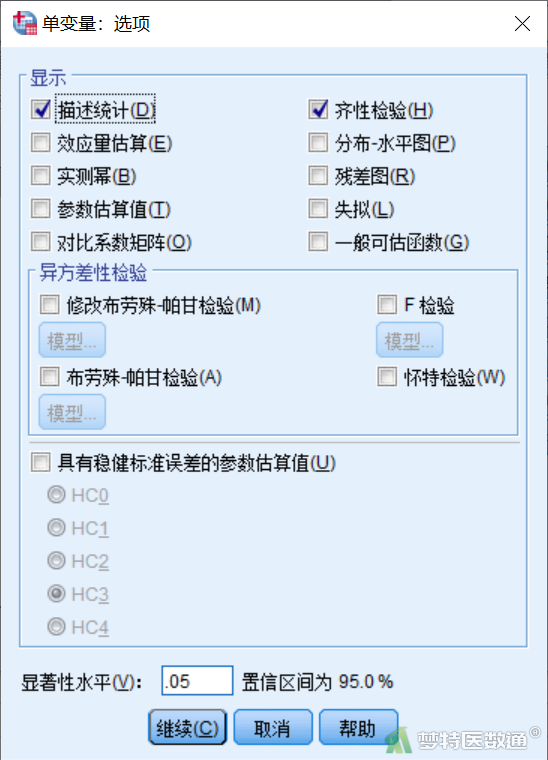
(三) 结果解读
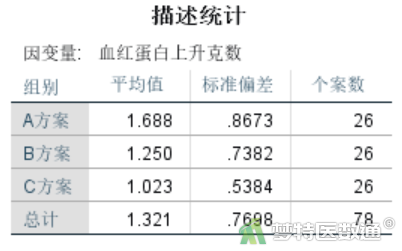
1. 统计描述
描述统计结果见图13,A、B、C3组血红蛋白的上升克数分别为1.69±0.87、1.25±0.74和1.02±0.54 g。3组数值不同,但判断差异是否存在统计学意义,还需要进一步进行统计学检验。
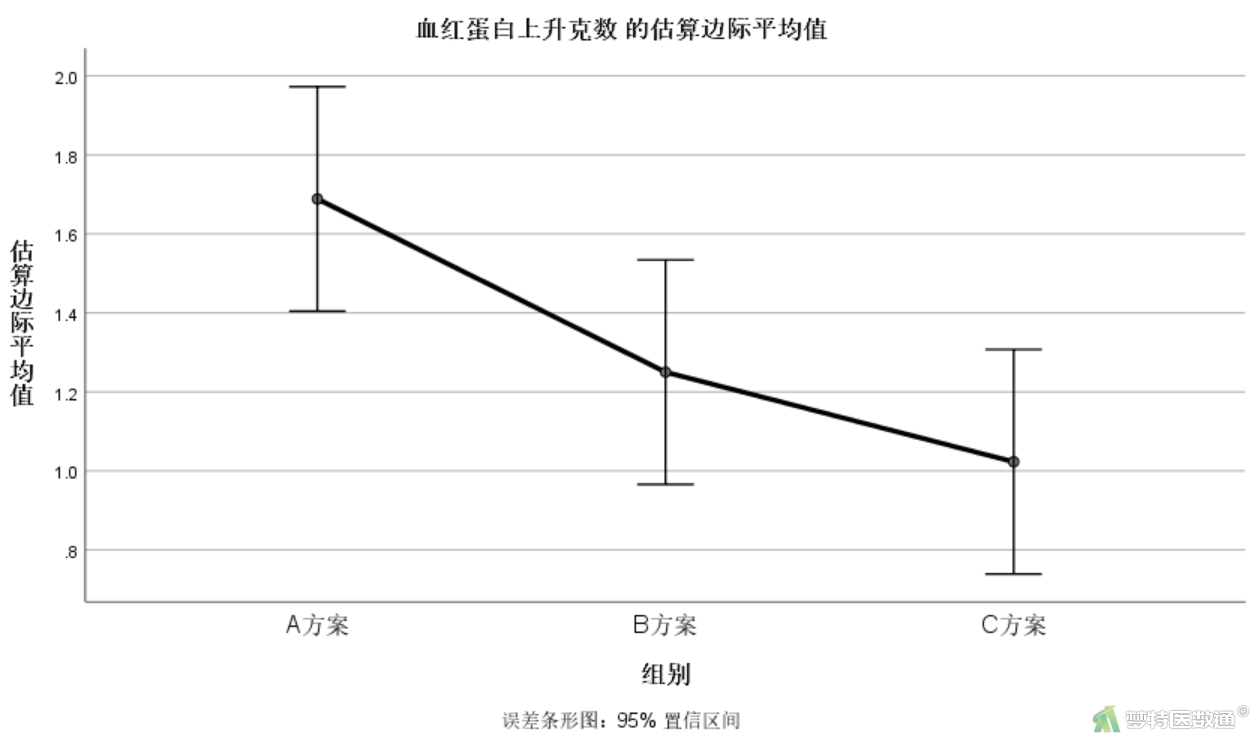
“血红蛋白上升克数的估算边际平均值”图(图14)绘制了各组血红蛋白上升克数的变化情况,可见3组数值不同。
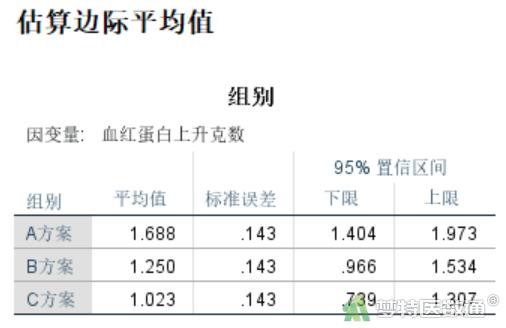
2. 估算边际平均值
当不存在协变量时,“估算边际平均值”结果(图15)和“统计描述”结果(图13)的均值一样。“估算边际平均值”同时给出了置信区间。
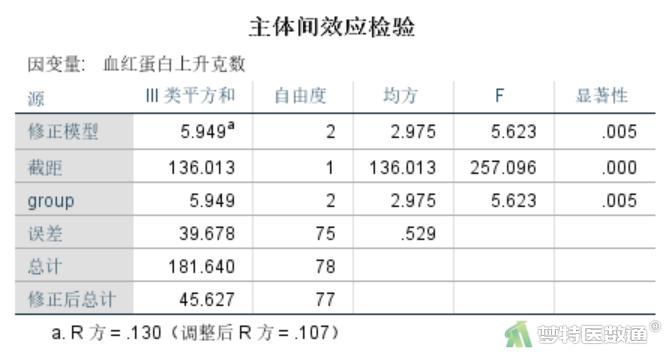
3. 方差分析
“主体间效应检验”结果(图16)提示,group的F=5.623,P=0.005;提示各组均数不全相等(至少有两组均数不相同),结果与未校正的单因素方差分析结果完全一致。
4. 多重比较
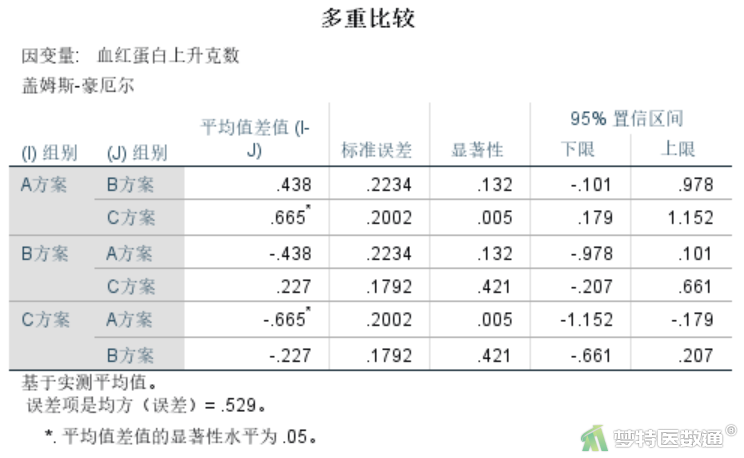
多重比较结果见图17,凡“显著性”一栏P<0.05,表示两者之间差异有统计学意义。结果显示可知,A组和B组之间的差异为0.438 g,但差异无统计学意义(P=0.132);A组和C组之间的差异为0.665 g,差异有统计学意义(P=0.005);B组和C组之间的差异为0.227 g,差异无统计学意义(P=0.421)。因此,可知A组血红蛋白的上升克数比C组高0.665 g,差异有统计学意义。
四、结论
本研究采用一般线性模型分析判断3种方案治疗患者贫血的血红蛋白上升克数是否存在差异。通过库克距离判断,3组数据不存在需要特殊处理的异常值;通过对残差进行正态性检验,提示3组数据服从正态分布;通过Levene’s检验,提示3组数据间方差齐。
分析结果显示,A、B、C3组血红蛋白的上升克数分别为1.69±0.87、1.25±0.74和1.02±0.54 g,3组均数不全相等(F=5.623,P=0.005)。进一步采用盖姆斯-豪厄尔法进行两两比较,显示A组血红蛋白的上升克数比C组高0.665 g,差异有统计学意义(P=0.005);A组血红蛋白的上升克数比B组高0.438 g,但差异无统计学意义(P=0.132);B组血红蛋白的上升克数比C组高0.227 g,但差异无统计学意义(P=0.421)。因此,A、B、C3种治疗方案对治疗贫血患者疗效不同,A方案疗效最好。