在前面文章中研究的因素可能是多个,但是重复测量因素只有一个,本文介绍存在两个重复测量因素(Two Repeated Measures Factor)且有交互作用的情况及其在R软件中的实现过程。
关键词:R; 重复测量; 重复测量资料; 重复测量方差分析; 两重复测量因素; 球形检验; 交互作用; 主效应; 单独效应
一、案例介绍
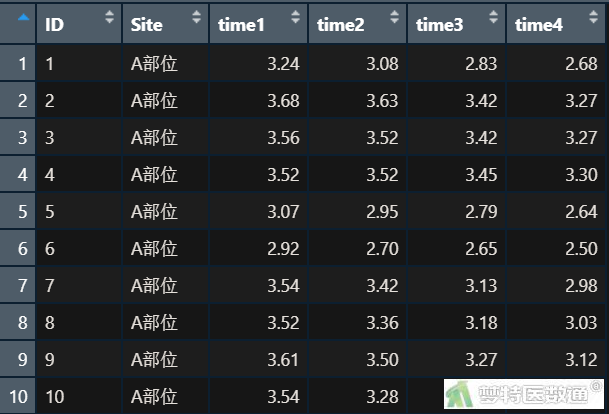
评价在某麻醉药物的作用下,不同部位某蛋白酶活性变化情况。在使用该种药物后,检测12只小白鼠用药后10、20、30、40min 4个不同时刻A部位和B部位蛋白酶的活性。数据见图1。本案例数据可从“附件下载”处下载。
二、问题分析
本案例资料具有两个重复测量因素,一个是时间因素,有4个水平,即time1~time4,分别代表用药后10、20、30、40min 4个不同时刻。另一个是身体不同部位,有2个水平,即A部位和B部位。因此需要使用两重复测量因素方差分析进行数据分析。需要满足以下5个条件:
条件1:观察变量唯一,且为连续变量。本研究中观察变量只有蛋白酶活性,且为连续变量,该条件满足。
条件2:有两个分析因素。本研究有时间因素time和部位因素两个因素,该条件满足。
条件3:观察变量为重复测量数据,即不满足独立性。本研究中在4个时刻测量的蛋白酶活性均是针对同一批样本,因此不满足独立性;相同个体不同部位也不满足独立性;该条件满足。
条件4:观察变量不存在显著的异常值,该条件需要通过软件分析后判断。
条件5:各组、各水平(时刻)观察变量为正态(或近似正态)分布,该条件需要通过软件分析后判断。
关于方差齐性的问题,有无本案例不存在分组因素,因此无须检验方差齐同。
三、软件操作及结果解读
(一) 导入数据
mydata = read.csv("./两重复测量因素方差分析二(有交互作用).csv", header = T)
str(mydata)
结果见图2。

mydata$ID = factor(mydata$ID)
mydata$Site <- factor(mydata$Site, levels = c(1, 2),
labels = c("A部位", "B部位"))
(二) 适用条件判断
1. 条件4判断(异常值判断)
(1) 软件操作
boxplot(mydata$time1 ~ mydata$Site, boxwex = 0.25, col = c('lightblue'),
xlab = '', ylab = '活性', main = 'time = 10 min')
(2) 结果解读
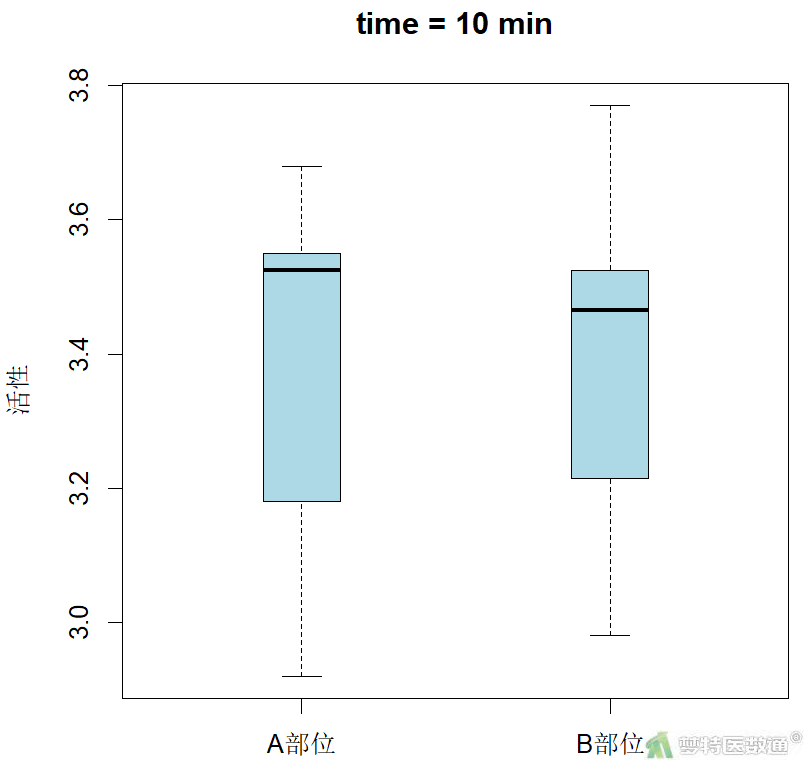
异常值通过箱线图和专业知识进行判断,图3为时刻1时A部位和B部位活性的箱线图,提示不存在异常值。依次可判定其他时刻A、B部位数据也不存在异常值(请读者自行操作)。
2. 条件5判断(正态性检验)
(1) 软件操作
mydata1 = subset(mydata, mydata$Site == "A部位")
mydata2 = subset(mydata, mydata$Site == "B部位")
p1 = p2 = {}
for (i in 1:4) {
p1[i] = shapiro.test(mydata1[, i + 2])[["p.value"]]
p2[i] = shapiro.test(mydata2[, i + 2])[["p.value"]]
}
p1; p2
(2) 结果解读
Shapiro-Wilk (夏皮罗-威尔克,S-W)正态性检验结果(图4)显示,大多数数据的P值均>0.05,提示各时刻两部位的数据整体服从正态分布。关于正态性检验的注意事项详见推文(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。

(三) 统计描述
(1) 软件操作
##宽数据转换为长数据##
library(reshape2) #调用包“reshape2”
mydata_long <- melt(data = mydata, id.vars = c('ID', 'Site'), #保留不变的变量
measure.vars = c('time1', 'time2', 'time3', 'time4'), #想要转换的变量
variable.name = 'time', #转换后的分类变量名
value.name = 'tvalue') #转换后的数值变量名
## 统计描述 ##
library(plyr)
em <- ddply(mydata_long, c("time", "Site"), summarise,
mean = mean(tvalue, na.rm = TRUE),
sd = sd(tvalue, na.rm = TRUE),
n = sum(!is.na(tvalue)),
se = sd/sqrt(n),
lower.CI = t.test(tvalue)[["conf.int"]][1],
upper.CI = t.test(tvalue)[["conf.int"]][2])
em
## 绘制边际均数图 ##
library(ggplot2)
ggplot(em, aes(x = time, y = mean, color = Site, group = Site)) + #绘制分组图
geom_errorbar(aes(ymin = lower.CI, ymax = upper.CI), width = .05)+ #添加误差线
geom_line() + #添加连线
geom_point() #添加点
ggsave("emplot.png", width = 8, height = 5, dpi = 300) #保存图片
(2) 结果解读
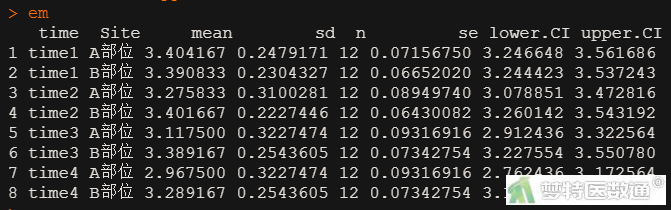
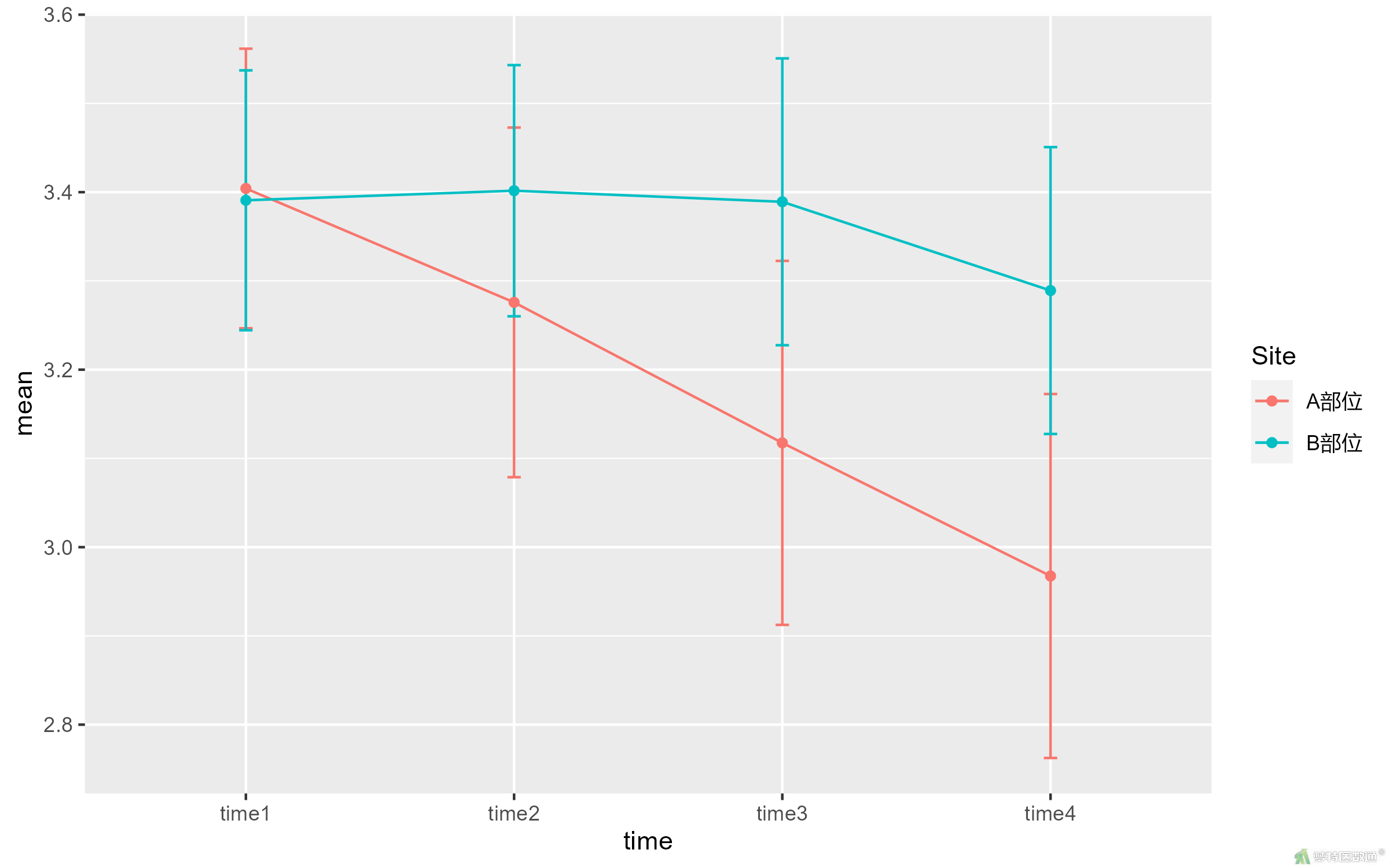
统计描述结果(图5)列出了两部位time1、time2、time3、time4的估算边际平均值、标准误差及均数的95%CI。估算边际均值图(图6)绘制了两部位4个时刻蛋白酶活性的变化情况,可见两组数据均有下降,但下降幅度的趋势有差异。
(四) 球形假设检验及方差分析
(1) 软件操作
library(ez) #调用包“ez”
ezANOVA(data = mydata_long, dv = tvalue, wid = ID,
within = .(time, Site), detailed = T) #重复测量方差分析
(2) 结果解读
“莫奇来球形度检验”结果(图7)给出了球形假设检验结果,可见“时间(time)”、“时间*部位(time*Site)”的检验结果均P<0.05,提示不满足球形假设。
当违背了球形假设条件时,可采用“多变量检验”结果,或者使用单变量检验校正法的结果,包括格林豪斯-盖斯勒、辛-费德特和下线3种校正方法。单变量检验校正法一般建议采用前两种方法,当epsilon (ε)<0.75时,使用格林豪斯-盖斯勒法,当epsilon (ε)>0.75时,使用辛-费德特法。当违背了球形假设条件时,如果单变量和多变量检验结果不一致,以多变量检验结果为准。

(五) 交互作用判断
由于本案例有两个因素(一个为时间,另一个为部位),因此需要首先判断两个因素之间是否存在交互作用。如果交互作用有统计学意义,则需要分析单独效应。
“ANOVA (方差分析)”结果(图7)显示,time与Site之间的交互作用结果为F时间*部位=41.097,P<0.001,提示时间与部位之间交互作用有统计学意义。因此,本案例需要分析单独效应。
(六) 单独效应分析
1. 软件操作
library(bruceR) #调用程序包"bruceR"
library(magrittr) #调用程序包"magrittr"
library(dplyr) #调用程序包"dplyr"
MANOVA(data = mydata_long, subID = "ID",
dv = "tvalue", within = c("time", "Site")) %>%
EMMEANS("time", by = "Site") %>%
EMMEANS("Site", by = "time")

2. 结果解读
(1) 时间的单独效应
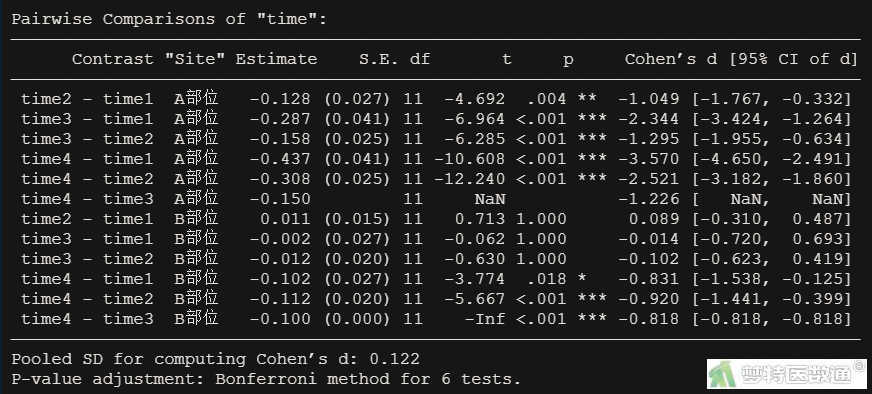
“时间的成对比较”结果(图8)显示,部位1 (部位A)的蛋白酶活性在4个时刻之间两两比较,差异均有统计学意义,即随着时间的延长活性越来越低。
(2) 部位的单独效应
部位的单独效应是指在不同时刻比较不同部位蛋白酶活性差异。“部位的联合检验”结果(图9)显示,time1时,两部位之间的差异无统计学意义(F=0.378,P=0.551);但time2 (P=0.008)、time3(P<0.001)、time4(P<0.001)时,两部位之间的差异均有统计学意义,且结合“部位的成对比较”结果(图9)可知,随着时间的推移,两部位之间的差异越来越大。
四、结论
本研究采用两重复测量因素方差分析评价在麻醉药物的作用下,A、B部位某蛋白酶活性变化情况。数据不存在异常值,整体数据服从正态分布;时间与部位之间存在交互作用(F时间*部位=41.097,P<0.001),故进行单独效应分析。
时间的单独效应分析显示,在部位A,随着时间的延长蛋白酶活性越来越低。部位的单独效应分析显示,time1时,两部位之间的差异无统计学意义(F=0.378,P=0.551);但time2 ((F=10.605,P=0.008)、time3((F=32.827,P<0.001)、time4((F=46.023,P<0.001)时,两部位之间的差异均有统计学意义,且随着时间的推移,两部位之间的差异越来越大。
综上,该麻醉药对A部位的蛋白酶活性影响高于B部位。