单因素协方差分析(One-Way ANCOVA)——SPSS软件实现

关键词：SPSS; 协方差分析; 单因素协方差分析; 平行性检验; 平行线检验

一、案例介绍

为研究A、B、C三种饲料对增加小鼠体重的影响，将初始体重相近的45只小鼠随机分成三组，分别喂养A、B、C三种饲料，但在实验设计时未对小鼠的进食量加以限制，现测得三组小鼠的进食量和所增体重，请推断A、B、C三种饲料对小鼠的增重效果是否有差别？

创建代表喂养饲料种类的变量“group”，1、2、3 三种数字代表“A”、“B”、“C”三种饲料，测量尺度设为“名义”；创建代表“进食量”和“所增体重”的变量“Food”和“Weight”，测量尺度设为“标度”。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较A、B、C三种饲料对增加小鼠体重的影响，即A、B、C三组体重增量是否存在差异。但显然，每个老鼠的进食量会对体重增量产生影响，因此针对这种情况可将进食量作为体重增量的影响因素进行单因素协方差分析(One-Way ANCOVA)。但需要满足9个条件：

条件1：观察变量为连续变量。本研究中观察变量为体重增量，为连续变量，该条件满足。

条件2：自变量为二分类或多分类变量。本研究中自变量为A、B、C三组，该条件满足。

条件3：协变量是连续变量。本研究中协变量为进食量，为连续变量，该条件满足。

条件4：各研究对象之间具有独立的观测值。本研究中各个研究对象均为独立样本，不存在互相干扰的情况，该条件满足。

条件5：观察变量不存在显著异常值，该条件需要通过软件分析后判断。

条件6：各组内协变量和因变量之间存在线性关系，该条件需要通过软件分析后判断。

条件7：各组内因变量的残差服从正态(或近似正态)分布。

条件8：组间因变量的残差方差齐，该条件需要通过软件分析后判断。

条件9：各组内协变量和因变量的回归直线平行，即通过平行性检验，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件6判断(线性关系判断)

为了知晓各组内协变量和因变量之间是否存在线性关系，可通过绘制散点图来实现。

(1) 软件操作

①选择“图形”—“图表构建器” (图2)。

②在“图表构建器”对话框的“图库”中，选择“散点图/点图”，双击选择“分组散点图” (图3)。

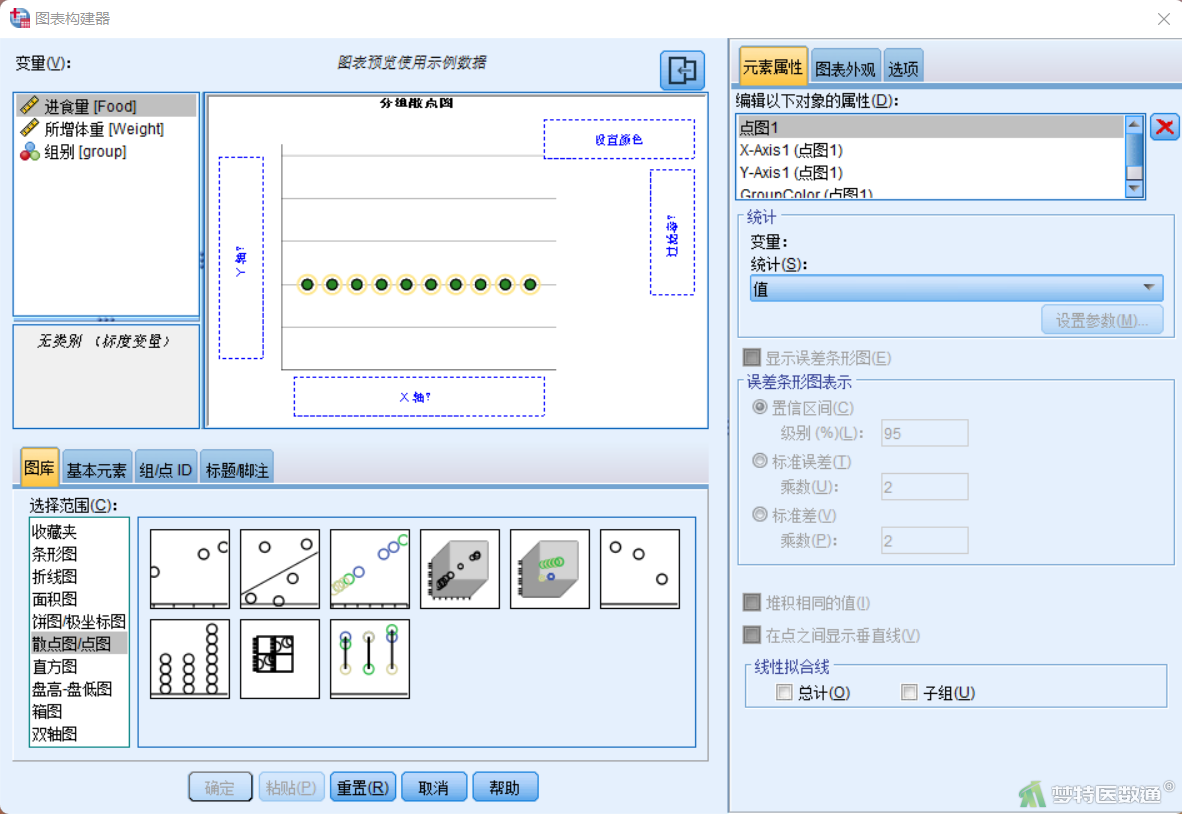
③将观察变量“Food”“Weight”和“group”分别拖拽到“X轴”、“Y轴”和“设置颜色”方框中(图4)。

④点击“确定”，即可得散点图(图5)。

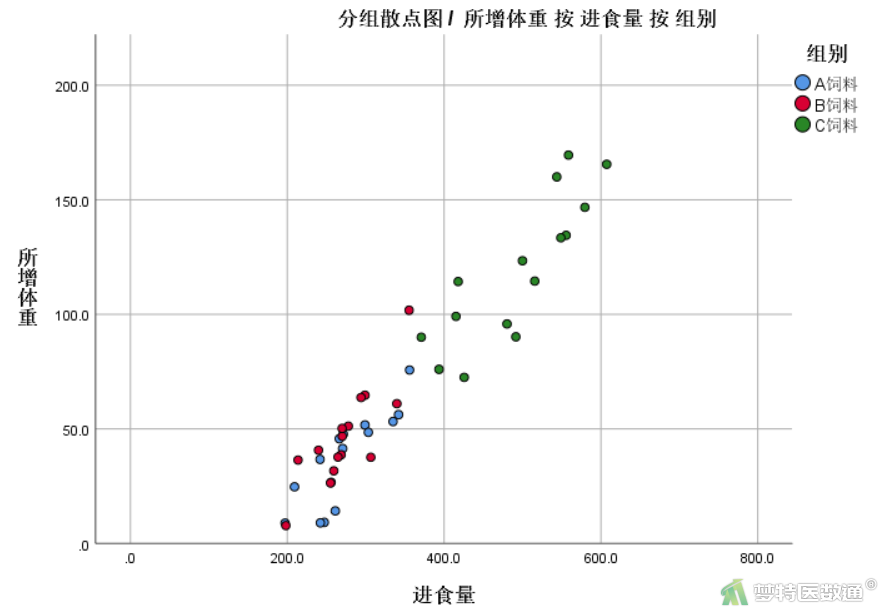
⑥双击散点图，“图表编辑器”对话框，点击“元素”，勾选“子组拟合线”(图6)，即可得散点图拟合趋势线(图7)。

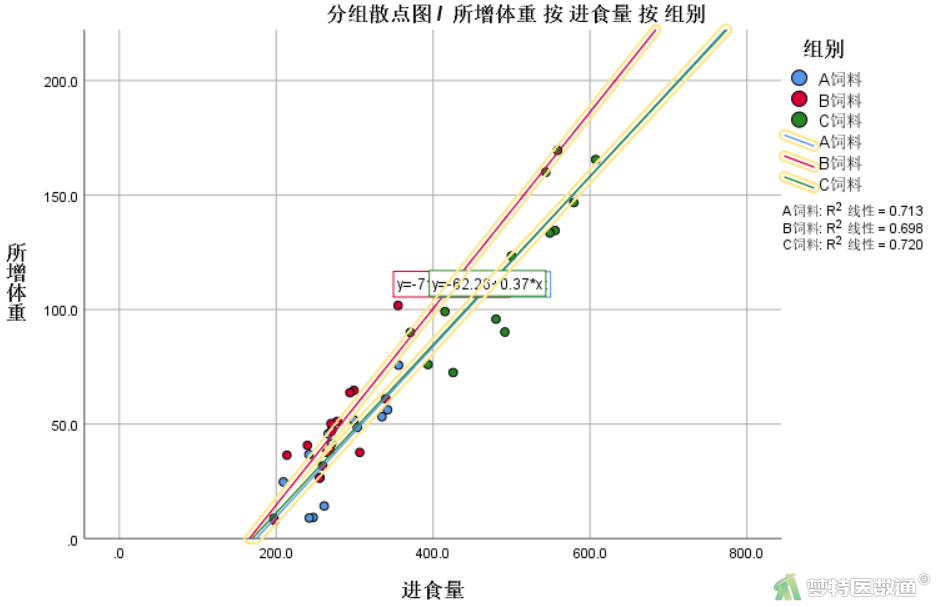
(2) 结果解读

图7是对三组数据拟合曲线的分析结果，从图中可以看出，各组内协变量(Food)和因变量(Weight)存在线性关系，满足条件6。

2. 条件9判断(平行性检验)

检验各组内协变量和因变量的回归直线是否平行，可通过检验回归方程中的自变量与协变量是否存在交互作用加以判断。

(1) 软件操作

①选择“分析”—“一般线性模型”—“单变” (图8)。

②在弹出的对话框中，将观察变量“Weight”选入右侧“因变量”框、将分组变量“group”选入右侧“固定因子”框、将观察变量“Food”选入右侧“协变量”框(图9)。

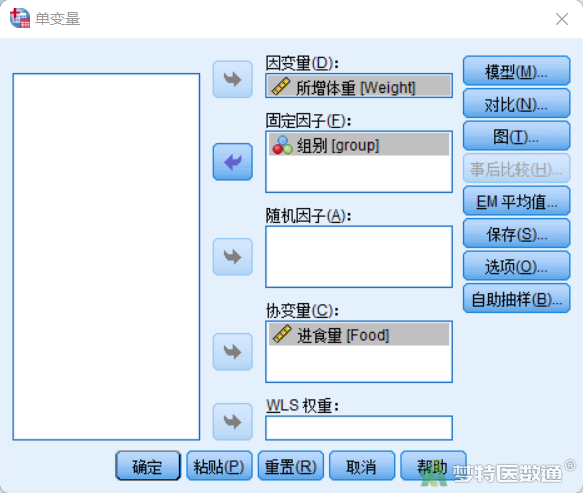
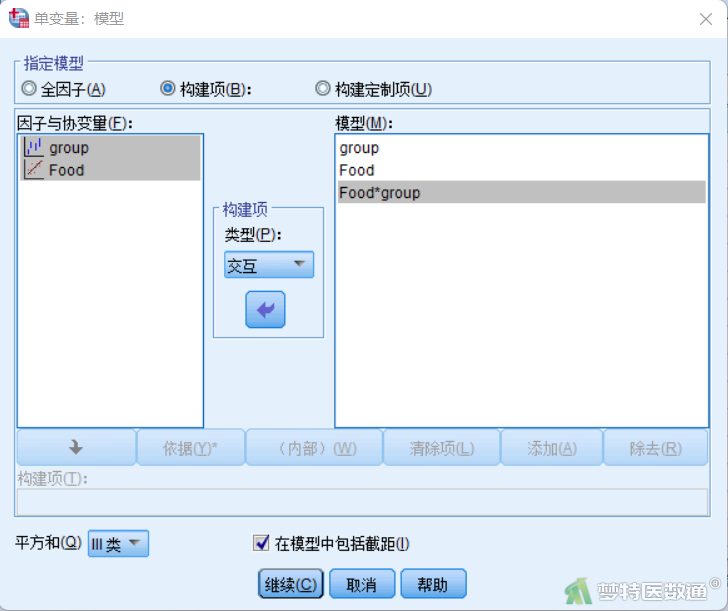
③点击右侧“模型”， 选择“指定模型”中的“构建项”选项，将观察变量“group”和“Food”分别放入“模型”栏，并按住ctrl键同时选择“group”和“Food”变量放入“模型”栏，生成交互项，点击“继续” (图10)，回到“单变量”对话框，点击“确定”。

(2) 结果解读

图11是两组数据主体间效应检验的结果，如果自变量与协变量的交互项具有统计学意义，那么就说明各组间回归斜率不同；若自变量与协变量的交互项没有统计学意义，就说明各组间回归斜率相同。

从图中可见，“修正模型”列的F =81.721，显著性<0.001，表示整体模型检验具有统计学意义。自变量(group)和协变量(Food)交互项的检验结果为F_group*Food =0.186，P_group*Food=0.831，没有统计学意义，说明各组间回归斜率相同，即回归直线平行。因此，本案例满足条件9。

3.条件8判断(方差齐性检验)

我们可通过生成预测值(PRE_1)和标准化残差(ZRE_1)变量来进行正态性检验、方差齐性检验和异常值判断。

(1) 软件操作

①步骤同条件9判断，选择“分析”—“一般线性模型”—“单变量” (图8)。

②在弹出的对话框中，将观察变量“Weight”选入右侧“因变量”框、将分组变量“group”选入右侧“固定因子”框、将观察变量“Food”选入右侧“协变量”框(图9)。

③点击右侧“模型”，选择“指定模型” 中的“全因子”选项，点击“继续”，回到“单变量”对话框(图12)。

④点击右侧“保存”，在弹出的对话框中，选择“预测值”中的“未标准化”选项，选择“残差”中的“标准化”选项，点击“继续” (图13)，回到“单变量”对话框。

⑤点击右侧“选项”，在弹出的对话框中，在“选项”栏内，勾选描述统计、效应量估算和齐性检验(图14)。点击继续，回到“单变量”对话框，点击“确定”按钮。

(2) 结果解读

图15显示为模型的非标准化预测值(PRE_1)和标准化残差(ZRE_1)变量。

图16显示为方差齐性检验结果。从图中可以看出，误差方差的莱文等同性检验的F=2.063，显著性=0.140，说明各组间因变量的残差方差齐，满足条件8。

4. 条件7 (正态性检验)

(1) 软件操作

①选择“分析”—“描述统计”—“探索”(图17)。

②在“探索”对话框中将观察变量 “ZRE_1”选入右侧“因变量列表”框(图18)。

③点击右侧“图”，在子对话框中勾选“带检验的正态图”和 “茎叶图”，其他不变(图19)。

④点击“继续”，回到“探索”对话框，点击“确定”，即可得到正态性检验结果。

(2) 结果解读

经上述操作，SPSS输出了标准化残差的柯尔莫哥洛夫-斯米诺夫，K-S检验和夏皮罗-威尔克正态性，S-W检验结果和Q-Q图。K-S检验适用于大样本资料，本案查看S-W检验结果，图20中P值为0.682，提示数据的标准化残差服从正态分布。

图21为数据的Q-Q图，散点基本围绕对角线分布，提示标准化残差呈正态分布。综上，本案例满足条件7。

5. 条件5 (异常值判断)

(1) 方法一：通过箱式图来判断异常值

①软件操作

选择“分析”—“描述统计”—“探索”(图17)。

在“探索”对话框中将观察变量 “ZRE_1”选入右侧“因变量列表”框、将分组变量“group”选入右侧“因子列表”框(图22)。

点击右侧“图”，在子对话框中勾选“带检验的正态图”和“茎叶图”，其他不变(图19)。

点击“继续”，回到“探索”对话框，点击“确定”，即可得到正态性检验结果。

②结果解读

图23是三种饲料喂养下小鼠所增体重标准化残差的箱式图，结果显示无异常值，因此本案例未发现需要删除的异常值，满足条件5。

(2) 方法二：借助标准化残差(ZRE_1)变量的排序判断异常值

① 软件操作

在数据视图中，右击ZRE_1数据栏，选择“升序排序”(图24)。

将标准化残差(ZRE_1)升序排列后，可在数据栏的最上方和最下方检查是否存在大于3或小于-3的离群值。

② 结果解读

图25为排序后的结果，可见模型的标准化残差(ZRE_1)绝对值均不大于3，表明没有异常值，满足条件5。

(二) 统计描述及判断

1. 软件操作

单因素协方差分析的步骤同条件9判断的步骤。因条件9中自变量(group)和协变量(Food)交互项无统计学意义，所以交互项不应放在模型中。

①选择“分析”—“一般线性模型”—“单变量”(图8)。

②在弹出的对话框中，将观察变量“Weight”选入右侧“因变量”框、将分组变量“group”选入右侧“固定因子”框、将观察变量“Food”选入右侧“协变量”框(图9)。

③点击右侧“模型”，在“模型”对话框中，选择“指定模型”中的“构建项”选项，将右侧模型框中“group*Food”移除，只保留“group”和“Food” (图26)。点击“继续”，回到“单变量”对话框，点击“确定”。

④点击右侧“Em边际均值”，将“group”选入右侧“显示下列各项的平均值”框，勾选“比较主效应”，选择“邦弗罗尼法”选项(此步骤将进行多组间的两两比较，如果实际研究中只有两组，则不用选择) (图27)。在“选项”栏内，去掉“齐性检验”的勾选。

⑤点击“继续”，回到“单变量”对话框，点击“确定”按钮。

2. 结果解读

(1) 统计描述

由图28可知，A、B、C三组体重增量分别为36.63±20.37、46.43±21.39、119.03±31.94 g。三组数值存在差异，但由于研究对象的进食量不尽相同，仅从下图中结果很难确定各组饲料喂食的效果，还需要依据协方差分析结果进行判断。

(2) 统计学推断

协方差分析的目的是控制协变量之后分析不同组之间的差别，图29为单因素协方差分析中“主体间效应检验”结果。如图所示，Food这一栏的F_Food=100.524，P_Food<0.001，提示“进食量水平(即协变量Food)”的确对“所增体重(Weight)”具有影响。group这一栏的F_group=1.999，P_group=0.149，提示三组小鼠“所增体重(Weight)” 差异无统计学意义。

在“估算值”中，输出了各组调整“进食量水平(即协变量Food)”后的“所增体重(Weight)”水平。A、B、C三组体重增量分别为64.65±4.50、74.09±4.48、63.35±6.58 g(图30)。

图31为“成对比较”的结果，本案例中由于三组间整体比较差异无统计学意义，因此无需再进行两两比较。如果三组间整体比较差异有统计学意义，则需根据“成对比较”中的结果来具体分析哪两组之间有统计学差异。

四、结论

本研究采用单因素协方差分析，判断在调整进食量后A、B、C三种饲料对小白鼠的增重效果是否有差别。通过绘制散点图，提示各组内协变量和因变量之间存在线性关系；通过平行性检验，发现“group*Food”的交互项无统计学意义(F_group*Food =0.186，P_group*Food=0.831)，提示满足平行性检验要求。通过方差齐性检验提示各组因变量残差满足方差齐性要求。通过标准化残差(ZRE_1)检验正态性和异常值，提示因变量残差满足正态性要求，无需要处理的异常值。

A、B、C三组小白鼠体重增量分别为36.63±20.37、46.43±21.39、119.03±31.94 g。单因素协方差分析显示，在调整进食量后A、B、C三组体重增量的估算边际均值分别为64.65 (95%CI: 55.55~73.75)、74.09 (95%CI: 65.04~83.14)、63.35 (95%CI: 50.05~76.64) g，差异无统计学意义(F_group=1.999，P_group=0.149)。本研究结果提示A、B、C三种饲料对小白鼠体重的增重效果无差异。

五、知识小贴士

• 协方差分析是针对在实验设计阶段难以控制其取值水平，或者无法严格控制的因素，在统计分析阶段对其进行统计控制的一种分析方法，实质为线性回归分析和方差分析的结合。适用于完全随机设计、随机区组(配伍)设计、拉丁方设计、析因设计等类型的方差分析。
• 协方差分析一般要求协变量在组间的观察范围相差不宜太大(分析前最好先对协变量均数间的差别作假设检验)，否则修正后的边际均值的差值可能会落在回归线的延长线上，回归线外推后，是否仍然满足平行线和线性关系尚不可知，其协方差分析的结论可能不一定准确。

六、分析小技巧

• 正态性检验：对协方差分析的正态性条件考察应检验因变量残差的正态性，此时检验多组整体残差的正态性即可，无须检验每组残差的正态性。关于正态性检验的注意事项详见文章(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。
• 方差齐性检验：对协方差分析的方差齐性条件考察应检验组间因变量残差是否相等。关于方差齐性检验的更多内容请阅读(医学统计学核心概念及重要假设检验的软件实现(4/4)——方差齐性检验及SPSS实现)。