单因素计量资料的广义估计方程(Generalized Estimating Equations,GEE)——SPSS软件实现

关键词：SPSS; 重复测量; 重复测量资料; 单因素计量资料; 广义估计方程; GEE; 交互作用; 主效应; 单独效应

一、案例介绍

使用单因素重复测量方差分析(One-Way Repeated Measures ANOVA)——SPSS软件实现一文案例。检验科研究血样放置时间对某生化指标浓度检测的影响，采集了10份人体血液标本，分别在放置0 min(T₀)、30 min(T₃₀)、60 min(T₆₀)和90 min(T₉₀)时对该指标的浓度(mmol/L)进行检测，分析放置时间是否对该生化指标检测结果有影响？

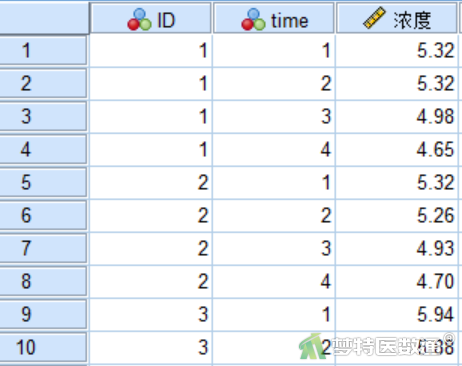
广义估计方程需要使用长型格式数据，部分数据见图1所示。“ID”为血标本编号，time是测量的不同时点T₀、T₃₀、T₆₀和T₉₀，浓度为相应时间点测的的生化指标浓度。本案例数据可从“附件下载”处下载。若数据为宽型格式，需要将其转换为长型格式，具体操作见长宽型数据转换。

二、问题分析

本案例的分析目的是比较4个时间点的生化指标浓度是否有差异。由于4个时间点的数据属于重复测量数据，可以使用广义估计方程进行数据分析。

三、软件操作及结果解读

(一) 软件操作

【模块调取】选择“分析”—“广义线性模型”—“广义估算方程”(图2)

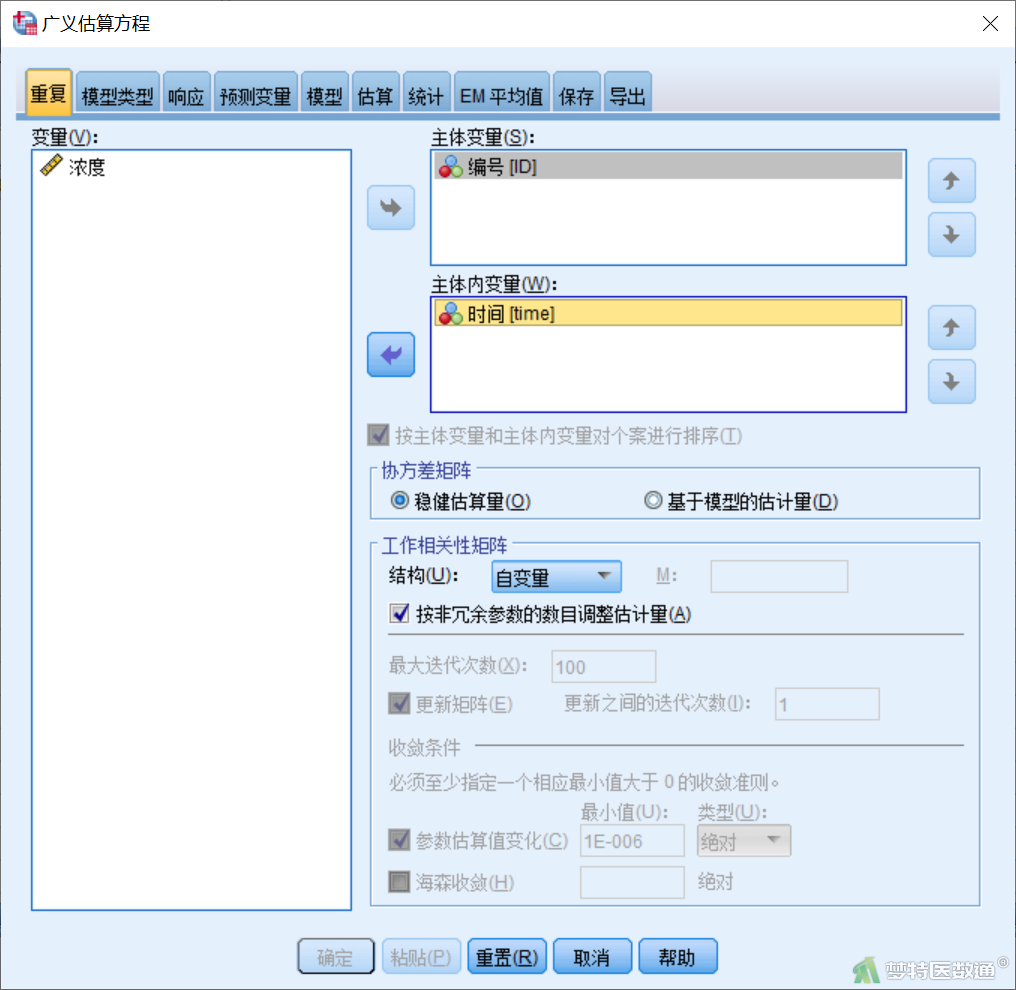
【“重复”模块设置】在“广义估算方程”对话框“重复”模块(图3)中，将识别个体的变量“ID”选入右侧“主体变量”，将表示重复测量的变量“时间”选入“主体内变量”，“工作相关性矩阵”选择默认“自变量(正确翻译为：独立无相关)”，勾选“按非冗余参数的数目调整估计量”。

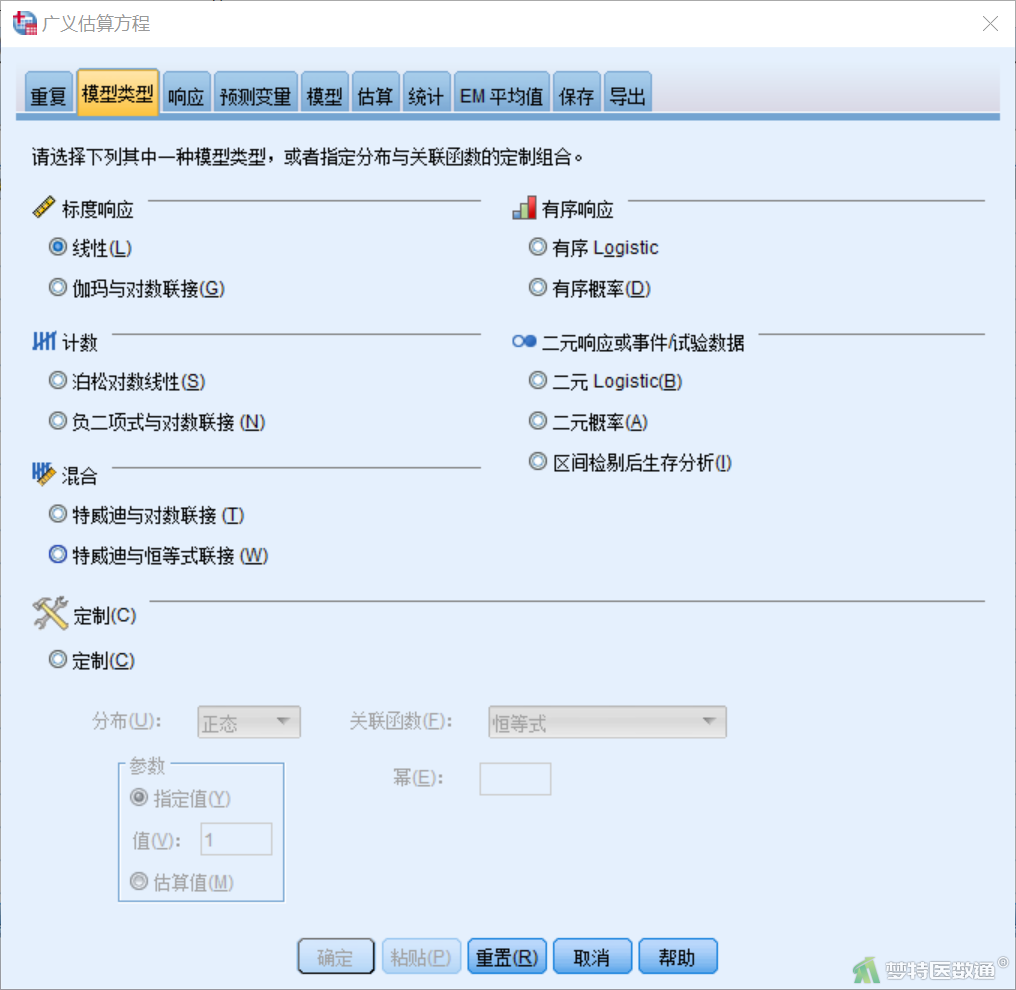
【“模型类型”模块设置】在“广义估算方程”对话框“模型类型”模块(图4)中，因为因变量是计量资料，所以选择“标度响应”下的“线性”。

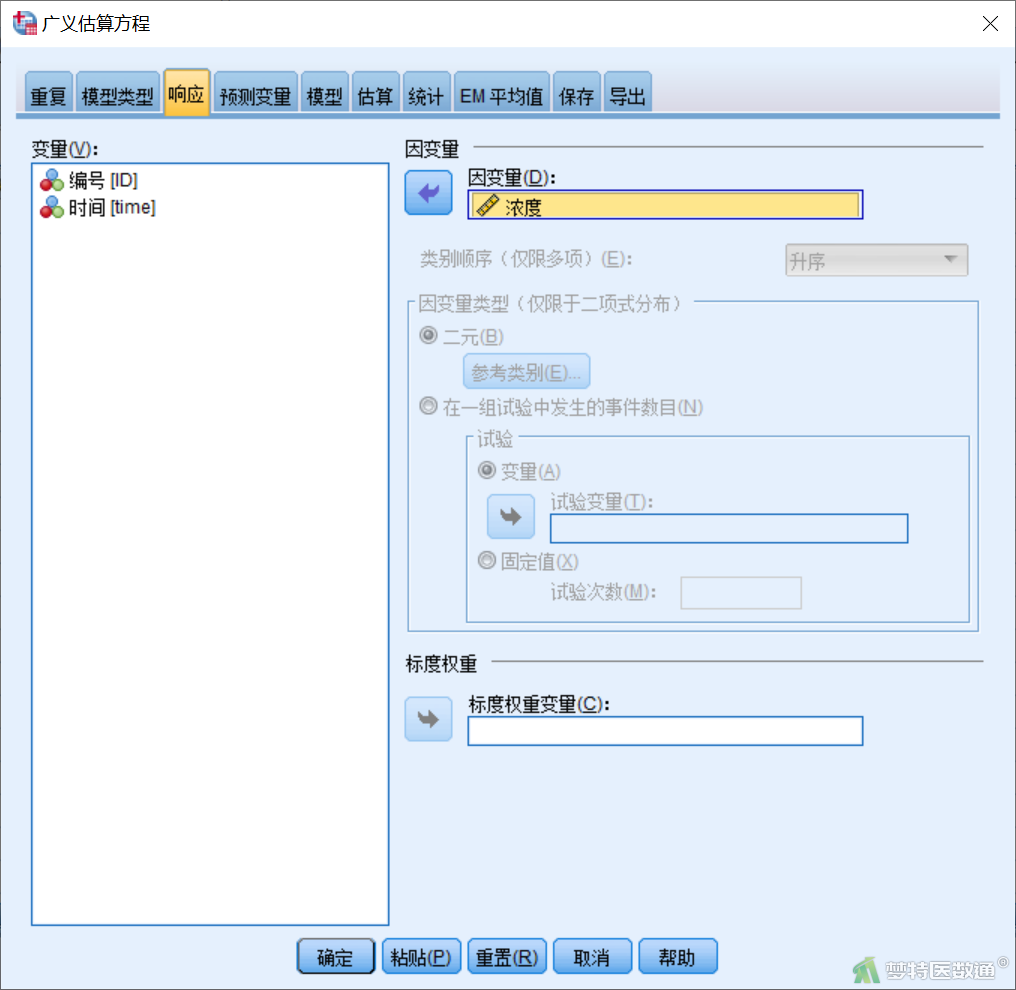
【“响应”(因变量)模块设置】在“广义估算方程”对话框“响应”模块(图5)中，将“浓度”选入“因变量”。

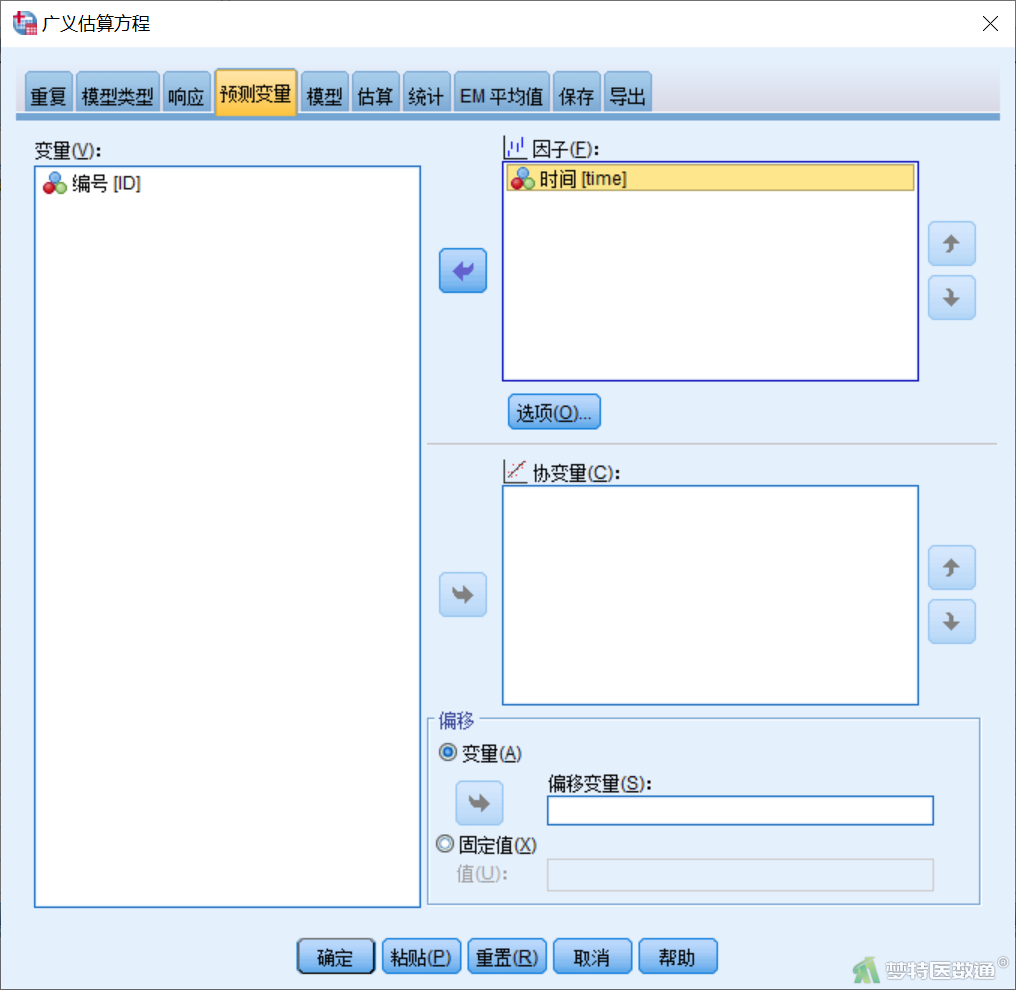
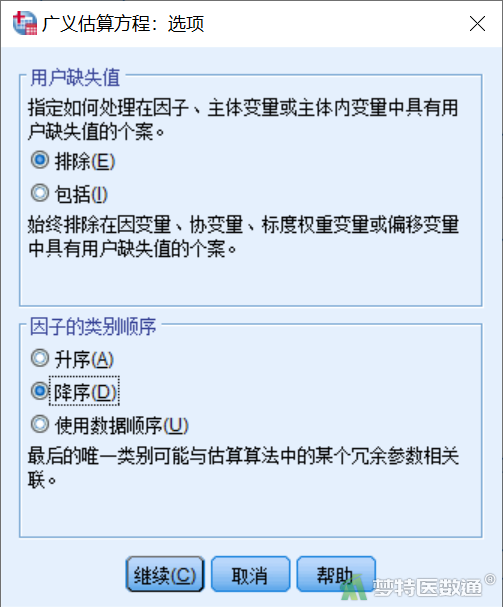
【“预测变量”(自变量)模块设置】在“广义估算方程”对话框“预测变量”模块(图6)中，将“时间”选入“因子”。点击“选项”，打开“选项”子对话框(图7)，“因子的类别顺序”下选择“降序”，表示以自变量的第一个水平为参照计算相关参数和效应量；如果选择“升序”，则是以自变量的最后一个水平为参照计算相关参数和效应量。

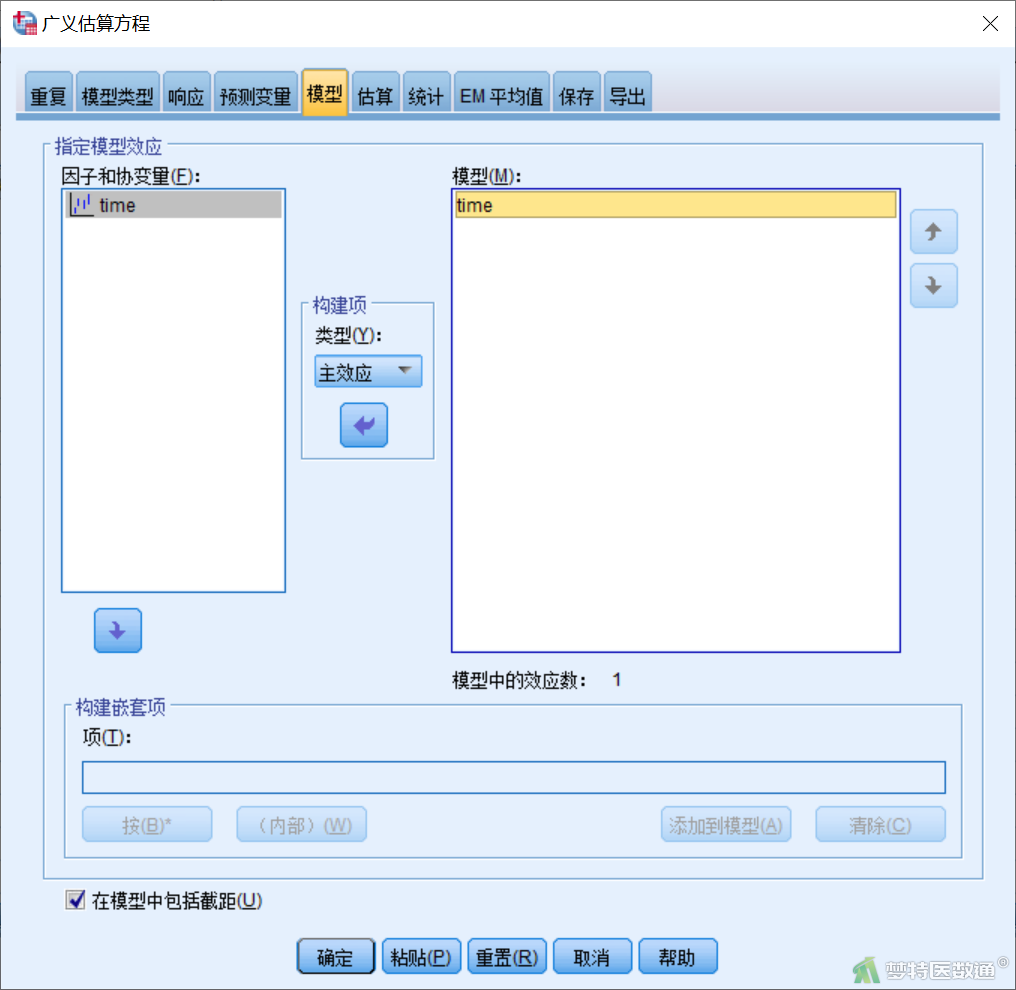
【“模型”模块设置】在“广义估算方程”对话框“模型”模块(图8)中，将time的主效应项选入右侧“模型”。

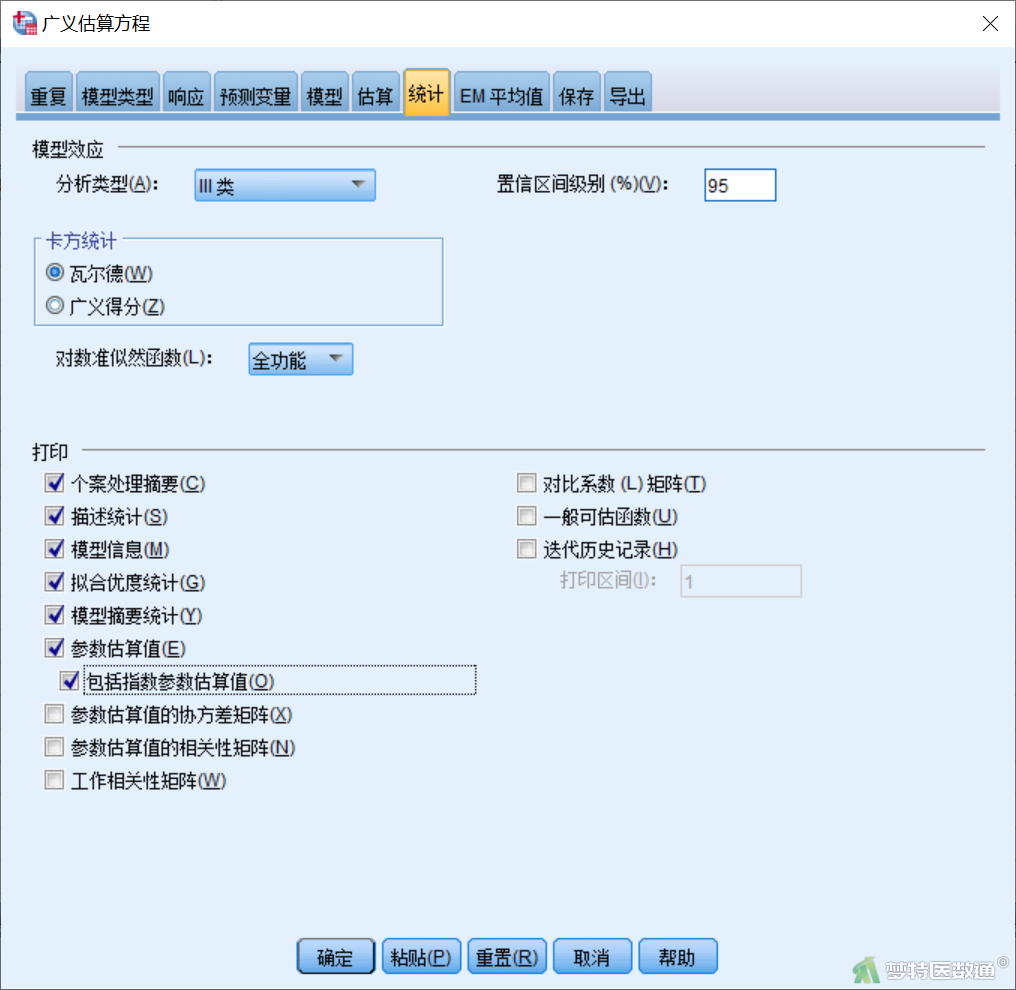
【“统计”模块设置】在“广义估算方程”对话框“统计”模块(图9)中，补充勾选“包括指数参数估算值”，可计算OR、RR等效应量(图9)。

【“EM平均值”(边际估算均值)模块设置】在“广义估算方程”对话框“EM平均值”模块(图10)中，将左侧“因子和交互”下的“time”选入右侧“显示下列各项的平均值”，在“对比”下选择“成对”，左下角“多重比较调整”下选择“邦弗伦尼”。

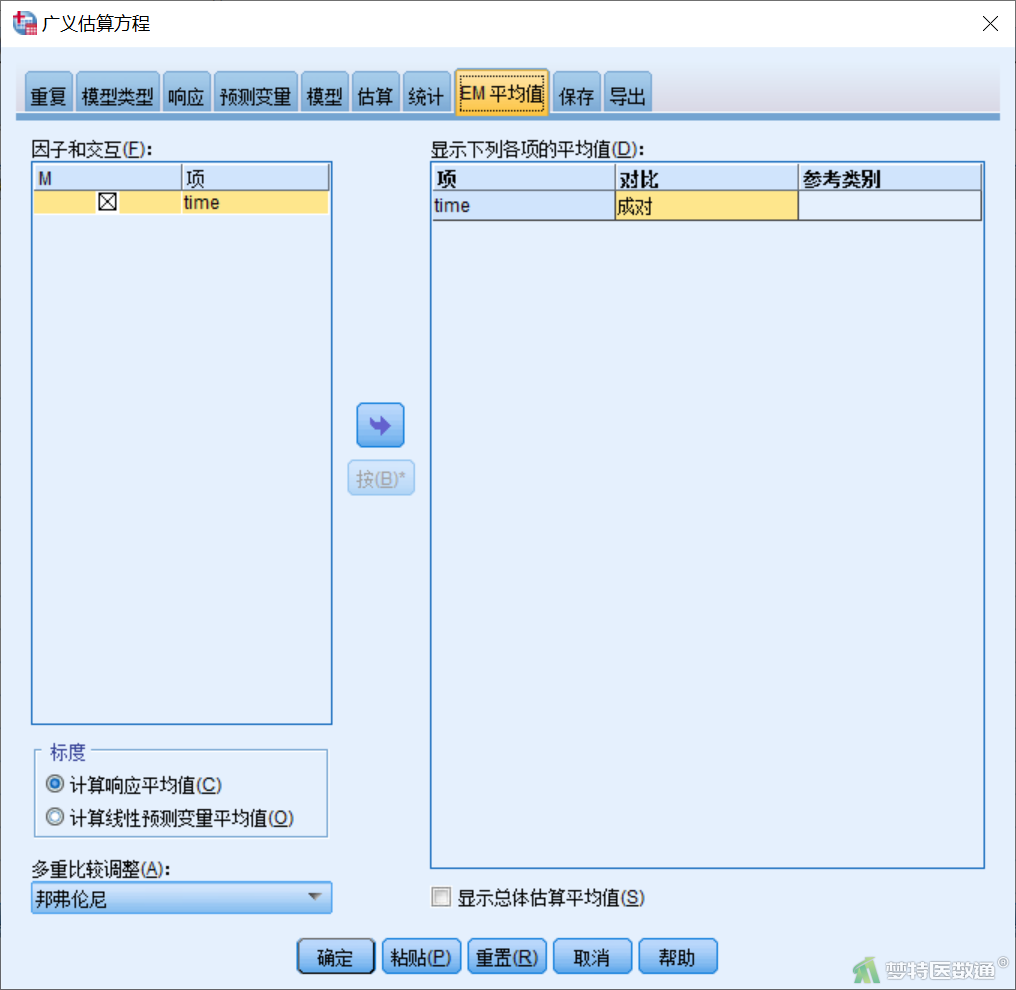
所有模块设置完成后，点击主对话框的“确定”即可。

(二) 结果解读

1. 统计描述

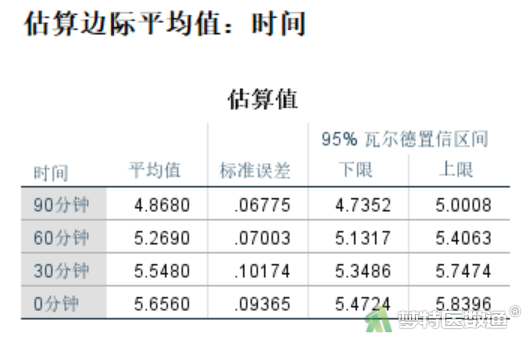
统计描述结果见图11，提供了各组的估算边际均值、标准误差及均值的95%置信区间。因为不存在协变量，所以估算边际均值实际数据均值完全一致。

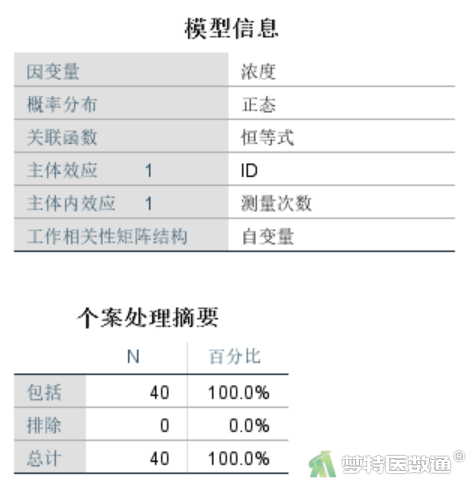
2. 模型摘要

“模型信息”结果(图12)显示，本次分析关联函数为“恒等式”，工作相关性矩阵结构为“自变量(正确翻译为：独立无相关)”。

3. 模型拟合评价

“拟合优度”结果(图13)提供了QIC值和QICC值，表示模型的拟合优度，越小越好，可用于不同作业相关矩阵的分析结果比较。

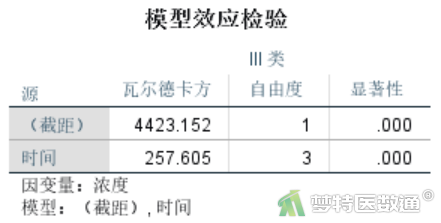
“模型效应检验”结果(图14)提示“时间”的wald χ²=257.605，P<0.001，有统计学意义，表示不同测量时间点的生化指标浓度不同。

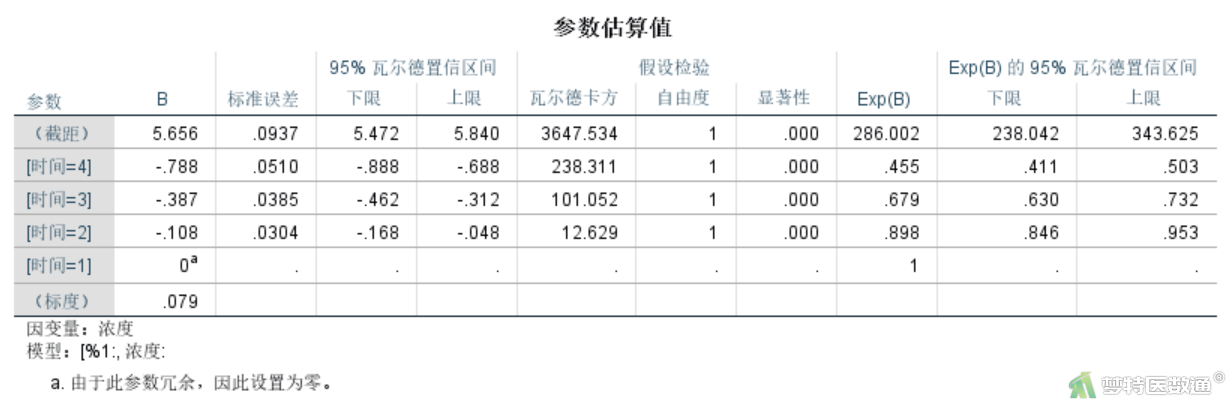
4. 参数估计

“参数估计”结果(图15)列出了各次测量与第一次测量相比的系数及统计学推断结果，可见各个时间点与第一次测量相比差异均有统计学意义(P<0.001)。如T₃₀检测结果比T₀低0.108，T₆₀检测结果比T₀低0.387，T₉₀检测结果比T₀低0.788。

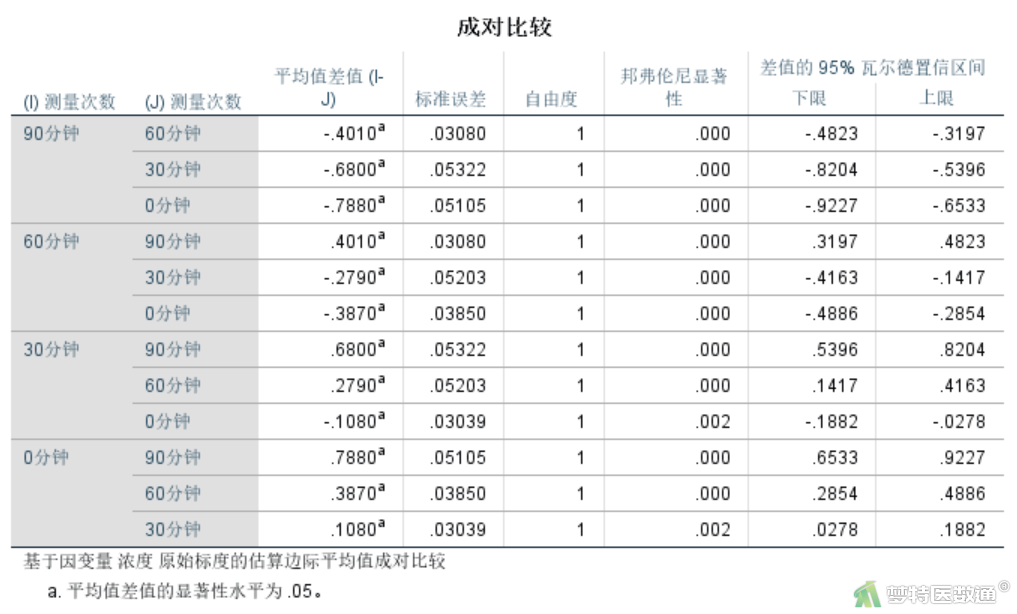
5. 两两比较

“成对比较”结果(图16)提供了各时间点两两比较的“平均值差值”“标准误差”“显著性(校正P值)”和“差值的95%置信区间”。可知，随着时间的延长，各时刻与T₀时刻相比，均数差逐渐增大，且均有统计学意义(P<0.05)。

四、结论

本研究采用广义估计方程分析判断4个时间点的生化指标浓度是否有差异。结果显示，不同测量时间点的生化指标浓度差异有统计学意义(P<0.001)。各个时间点与第一次测量相比差异均有统计学意义(P<0.001)，随着放置时间越长，生化指标浓度越低。T₃₀检测结果比T₀低0.108，T₆₀检测结果比T₀低0.387，T₉₀检测结果比T₀低0.788。

综上可知，放置时间对该生化指标检测结果具有较大的影响。本例分析结果和单因素重复测量方差分析(One-Way Repeated Measures ANOVA)——SPSS软件实现一致。