在重复测量数据方差分析过程中,如果存在协变量,需要使用重复测量协方差分析的方法处理数据。这种情况常见于重复测量数据中包含基线测量数值的情况。同样,在广义估计方程(generalized estimatingequations, GEE)中同样可以处理带协变量的数据。本文将实例演示在SPSS软件中通过GEE分析代谢变量的重复测量数据(无交互作用)的操作步骤。
关键词:SPSS; 重复测量; 重复测量资料; 协变量; 交互作用; 主效应; 单独效应; 协方差分析; 基线数据
一、案例介绍
使用两因素重复测量协方差分析一(无交互作用)—SPSS软件实现一文案例。研究A、B两种饲料对家兔的增重效果,选择20只家兔,随机分成两组,第一组用饲料A饲养,第二组用饲料B饲养,并于实验开始时(time0)、试验开始后第一个月(time1)、第二个月(time2)、第三个月(time3)分别测量2组家兔体重,试比较A、B两种饲料对家兔的增重效果有无差别?
广义估计方程需要使用长型格式数据,部分数据见图1。ID为研究对象编号,group是分组(1=A饲料,2=B饲料);time0是实验开始时的测量体重,time是不同时点(time1、time2、time3)的测量次数;weight为相应时间点检测的体重。本案例数据可从“附件下载”处下载。若数据为宽型格式数据,需要将其转换为长型格式,具体操作见长宽型数据转换,注意在转换过程中time0的数据不要被转成为长型格式。

二、问题分析
重复测量数据分析往往会遇到基线数据和后续测量数据的条件不一致的情况,如针对某种治疗方法对镇痛效果的影响,测量了治疗前和治疗后多次时间点的镇痛效果,此时基线数据和后续多个测量数据的条件则不一致。对于这种情况,基线数据一般不应作为重复测量的第一次纳入重复测量方差分析。本案例也是如此,其中试验开始时的测量数据与后面3次测量数据并不处于同一试验条件下,不适合当做重复测量数据进行分析,而应该当做协变量进行处理。
本案例的分析目的是比较A、B两种饲料对家兔的增重效果有无差别。由于3个时间点的数据属于重复测量数据,且有两个组别,一个协变量,可以使用广义估计方程进行数据分析。
三、软件操作及结果解读
(一) 软件操作
【模块调取】选择“分析”—“广义线性模型”—“广义估算方程”(图2)。
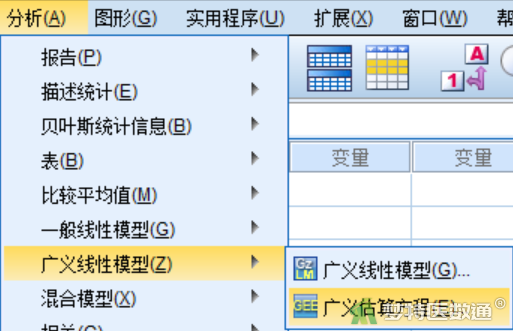
【“重复”模块设置】在“广义估算方程”对话框“重复”模块(图3)中,将识别个体的变量“ID”选入右侧“主体变量”,将表示重复测量的变量“时间”选入“主体内变量”,“工作相关性矩阵”选择默认“自变量(正确翻译为:独立无相关)”,勾选“按非冗余参数的数目调整估计量”。
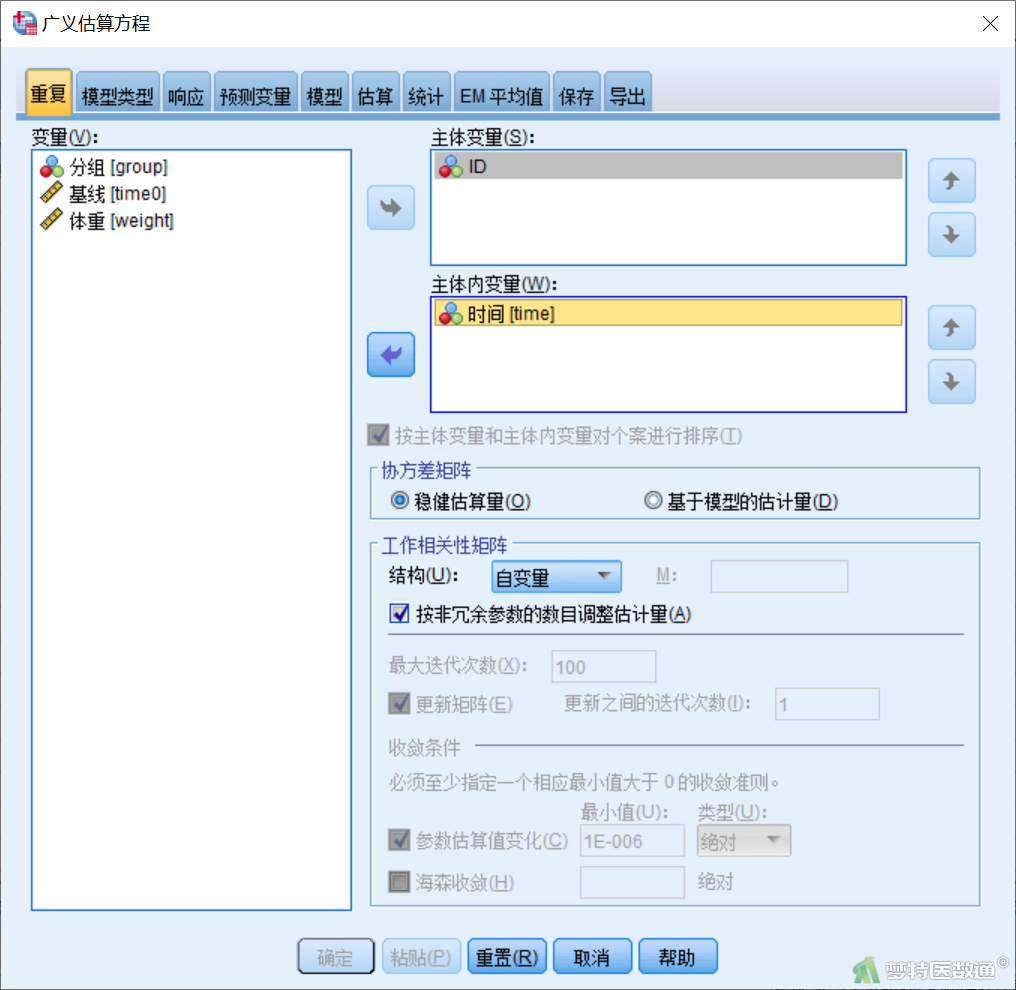
【“模型类型”模块设置】在“广义估算方程”对话框“模型类型”模块(图4)中,因为因变量是计量资料,所以选择“标度响应”下的“线性”。
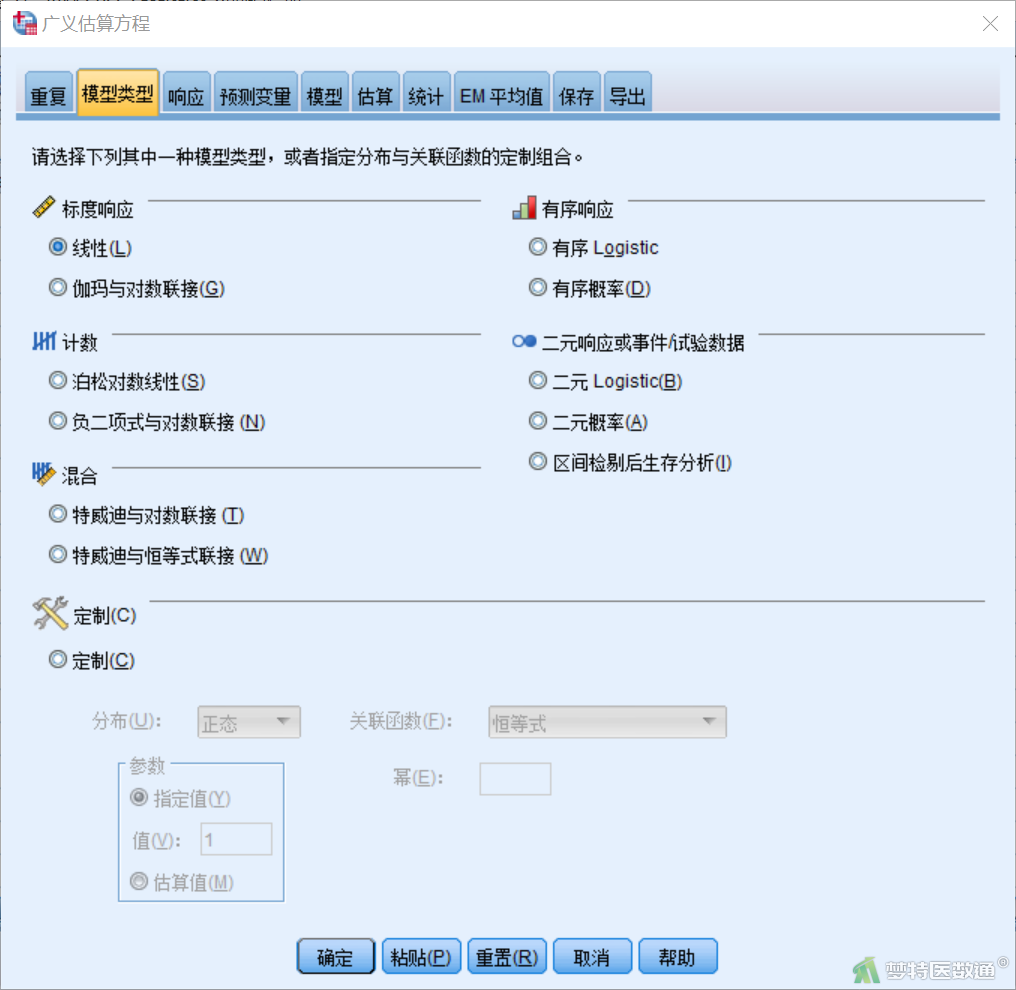
【“响应”(因变量)模块设置】在“广义估算方程”对话框“响应”模块(图5)中,将“体重”选入“因变量”。
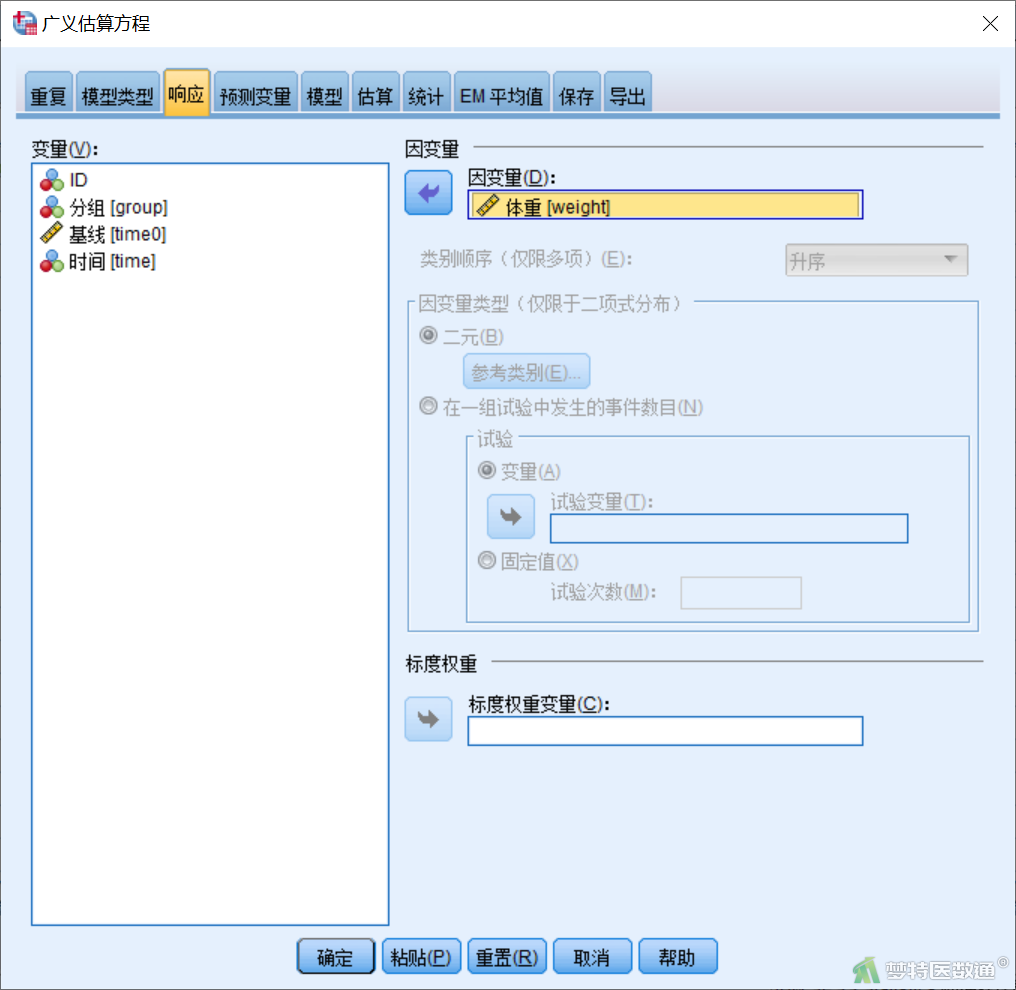
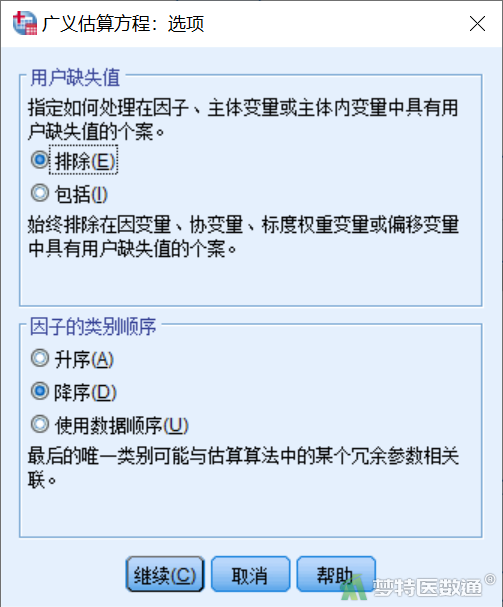
【“预测变量”(自变量)模块设置】在“广义估算方程”对话框“预测变量”模块(图6)中,将“分组”和“时间”选入“因子”。点击“选项”,打开“选项”子对话框(图7),“因子的类别顺序”下选择“降序”,表示以自变量的第一个水平为参照计算相关参数和效应量;如果选择“升序”,则是以自变量的最后一个水平为参照计算相关参数和效应量。
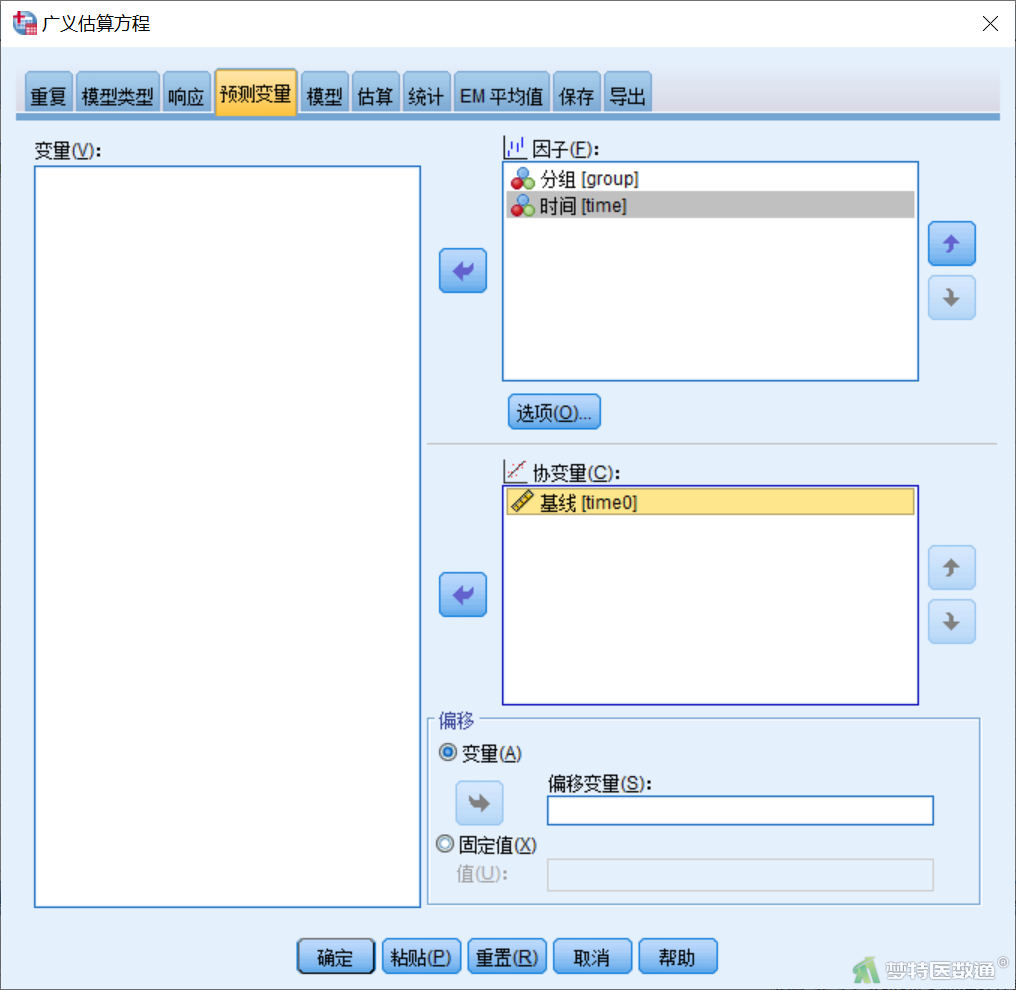
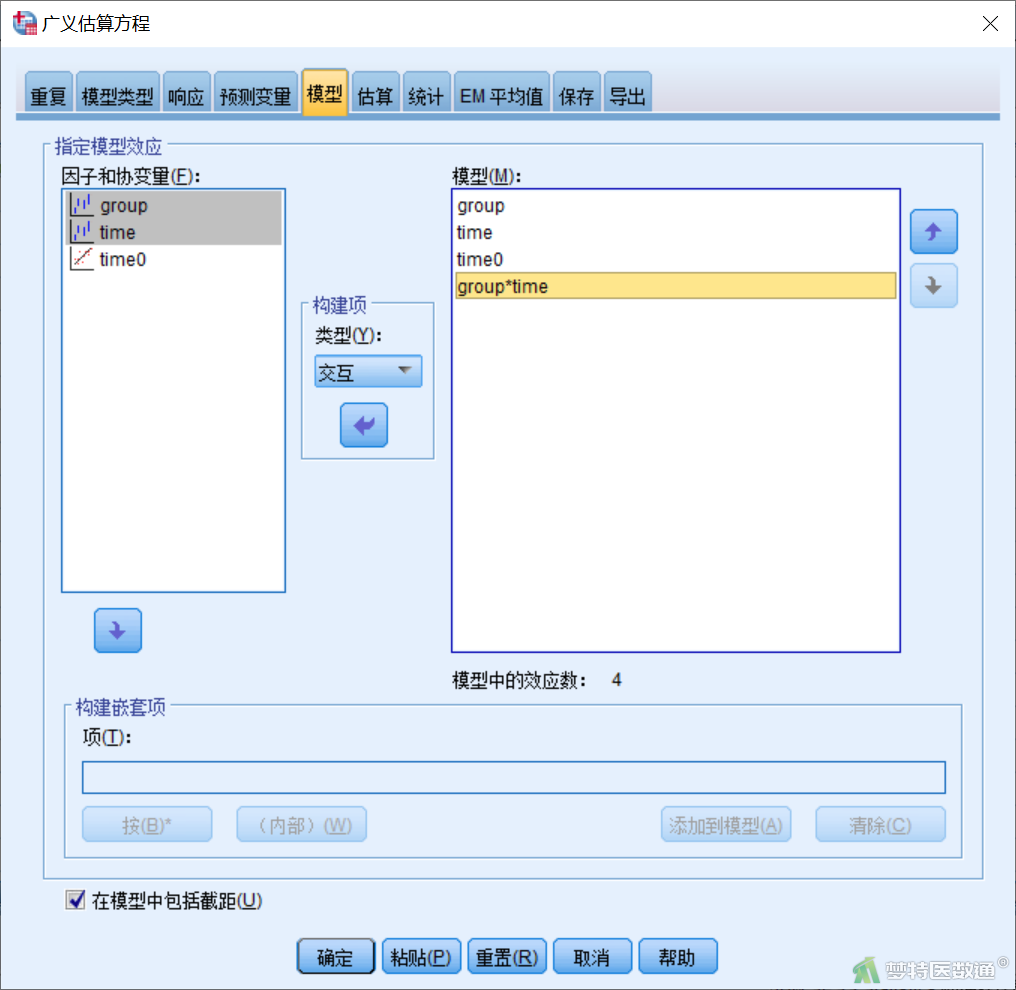
【“模型”模块设置】在“广义估算方程”对话框“模型”模块(图8)中,将group、time、time0的主效应项以及group*time的交互效应项选入右侧“模型”。
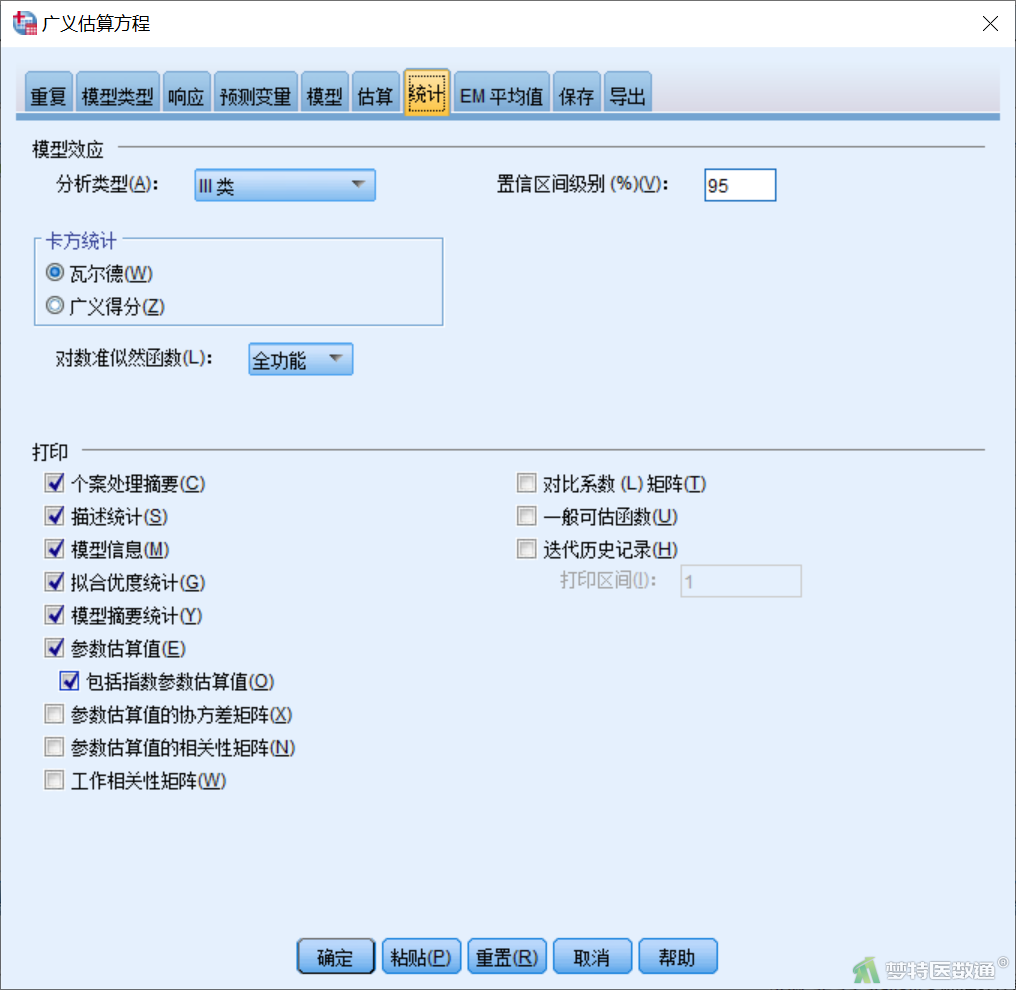
【“统计”模块设置】在“广义估算方程”对话框“统计”模块(图9)中,补充勾选“包括指数参数估算值”,可计算OR、RR等效应量。
【“EM平均值”(边际估算均值)模块设置】在“广义估算方程”对话框“EM平均值”模块(图10)中,将左侧“因子和交互”下的group、time、group*time选入右侧“显示下列各项的平均值”,在“对比”下选择“成对”,左下角“多重比较调整”下选择“邦弗伦尼”。
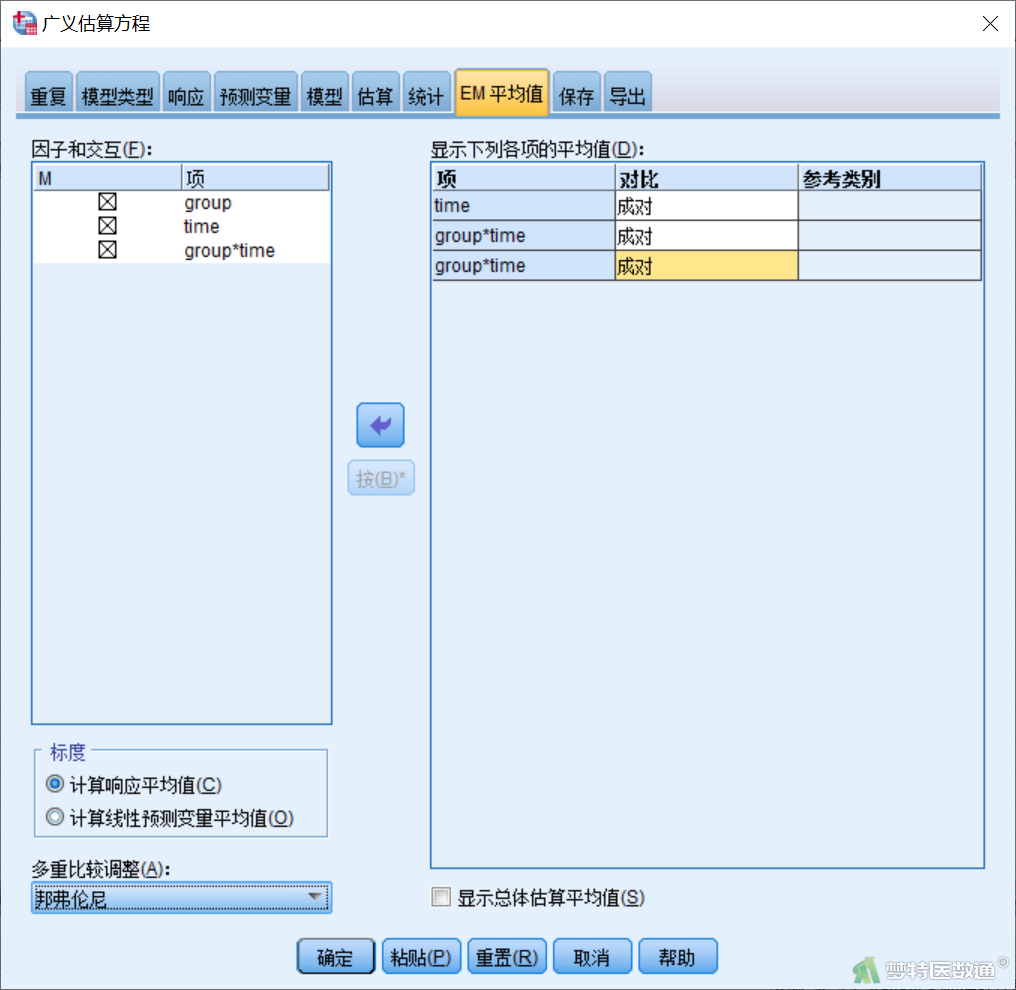
所有模块设置完成后,点击主对话框的“确定”即可。
(二) 交互效应判断
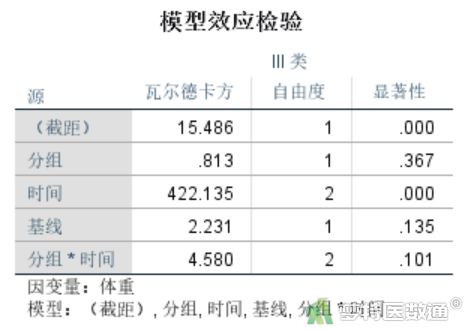
模型效应检验结果(图11)显示,“分组*时间”之间的交互效应无统计学意义(P=0.101),因此在“模型”模块设置(图8)中将“group*time”的交互效应项移除“模型框”,然后重新分析数据。下面展示重新分析后的结果。
(三) 主效应分析
1. 统计学描述
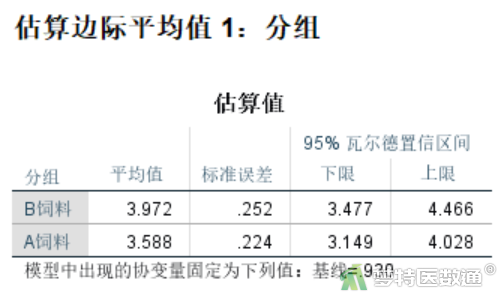
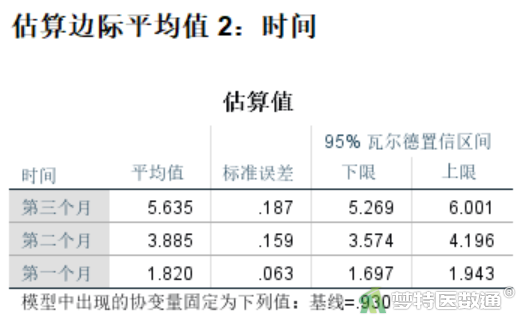
统计描述结果见图12~13,分别提供了按饲料分组和按时间分组的各组各组估算边际平均值、标准误差及均数的95%置信区间。因为对协变量(基线体重)进行了校正,所以估算边际平均值与实际数据均数并不相同。
2. 模型摘要
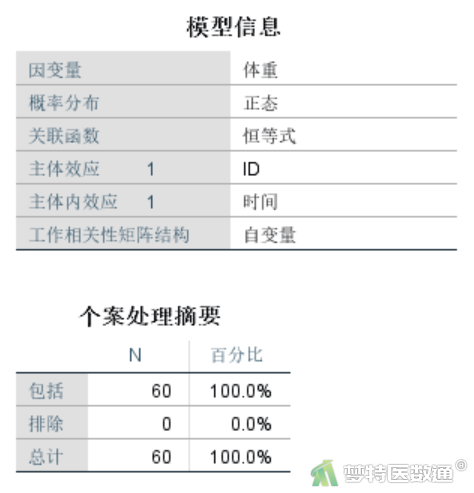
“模型信息”结果(图14)显示,本次分析关联函数为“恒等式”,工作相关性矩阵结构为“自变量(正确翻译为:独立无相关)”
3. 模型拟合评价
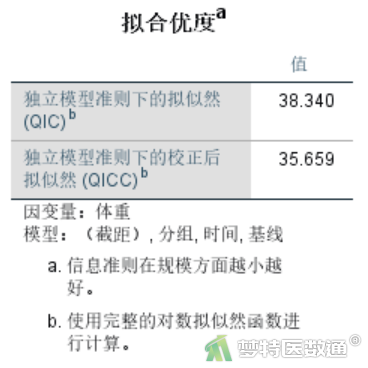
“拟合优度”结果(图15)提供了QIC值和QICC值,表示模型的拟合优度,越小越好,可用于不同作业相关矩阵的分析结果比较。此处可与保留“group*time”交互项的模型比较,发现去掉交互项后QIC值和QICC值均降低,也表明去掉交互项后模型拟合得到进一步优化。
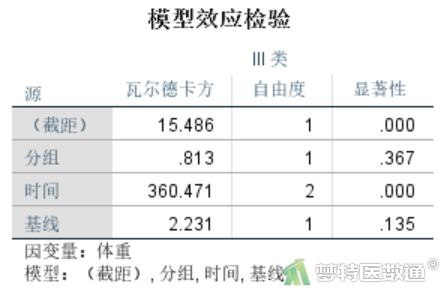
“模型效应检验”结果(图16)提示“时间”的wald χ2=360.471,P<0.001,有统计学意义,表示不同测量时间点的体重增量有差异。“分组”的wald χ2=0.813,P=0.367,无统计学意义,表示不同饲料组的体重增量无差异。
4. 参数估计
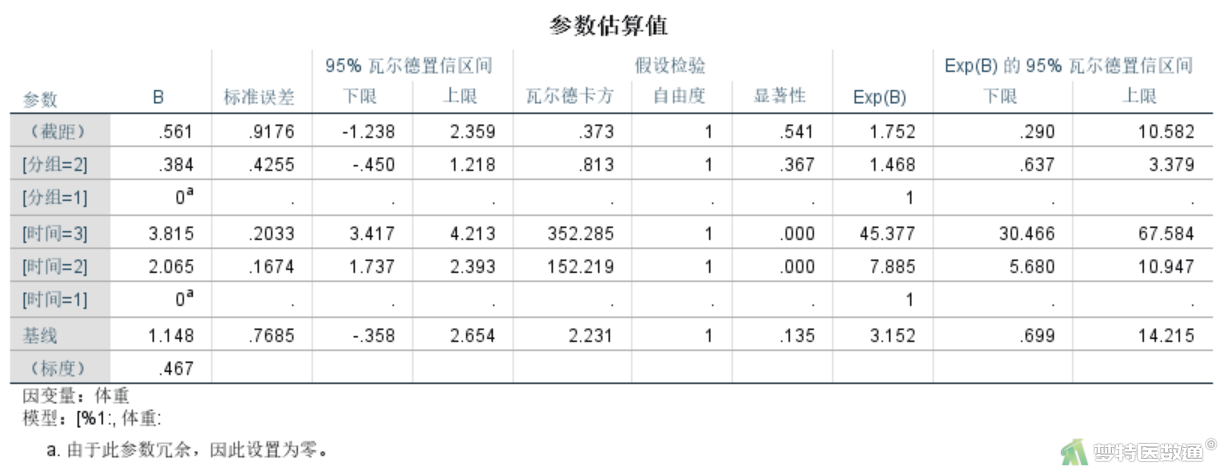
“参数估计”结果(图17)列出了各次测量与第一次测量相比的系数及统计学推断结果,可见各个时间点与第一次测量相比差异均有统计学意义(P<0.001)。如time2体重增量比time1高2.065 kg,time3体重增量比time1高3.815 kg。
B饲料组比A饲料组的体重增量高0.384 kg,差异无统计学意义(P=0.367)。
5. 两两比较
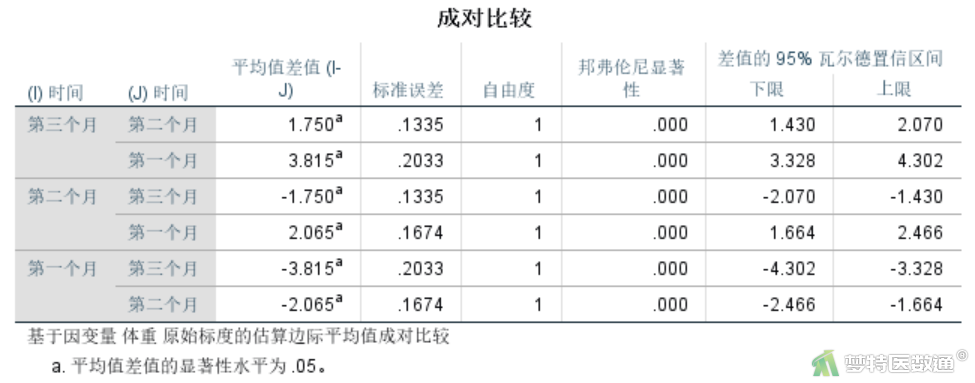
“成对比较”结果(图18)提供了各时间点两两比较的“平均值差值”“标准误差”“显著性(校正P值)”和“差值的95%置信区间”。可知,随着时间的增长,各时刻与time1相比,均数差逐渐增大,且均有统计学意义(P<0.001),结果与“参数估计”结果(图17)一致。
四、结论
本研究采用广义估计方程分析研究A、B两种饲料对家兔的增重效果。组别与时间无交互作用(χ2分组*时间=4.580,P=0.101),故进行主效应分析。
结果显示,校正基线体重后,不同测量时间点的体重增量差异有统计学意义(P<0.001),随着时间的增长,各时刻与time1相比,均数差逐渐增大,且均有统计学意义(P<0.001)。不同饲料组的体重增量差异无统计学意义(P=0.367)。综上可知,两种饲料对家兔的增重效果无差异。
本例分析结果和两因素重复测量协方差分析一(无交互作用)—SPSS软件实现一致。