单因素方差分析(One-Way ANOVA)——Python软件实现

关键词：Python; 单因素方差分析; F检验; Welch检验; 韦尔奇检验; 事后检验; 两两比较

一、案例介绍

某医生用A、B、C3种方案治疗血红蛋白低下的贫血患者，治疗两个月后，记录每名受试者血红蛋白的上升克数。问3种治疗方案对患者贫血的疗效是否有差别？部分数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较3种治疗方案对贫血患者的疗效是否有差别，即判断3种治疗方案患者的血红蛋白上升克数是否存在差异。针对这种情况可以使用单因素方差分析。但需要满足6个条件：

条件1：观察变量为连续变量。本研究中的血红蛋白上升克数为连续变量，该条件满足。

条件2：观测值相互独立。本研究中各研究对象的观测值都是独立的，不存在互相干扰的情况，该条件满足。

条件3：观测值可分为多组(≥3)。本研究中分为A、B、C3组，该条件满足。

条件4：观察变量不存在显著的异常值。该条件需要通过软件分析后判断。

条件5：各组观测值为正态(或近似正态)分布。该条件需要通过软件分析后判断。

条件6：多组观测值的整体方差相等。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

import pandas as pd #导入pandas包
df = pd.read_csv(r'单因素方差分析.csv')
df

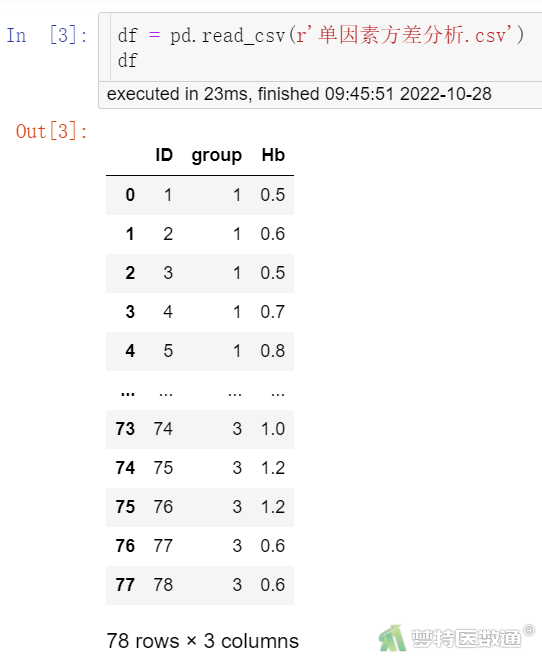
在数据栏目中可以查看全部数据情况(图2)，数据集中共有78例患者的3个变量数据，3个变量分别是被调查者的编号(ID)、治疗分组(group)及血红蛋白的上升克数(Hb)。

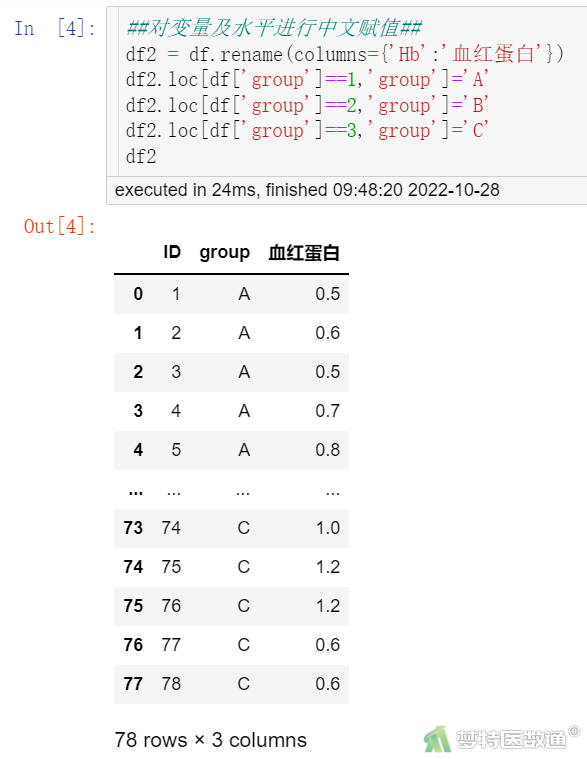
##对变量及水平进行中文赋值##

df2 = df.rename(columns={'Hb':'血红蛋白'})
df2.loc[df['group']==1,'group']='A'
df2.loc[df['group']==2,'group']='B'
df2.loc[df['group']==3,'group']='C'
df2

(二) 适用条件判断

1. 条件4判断(异常值判断)

(1) 软件操作

##分组描述数据子集##

df2.groupby("group").describe()

##分组绘制箱线图##

import matplotlib.pyplot as plt
plt.figure(figsize = (5,3),dpi = 120,facecolor = "white",edgecolor = "red") #建立画布
plt.rcParams['font.family'] = 'SimSun'
plt.boxplot([df2.loc[df2.loc[:,'group']=='A','血红蛋白'],
                     df2.loc[df2.loc[:,'group']=='B','血红蛋白'],
                     df2.loc[df2.loc[:,'group']=='C','血红蛋白']],
                    labels=["A","B","C"])
plt.savefig("boxplot.tif",dpi = 300,bbox_inches = "tight")
plt.show() #展示箱线图

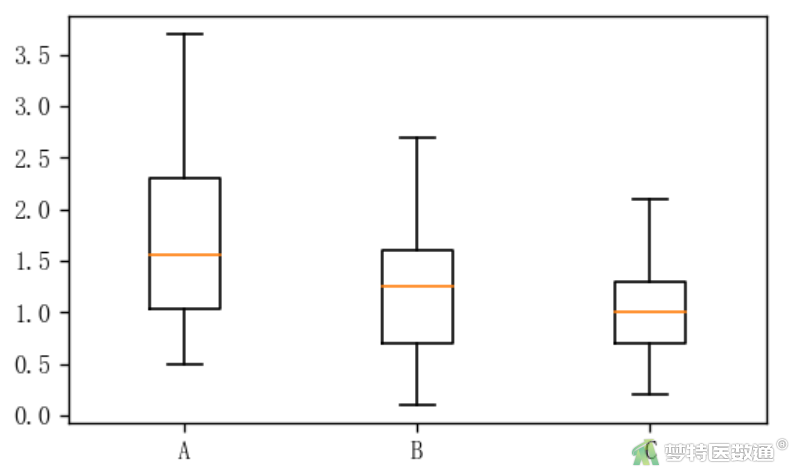
(2) 结果解读

“describe (描述性分析)”命令运行结果(图3)，列出了观察变量的count (总数)、mean(平均数)、std (标准差)、min.(最小值)、25%(第一四分位数)、50% (中位数)、75% (第三四分位数)和max.(最大值)，依据专业可判断血红蛋白的上升克数最大值3.7 g和最小值0.1 g均可能存在；此外，结合箱线图(图4)，可认为无需要删除的异常值，满足条件4。

2. 条件5判断(正态性检验)

(1) 软件操作

##分组绘制Q-Q图##

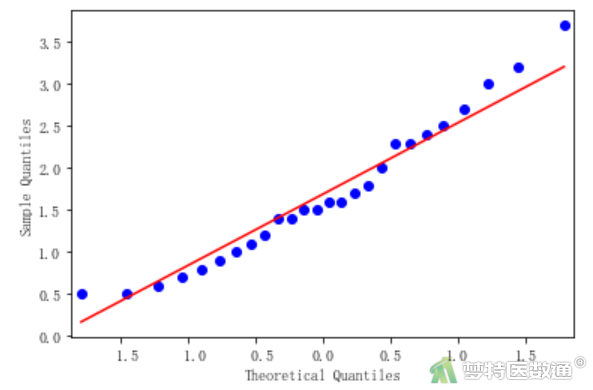
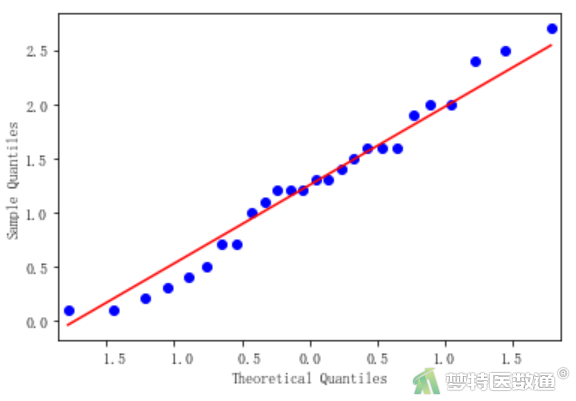
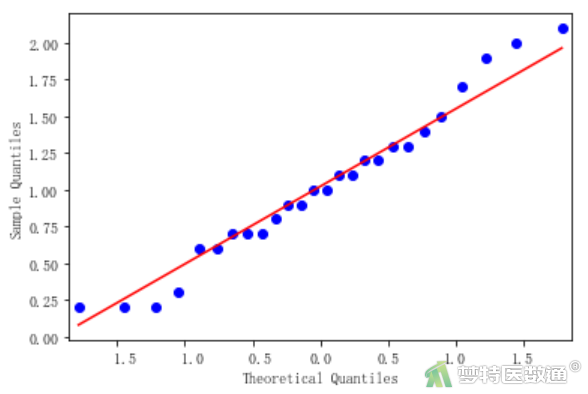
import statsmodels.api as sm #导入statsmodels.api包
import pylab
sm.qqplot(df2.loc[df2.loc[:,'group']=='A','血红蛋白'], line='s') #选取第一组数据
pylab.show() #显示第一组QQ图
sm.qqplot(df2.loc[df2.loc[:,'group']=='B','血红蛋白'], line='s') #选取第二组数据
pylab.show() #显示第二组QQ图
sm.qqplot(df2.loc[df2.loc[:,'group']=='C','血红蛋白'], line='s') #选取第三组数据
pylab.show() #显示第三组QQ图

##正态性检验##

from scipy import stats #导入scipy包
shapiro_test1 = stats.shapiro(df2.loc[df2.loc[:,'group']=='A','血红蛋白']) 
print(shapiro_test1)
shapiro_test2 = stats.shapiro(df2.loc[df2.loc[:,'group']=='B','血红蛋白'])
print(shapiro_test2)
shapiro_test3 = stats.shapiro(df2.loc[df2.loc[:,'group']=='C','血红蛋白'])
print(shapiro_test3)

(2) 结果解读

图5-1、图5-2和图5-3的Q-Q图上3组散点基本围绕对角线分布，提示3组数据呈正态分布；“Shapiro-Wilk normality test (S-W正态性检验)”结果(图6)分别显示3组的P值依次为0.296、0.486、0.435，均＞0.1，也提示3组数据服从正态分布，满足条件5。

3. 条件6判断(方差齐性检验)

(1) 软件操作

##计算标准差##

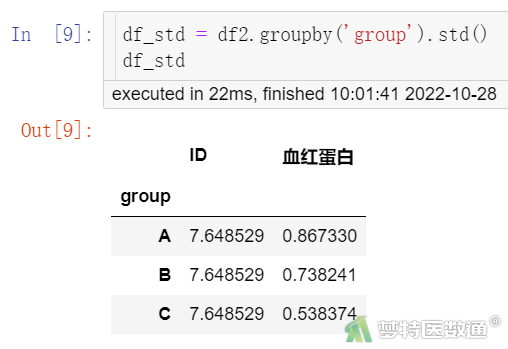
df_std = df2.groupby('group').std()
df_std

##计算均数##

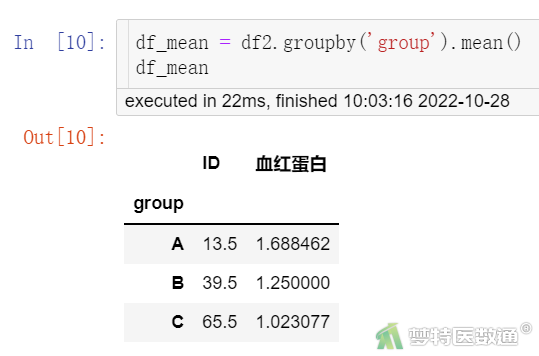
df_mean = df2.groupby('group').mean()
df_mean

##levene法方差齐性检验##

group0 = df2.loc[df2.loc[:,'group']=='A']['血红蛋白'] #选取第一组数据
group1 = df2.loc[df2.loc[:,'group']=='B']['血红蛋白'] #选取第二组数据
group2 = df2.loc[df2.loc[:,'group']=='C']['血红蛋白'] #选取第二组数据
leveneTestRes = stats.levene(group0, group1, group2, center='mean') #levene法齐性检验
print(leveneTestRes) #显示检验结果

(2) 结果解读

描述统计结果(图7、图8）分别显示了各组的标准差和均数。结果显示，A、B、C3组的标准差分别为0.87、0.74、0.54 g，3组的标准差存在差异，但是否有统计学意义还需进一步判断。Levene检验结果(图9)显示，F=2.6102，P=0.08019＜0.1，提示3组数据的方差不齐，不满足条件6。

(三) 统计描述及推断

1. 软件操作

##单因素方差分析##

from scipy import stats
stats.f_oneway(df2.loc[df2.loc[:,'group']=='A']['血红蛋白'],df2.loc[df2.loc[:,'group']=='B']['血红蛋白'],df2.loc[df2.loc[:,'group']=='C']['血红蛋白'])

import pingouin as pg
pg.welch_anova(dv='血红蛋白', between='group', data=df2)

2. 结果解读

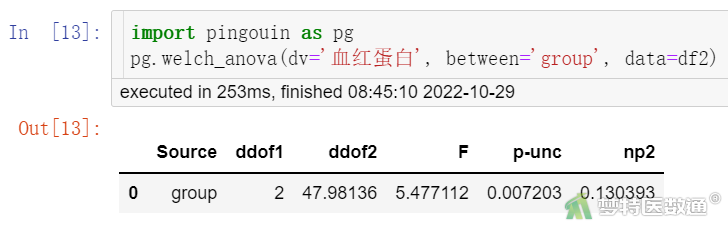
单因素方差分析结果见图10，校正单因素方差分析(Welch’s)结果见图11。本案例满足条件1~5，不满足方差齐性，但方差并非严重不齐，所以采用校正单因素方差分析(Welch’s)法结果，W=5.477，P=0.007；可认为各组均数不全相等(至少有两组均数不相同)。

(四) 事后检验(两两比较)

上面分析得出了“各组均数不全相等”的结论，但是具体是哪些组别之间存在差异尚不清楚，因此需要进行事后检验，开展两两比较。

1. 软件操作

##两两比较##

pg.pairwise_gameshowell(dv='血红蛋白', between='group', data=df2)

#注：当不满足方差齐性时采用“Games-Howell”法进行事后检验

2. 结果解读

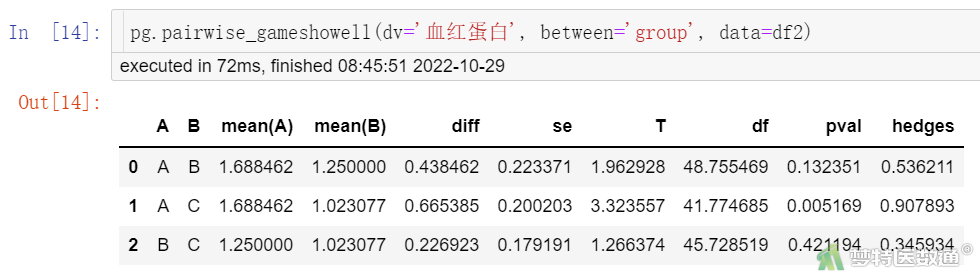
    Games-Howell事后检验结果(图12)显示，A组和B组之间的差异(A-B)为0.438g，差异无统计学意义(P=0.132)；A组和C组之间的差异(A-C)为0.665g，差异有统计学意义(P=0.005)；B组和C组之间的差异(B-C)为0.227g，差异无统计学意义(P=0.421)。因此，可知A组血红蛋白的上升克数比C组高0.665 g，差异有统计学意义(P=0.005)。

四、结论

本研究采用单因素方差分析判断3种方案治疗后，贫血患者的血红蛋白上升克数是否存在差异。通过专业知识判断，3组数据不存在需要删除的异常值；通过绘制Q-Q图和Shapiro-Wilk检验，提示3组数据满足正态分布；通过Levene’s检验，提示3组数据间方差不齐，采用校正单因素方差分析(Welch’s)法分析数据。

分析结果显示，A、B、C3组血红蛋白的上升克数分别为1.69±0.87、1.25±0.74、1.02±0.54 g，3组均数不全相等(F=5.48，P=0.007)。进一步采用Games-Howell法进行两两比较，显示A组血红蛋白的上升克数比C组高0.665 g，差异有统计学意义(P=0.005)；A组血红蛋白的上升克数比B组高0.438 g，差异无统计学意义(P=0.132)；B组血红蛋白的上升克数比C组高0.227 g，差异无统计学意义(P=0.421)。因此，A方案治疗贫血患者后血红蛋白上升克数增长最快，可认为A方案疗效最好。

五、分析小技巧

(一) 正态性检验

严格来讲，单因素方差分析时，需要分别对每一组数据的正态性进行检验。但方差分析对数据的分布具有一定的耐受力，如果数据不是严重偏态或者只有部分组别数据不满足正态性要求，鉴于参数检验的统计学效能优于非参数检验的角度，还是可以使用单因素方差分析方法，而不使用非参数检验。

单因素方差分析时，也可考察整体数据的正态性情况。如上所述，单因素方差分析对数据分布具有一定的耐受力，如果数据满足整体正态分布，也是可以使用该种分析方法。但我们建议尽可能分组别检验数据的正态性。关于正态性检验的注意事项详见文章医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现。

(二) 方差齐性检验

对于不是特别严重的方差不齐，单因素方差分析提供了校正检验方法(Welch’s)，是考虑了方差差异之后的更为稳健的分析结果。但当组间方差差异较大时，校正结果也不一定可信，建议使用非参数检验(Kruskal-Wallis H检验)。如果数据正态性和方差齐性都不满足，最好使用非参数检验(Kruskal-Wallis H检验)。关于方差齐性检验的更多内容请阅读医学统计学核心概念及重要假设检验的软件实现(4/4)——方差齐性检验及SPSS实现。

(三) 事后检验(两两比较)

多重比较一般分为事前检验(Prior tests)和事后检验(Post hoc tests)。事前检验是指在数据收集之前便决定了要通过多重比较来考察多个组与某个特定组之间的差别，多根据专业意义设定比较的策略。如果是事前检验，不论整体分析的结果如何，均可进行比较，并且一般不需要对检验水准进行太多修正。事后检验只有在方差分析得到有统计学意义的结果后才进行，是一种探索性分析。对于事先未计划的多重比较(即事后检验)，各组间的差异只是一种提示，要确认这种差异最好重新设计实验。

事前检验(Prior tests)最常用的两两比较方法有LSD法和Dunnett-t检验。事后检验(Post hoc tests)最常用的方法有SNK法、Duncan法、Turkey’b和Scheffe法。

LSD法是最灵敏的方法，因此也容易犯假阳性错误。Dunnett-t法多用于多个实验组与一个对照组比较，此时应指定对照组，多用于确证性研究，少用于探索性研究。Bonferroni法是对LSD法的严格校正，结果更加保守，但当组数较多时，较难发现组间差异，因此如果各组例数相差不大且组数不多时可采用。当不满足方差齐性时常采用“Games-Howell”法进行事后检验。