两因素方差分析(Two-Way ANOVA)一(无交互作用)——Python软件实现

关键词：Python; 两因素方差分析; 交互作用; 主效应; 单独效应; 简单效应

一、案例介绍

研究A、B两种镇痛药物联合运用对癌症患者的镇痛效果。药物A取3个剂量：1.0、2.5、5.0 mg；药物B也取3个剂量：5、15、30 μg，共9个处理组。将27例研究对象随机分成9组，每组3例，记录每名对象的镇痛时间Time (min)。试分析A、B两药联合运用的镇痛效果。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是分析A、B两药联合运用的镇痛效果。临床上，药物之间联合运用往往会相互影响，这种影响可能为正向的增强效应，也可能为反向的拮抗作用。针对这种情况，可以使用多因素方差分析。由于本案例为药物A和药物B两个因素，因此可以使用两因素方差分析。但需要满足6个条件：

条件1：观察变量唯一，且为连续变量。本研究中观察变量只有镇痛时间，且为连续变量，该条件满足。

条件2：有两个因素，且都为分类变量。本研究中有药物A、药物B两个因素，都为分类变量，该条件满足。

条件3：观测值相互独立。本研究中各研究对象的观测值都是独立的，不存在互相干扰的情况，该条件满足。

条件4：观察变量不存在显著的异常值。该条件需要通过软件分析后判断。

条件5：各组、各水平观测值为正态(或近似正态)分布。该条件需要通过软件分析后判断。

条件6：相互比较的各处理水平(组别)的总体方差相等，即方差齐同，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

import pandas as pd #导入pandas包
df = pd.read_csv(r'两因素方差分析一.csv')  #导入CSV数据
pd.set_option('display.max_rows', 10)
df  #查看数据

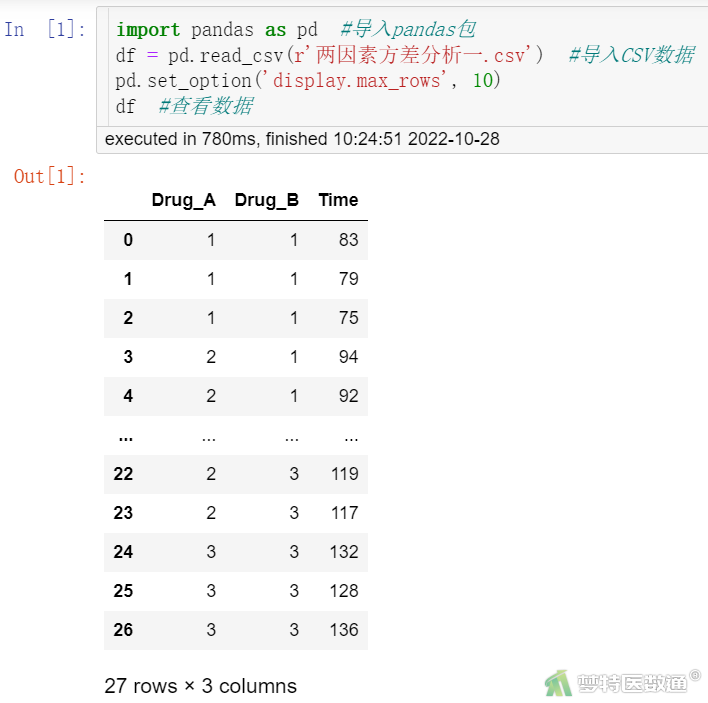
数据栏目(图1)可以查看全部数据情况，数据集中共有3个变量和27例观察数据，3个变量分别代表A种药物(Drug_A)、B种药物(Drug_B)和镇痛时间(Time)。

(二) 适用条件判断

条件4~条件6需要通过模型残差进行判断，因此先生成模型残差。

1. 生成模型残差

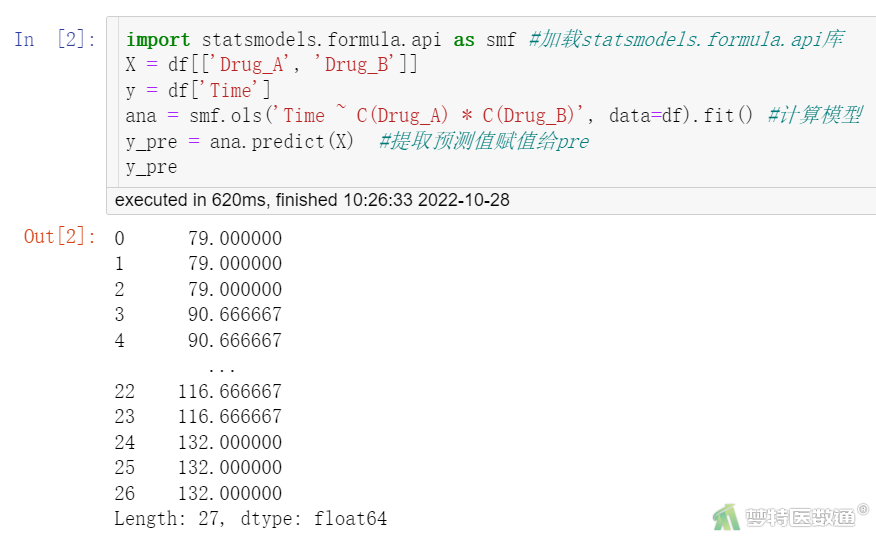
##计算模型，得预测值(图2)##

import statsmodels.formula.api as smf #加载statsmodels.formula.api库
X = df[['Drug_A', 'Drug_B']]
y = df['Time']
ana = smf.ols('Time ~ C(Drug_A) * C(Drug_B)', data=df).fit() #计算模型
y_pre = ana.predict(X)  #提取预测值赋值给pre
y_pre 

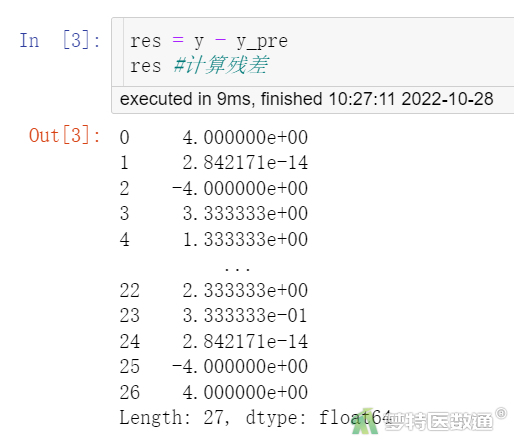
## 数据整理及残差值提取(图3)##

res = y - y_pre
res #计算残差

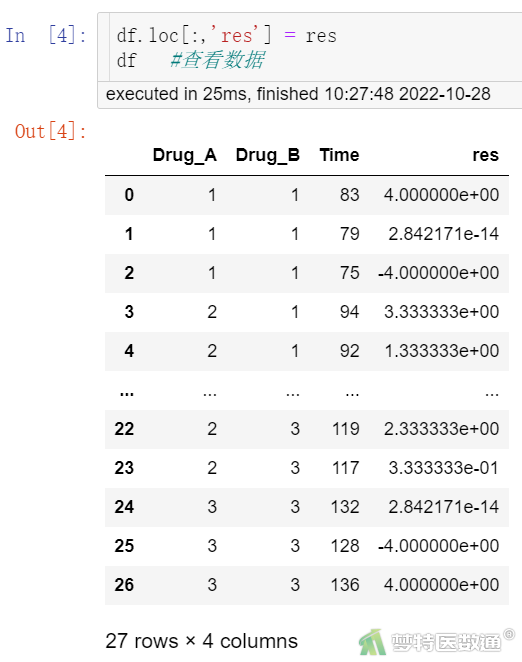
## 合并数据(图4)##

df.loc[:,'res'] = res
df   #查看数据

2. 条件4判断(异常值判断)

(1) 软件操作

## 绘制箱线图 ##

import matplotlib.pyplot as plt
import seaborn as sns
sns.boxplot(x = 'Drug_A', y = 'res', data = df,hue='Drug_B')  #绘制箱线图
plt.legend(loc = (1.02,0.35),title='Drug_B')
plt.show()

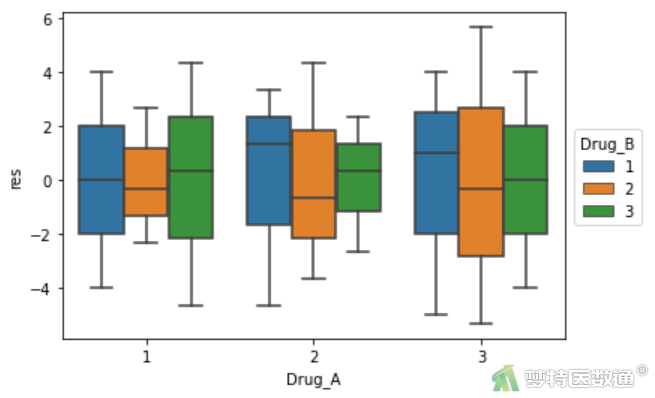
(2) 结果解读

残差的箱线图(图5)未提示任何异常值和极端值，满足条件4。

3. 条件5判断(正态性检验)

(1) 软件操作

## 正态性检验 ##

from scipy.stats import shapiro
shapiro(df.res)

(2) 结果解读

正态性检验结果(图6)显示P=0.0896>0.05且较为接近0.1，提示因变量残差近似服从正态分布，满足条件5。

4. 条件6判断(方差齐性检验)

(1) 软件操作

## 方差齐性检验 ##

import pingouin as pg
df.loc[:,'group'] = df.apply(lambda x: "%d_%d"%(x["Drug_A"],x["Drug_B"]),axis = 1)
print(pg.homoscedasticity(df, dv='res', group='group',method='levene',center = 'mean'))

(2) 结果解读

       Levene’s方差齐性检验结果(图7)显示，F=0.3043、P=0.9546；提示数据总体方差相等，满足条件6。

(三) 统计描述

1. 软件操作

##数据分组描述##

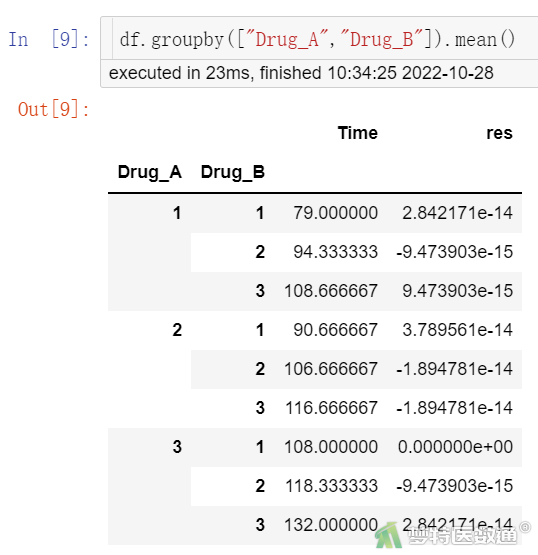
df.groupby(["Drug_A","Drug_B"]).mean()

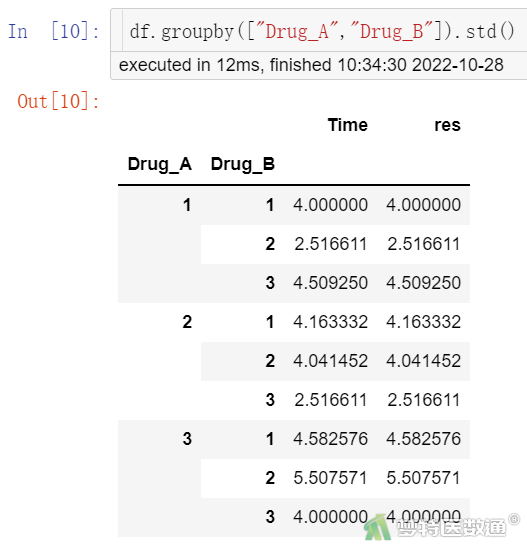
df.groupby(["Drug_A","Drug_B"]).std()

2. 结果解读

       各组的均数和标准差见图8~9，可知A药在1.0 mg水平，B药为5.0、15.0、30.0 μg水平时，镇痛时间分别为79.00±4.00、94.33±2.52、108.67±4.51min；A药在2.5 mg水平，B药为5、15、30 μg水平时，镇痛时间分别为：90.67±4.16、106.67±4.04、116.67±2.52 min；A药在5.0 mg水平，B药为5、15、30 μg水平时，镇痛时间分别为：108.00±4.58、118.33±5.51、132.00±4.00 min。

(四) 两因素方差分析

1. 软件操作

## 绘制边际均数图 ##

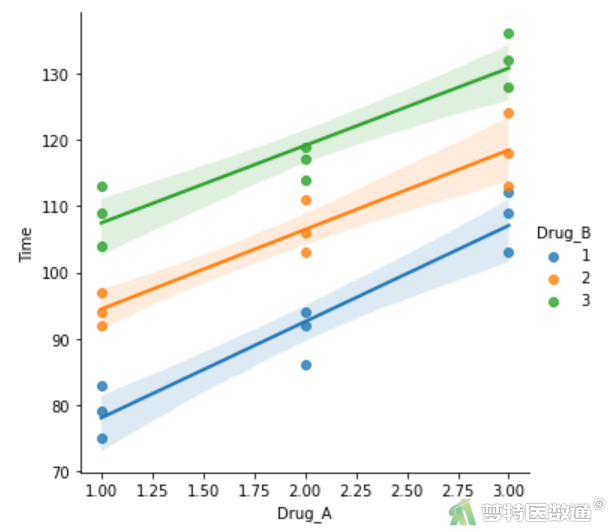
import seaborn
seaborn.lmplot(y='Time', x = 'Drug_A', hue = 'Drug_B',data=df)
plt.show()

2. 结果解读

边际均数图(图10)显示了各组镇痛时间的变化情况，可见两药物的变化曲线基本平行，不存在明显的交互作用。

(五) 交互作用判断

本案例有两个因素(一个为A药，另一个为B药)，因此需要首先判断两个因素(药物)之间是否存在交互作用。如果交互作用有统计学意义，则需要分析单独效应。此时，单纯研究某个因素的作用并无意义，应分别探讨另一个因素不同水平时对该因素的作用。

1. 软件操作

from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
formula = 'Time~ C(Drug_A)+C(Drug_B)+C(Drug_A) * C(Drug_B) '
anova_results = anova_lm(ols(formula,df).fit())
print(anova_results) #查看方差检验结果

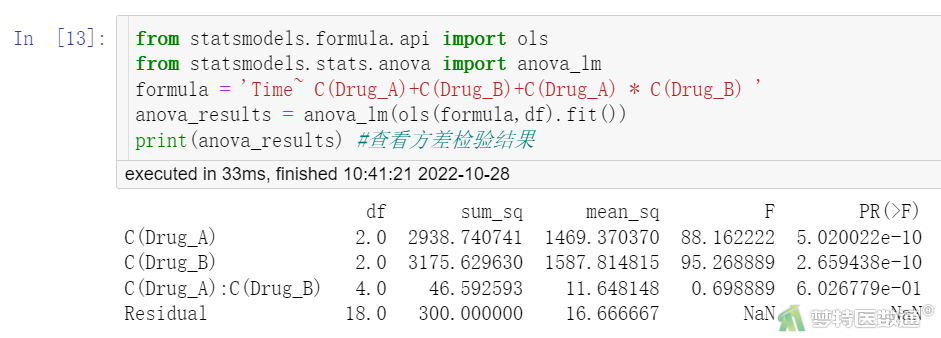
2. 结果解读

       方差分析结果(anova_results)见图11，Drug_A与Drug_B之间的交互作用结果为F_{Drug_A*Drug_B}=0.699，P=0.603，提示Drug_A与Drug_B之间的交互作用无统计学意义。因此，本案例可直接以主效应分析结果进行判断，如果交互作用有统计学意义，则需要分析单独效应。

(六) A药主效应分析

A药的主效应检验结果(图11)显示，F_{Drug_A}=88.162，P<0.001，认为不同药物浓度时，镇痛时间差异有统计学意义。

(七) B药主效应分析

       B药的主效应检验结果(图11)显示，F_{Drug_B}=95.269，P<0.001，认为不同药物浓度时，镇痛时间差异有统计学意义。

(八) 事后检验(两两比较)

       A、B药物在不同药物浓度时，镇痛时间差异均有统计学意义的结论，因此需要进行事后检验，开展两两比较。

1. 软件操作

## 事后检验 ##

from statsmodels.stats.multicomp import pairwise_tukeyhsd
print(pairwise_tukeyhsd(df ['Time'], df ['Drug_A']))
print(pairwise_tukeyhsd(df ['Time'], df ['Drug_B']))

2. 结果解读

事后检验比较-Drug A(TukeyHSD)结果(图12)提供了A药不同浓度间两两比较的meandiff (均数差)、p-adj (调整过后的P值)、lower (95%置信区间下限)、upper (95%置信区间上限)和reject (是否拒绝此假设)。可知，2.5 mg和1.0 mg与5.0 mg相比，均数差逐渐增大。5 mg比2.5 mg时均数增加了14.778 min，比1.0 mg时均数增加了25.444 min，差异有统计学意义(P<0.05)。表明随着A药药物浓度增加，镇痛时间呈上升趋势。

事后检验比较-Drug B(TukeyHSD)结果(图12)提供了B药不同浓度间两两比较的meandiff (均数差)、p-adj (调整过后的P值)、lower (95%置信区间下限)、upper (95%置信区间上限)和reject (是否拒绝此假设)。可知，15.0 μg和30.0 μg与5.0 μg相比，均数差逐渐增大。15.0 μg比5.0 μg时均数增加了13.889 min，至30.0 μg时增加了26.556 min，差异均有统计学意义(P<0.05)。表明随着B药药物浓度增加，镇痛时间呈上升趋势。

四、结论

本研究采用两因素方差分析探讨A、B两种镇痛药物联合运用在癌症患者的镇痛效果。通过专业知识判断，数据不存在异常值；通过Shapiro-Wilk检验，提示各组数据服从正态分布；通过Levene’s检验，提示数据总体方差相等；两药物之间无交互作用(F_{Drug_A*Drug_B}=0.699，P=0.603)，故进行主效应分析。

A药在1.0 mg水平，B药为5.0、15.0、30.0 μg水平时，镇痛时间分别为：79.00±4.00、94.33±2.52、108.67±4.51min；A药在2.5 mg水平，B药为5、15、30 μg水平时，镇痛时间分别为90.67±4.16、106.67±4.04、116.67±2.52 min；A药在5.0 mg水平，B药为5、15、30 μg水平时，镇痛时间分别为108.00±4.58、118.33±5.51、132.00±4.00 min。A药的主效应检验结果为F_{Drug_A}=88.162，P<0.001，认为不同药物浓度时，镇痛时间差异有统计学意义。B药的主效应检验结果为F_{Drug_B}=95.269，P<0.001，认为不同药物浓度时，镇痛时间差异有统计学意义。进一步采用“Tukey's HSD”校正法进行两两比较可知，A药2.5 mg和1.0 mg与5.0 mg相比，均数差逐渐增大，差异均有统计学意义(P<0.05)；表明随着A药药物浓度增加，镇痛时间呈上升趋势。B药15.0 μg和30.0 μg与5.0 μg相比，均数差逐渐增大，差异均有统计学意义(P<0.05)。表明随着B药药物浓度增加，镇痛时间呈上升趋势。综上可知，不同剂量药物A的镇痛效果不同，不同剂量药物B的镇痛效果不同，A、B两种药物不存在交互作用。