在前面文章中介绍了随机区组设计方差分析(Randomized Block Design ANOVA)——R软件实现和两阶段交叉设计方差分析(Two-stage Cross-over Design ANOVA)——R软件实现,本文进一步介绍仅研究主效应的实验设计中的拉丁方设计方差分析(Latin Square Design ANOVA)在R软件中的实现步骤。
关键词:R; 拉丁方设计; 方差分析; 仅研究主效应的实验设计
在医学研究中,随机区组设计涉及一个处理因素、一个区组因素;若实验研究涉及一个处理因素和两个区组因素,且每个因素的水平数相等,此时可采用拉丁方设计来安排实验,将两个区组因素分别安排在拉丁方设计的行和列上。需要注意的是,由于处理因素只有一个,因此此种设计仍为单因素设计实验。拉丁方设计是在随机区组设计的基础之上发展而来,可以多安排一个对实验结果有影响的非处理因素,增加了均衡性,减少了误差,提高了效率。
一、案例介绍
假设某研究者欲比较A、B、C、D、E、F6种饲料(feed,A~F依次对应1~6)对大鼠的增重效果(weight, g)。采用拉丁方设计,选用6只体重相近的出窝雄性大鼠(row_block)并在每天固定的6个时间点(col_block)给大鼠喂养相同重量的饲料。试对该拉丁方设计的实验结果进行方差分析。部分数据见图1。本案例数据可从“附件下载”处下载。
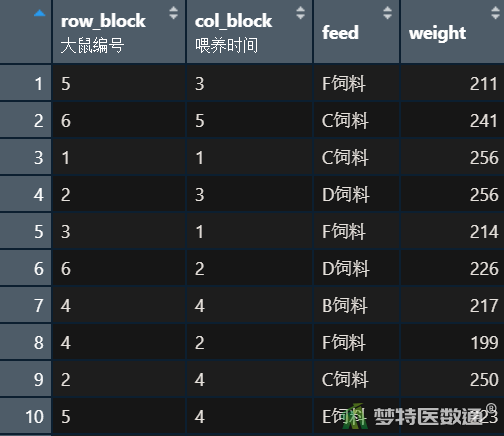
二、问题分析
在拉丁方设计资料分析时采用三向分类的方差分析(three-way classification ANOVA)。总变异可分解为处理组变异、行区组变异、列区组变异和误差4部分,需要满足6个条件:
条件1:观察变量唯一,且为连续变量。本研究中观察变量为体重增量,为连续变量,该条件满足。
条件2:有3个因素,且都为分类变量。本研究中有处理效应(A~F六种饲料)及两个区组因素(大鼠编号、喂养时间),都为分类变量,该条件满足。
条件3:观测值相互独立。本研究中各研究对象的观测值都是独立的,不存在互相干扰的情况,该条件满足。
条件4:相互比较的各处理水平(组别)的总体方差相等,即方差齐同,可采用方差齐性检验。实际上,当各组样本含量相等或接近时,即使方差不齐,方差分析结果仍然稳健。该条件需要通过软件分析后判断。
条件5:各组、各水平观测值为正态(或近似正态)分布。该条件需要通过软件分析后判断。
条件6:观察变量不存在显著的异常值。该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 导入数据(图2)
mydata = read.csv("拉丁方设计.csv", header = T)
str(mydata)

##转换变量类型,添加标签##
mydata$feed <- factor(mydata$feed, levels = c(1, 2, 3, 4, 5, 6), labels = c("A饲料", "B饲料", "C饲料", "D饲料", "E饲料", "F饲料"))
mydata$row_block <- factor(mydata$row_block)
mydata$col_block <- factor(mydata$col_block)
attr(mydata$row_block, "label") = "大鼠编号"
attr(mydata$col_block, "label") = "喂养时间"
(二) 适用条件判断
条件4~6需要通过模型残差进行判断,因此先生成模型残差。
1. 生成模型残差
##数据整理及残差值提取## AOV <- aov(weight ~ feed + row_block + col_block, mydata) #计算方差分析模型 res <- rstandard(AOV) #提取标准化残差赋值给res pre <- predict(AOV) #提取预测值赋值给pre mydata <- data.frame(mydata, res, pre) #重新形成数据集 View(mydata) #查看数据
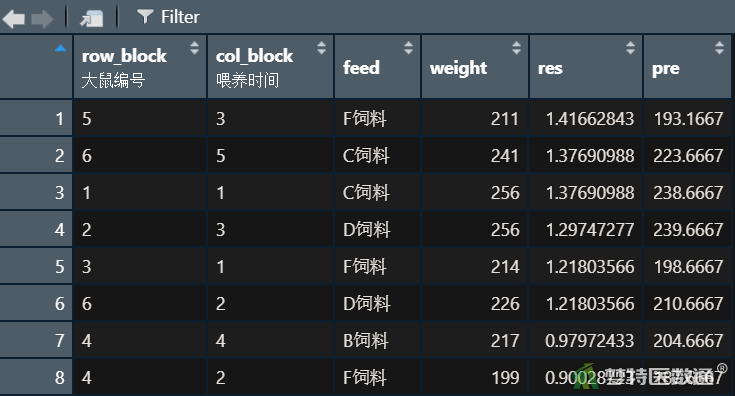
2. 条件4判断(方差齐性检验)
(1) 软件操作
##方差齐性检验##
此处通过对残差进行单因素方差分析判断数据的方差齐性。
fit <- aov (res ~ feed, mydata)

(2) 结果解读
图4方差齐性检验结果显示P=1.0,提示相互比较的各处理水平的总体方差相等。本案例满足条件4。
3. 条件5判断(正态性检验)
(1) 软件操作
##正态性检验##
shapiro.test(mydata$res)
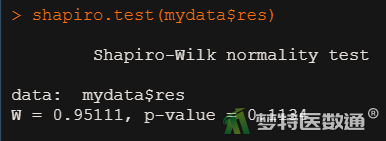
(2) 结果解读
图5正态性检验结果显示P=0.1134>0.1,提示因变量残差近似服从正态分布。本案例满足条件5。
4. 条件6判断(异常值)
(1) 软件操作
##绘制箱线图##
library(ggplot2) #调用包“ggplot2”
boxp <- ggplot(mydata, aes(res))+
stat_boxplot(geom = 'errorbar')+ #添加误差线
geom_boxplot() #绘制箱线图
boxp
ggsave("boxp.png", width=8, height=5, dpi=300) #保存图片
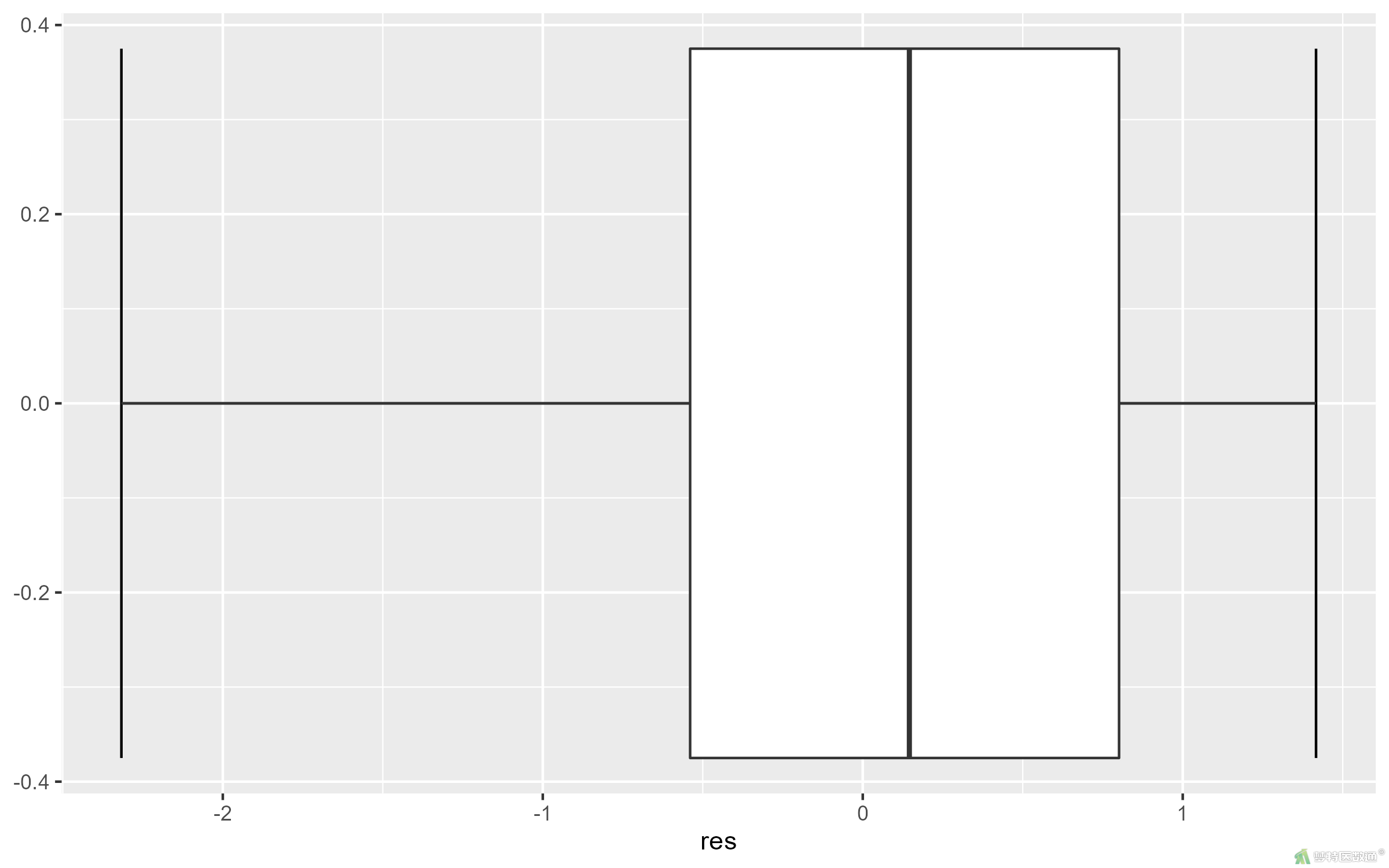
(2) 结果解读
残差的箱线图将被保存在R数据分析路径下,图6残差的箱线图未提示任何异常值和极端值,满足条件6。
(三) 统计描述
1. 软件操作
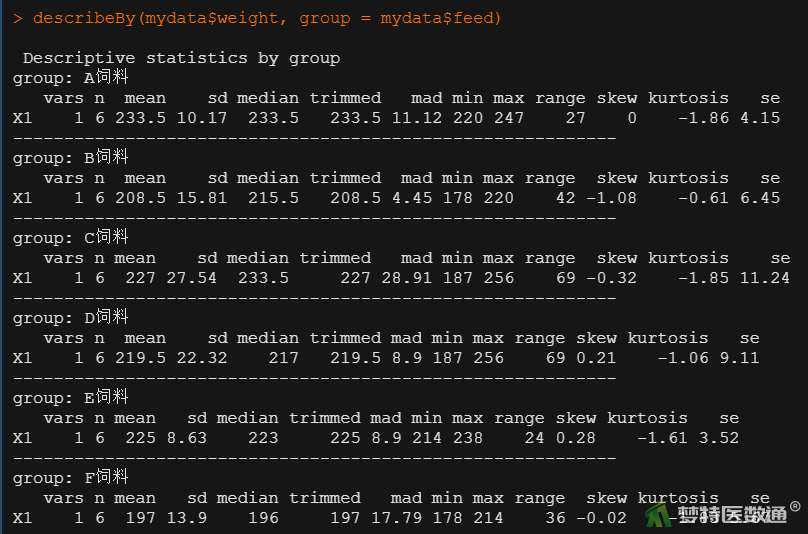
##数据分组描述## library(psych) #调用包“psych” describeBy(mydata$weight, group = mydata$feed)
2. 结果解读
图7列出了处理组各组的均值和标准差,可知A、B、C、D、E、F 6种饲料的大鼠体重增量分别为233.50±10.17、208.50±15.81、227.00±27.54、219.50±22.32、225.00±8.63、197.00±13.90 g。
(四) 三因素方差分析
1. 软件操作
##查看方差分析结果## summary(AOV) ##采用SNK法进行两两比较## library(agricolae) AOV_snk <- SNK.test(AOV, "feed", group = FALSE) AOV_snk$comparison
2. 结果解读
图8为拉丁方设计的方差分析结果。可知处理效应(不同饲料)之间的差异有统计学意义(P=0.014),两区组效应间差异均无统计学意义(P>0.1)。
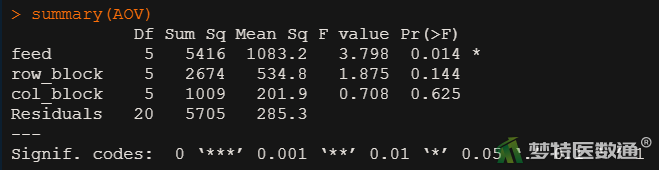
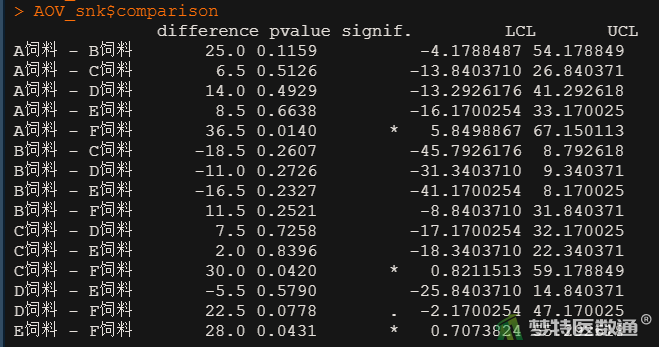
图9为进一步的两两比较分析结果。可见,饲料A (233.50±10.17)与饲料F (197.00±13.90)相比,效应差异有统计学意义(P=0.0140)。饲料C (227.00±27.54)与饲料F (197.00±13.90)相比,效应差异有统计学意义(P=0.0420)。饲料E (225.00±8.63)与饲料F (197.00±13.90)相比,效应差异有统计学意义(P=0.0431)。其余饲料之间的差异尚无统计学意义(P>0.05)。
四、结论
本研究采用拉丁方设计分析六种饲料对大鼠的增重效果。通过库克距离判断,数据不存在需要特殊处理的异常值;通过对残差进行正态性检验,提示数据服从正态分布;通过对残差进行统计学推断,提示6组饲料组数据间方差齐。
分析结果显示,A、B、C、D、E、F 6种饲料的大鼠体重增量分别为233.50±10.17、208.50±15.81、227.00±27.54、219.50±22.32、225.00±8.63、197.00±13.90 g。不同饲料喂养的大鼠体重增量差异有统计学意义(F=3.798,P=0.014)。通过SNK法进行事后检验两两比较发现,饲料A与饲料F相比,效应差异有统计学意义(P=0.0140),饲料C与饲料F相比,效应差异有统计学意义(P=0.0420),饲料E与饲料F相比,效应差异有统计学意义(P=0.0431),其余饲料之间的差异尚无统计学意