前面文章介绍了独立样本t检验的相关理论(独立样本t检验(two-sample/group t-test)——理论介绍)和汇总资料的独立样本t检验(汇总资料的独立样本t检验(two-sample/group t-test) ——MedCalc软件实现),本文介绍几何均数的独立样本t检验在MedCalc软件中的操作过程。
关键词:MedCalc; t检验; 独立样本t检验; 几何均数
在生物医学中,有些资料并不适合使用算数平均数描述其集中趋势,如抗体滴度、疾病潜伏期、水果农药残留等,这类资料一般服从对数正态或近似对数正态分布,适宜使用几何平均值表示其平均水平。当对该类数值进行几何平均值的假设检验时,应先进行变量的对数变换,以改善其正态性和方差齐性,以满足t检验、方差分析等参数检验的适用条件。
一、案例介绍
现检测了115例老年人和116例青年人的某抗体效价,试比较两组的平均效价有无差异?部分数据见图1。案例可从“附件下载”处下载。

本案例的分析目的是比较两组抗体滴度的平均效价有无差异。针对这种情况可以使用几何均数的独立样本t检验进行分析,数据需要满足6个条件:
条件1:观察变量为连续变量。本研究中的抗体滴度经对数转换后,含量为连续变量,该条件满足。
条件2:观察变量相互独立。本研究中各研究对象的观测值都是独立的,不存在互相干扰的情况,该条件满足。
条件3:观察变量分为2组。本研究中分为老年人和青年人组,该条件满足。
条件4:观察变量不存在显著的异常值,该条件需要通过软件分析后判断。
条件5:各组观察变量为正态(或近似正态)分布,对于抗体滴度一般考察经lg转换后的正态性,该条件需要通过软件分析后判断。
条件6:两组观察变量的方差相等,对于抗体滴度一般考察经lg转换后的方差齐性,该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 适用条件判断
对于本案例数据,条件1、2、3均满足。下面判断条件4、5、6。
1. 条件4判断(异常值检测)
以检测老年组的异常值为例进行介绍。
(1) 软件操作
选择“统计”—“异常值检测”,打开“异常值检测”对话框,见图2。

在“异常值检测”对话框(图3),“变量”下选择变量“Antibody”,“筛选条件”下输入“group=1”;“异常值检测方法”下勾选“Grubbs-两侧”、“生成的ESD检验”(“检验最大量的异常值”中输入10)、“Tukey”;“选项”下勾选“对数变换”。

(2) 结果解读
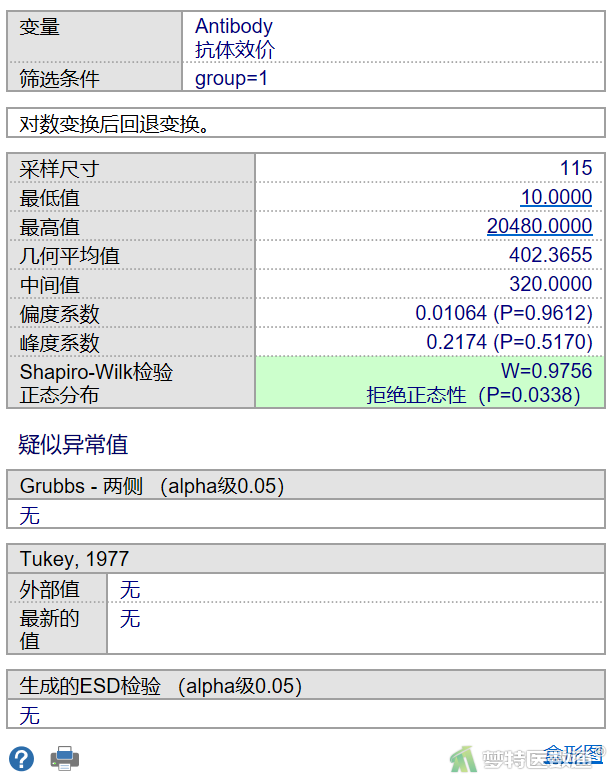
图4为老年人组的异常值检测结果,提示无异常值。
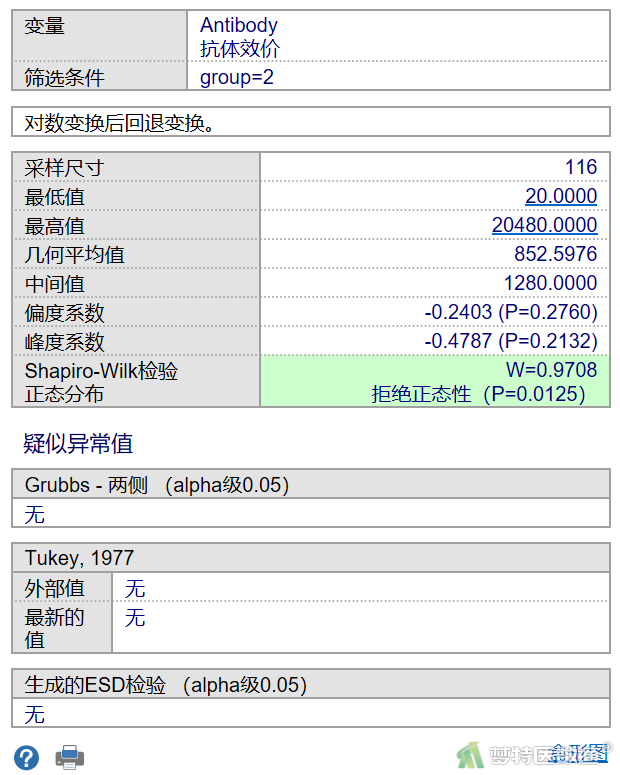
同样操作可得到青年人组的异常值检测结果(图5),也提示无异常值。
2. 条件5判断(正态性检验)
在异常值检测过程中同时输出了正态性检验的结果。从图4可知老年人组正态性检验结果为W=0.9756,P=0.0338;青年人组正态性检验结果为W=0.9708,P=0.0125。尽管两组的P值均<0.1或0.05,但相比原始数据其正态性均得到了极大的改善。由于独立样本t检验对正态性具有一定的容忍度,以及两组数据满足方差齐性,综合考虑,此处对正态性不做硬性要求。
3. 条件6判断(方差齐性检验)
详见下文。
(二) 统计描述及推断
1. 软件操作
选择“统计”—“T检验”—“独立样本t检验” (图6),打开“独立样本t检验”对话框。

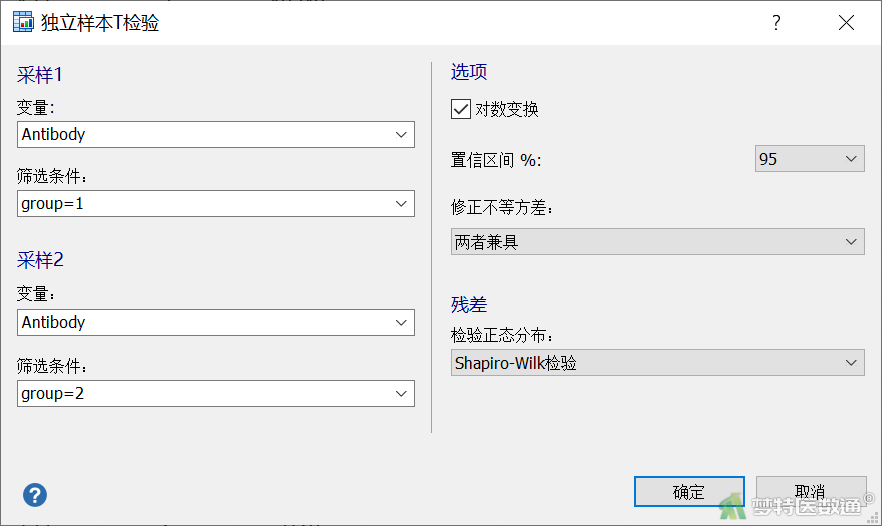
在“独立样本t检验”界面,”采样1”的“变量”下选择“Antibody”,筛选条件中输入“group=1”,”采样2”的“变量”下选择“Antibody”,筛选条件中输入“group=2”,勾选”对数变换”,“置信区间%”下选“95”,“修正不等方差”下选择“两者兼具”,“检验正态分布”下选择“Shapiro-Wilk检验 (夏皮罗-威尔克正态性检验,S-W检验)。”见图7。
2. 结果解读
(1) 条件6判断(方差齐性检验)
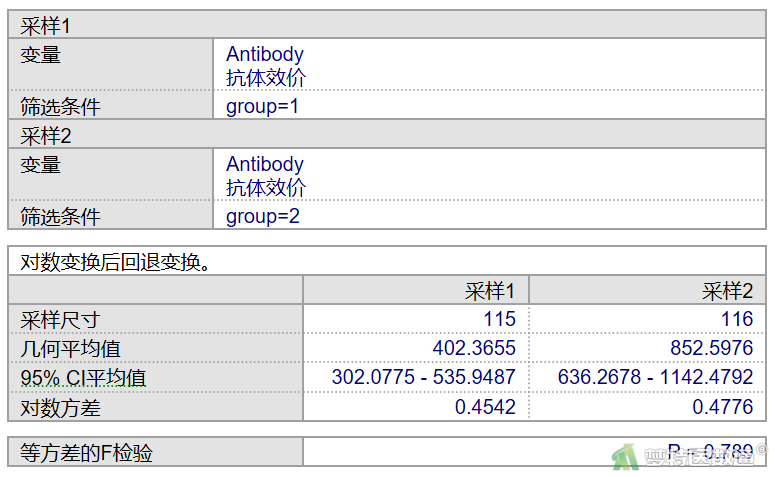
由图8 的“等方差的F检验”结果可知,P=0.789,提示方差齐。
(2) 统计描述
图8为统计学描述结果,可知老年人组 (group=1)的平均效价为1:402.3655,其效价倒数的几何平均值的95%CI为 302.0775~535.9487;青年人组 (group=2)的平均效价为1:852.5976,其效价倒数的几何平均值的95%CI为636.2678~ 1142.4792。从均值看两组的效价存在差异,由于两个95%CI不重叠,按检验水准0.05,可认为两组平均抗体效价不同,青年组的抗体效价更高。
(3) 统计推断
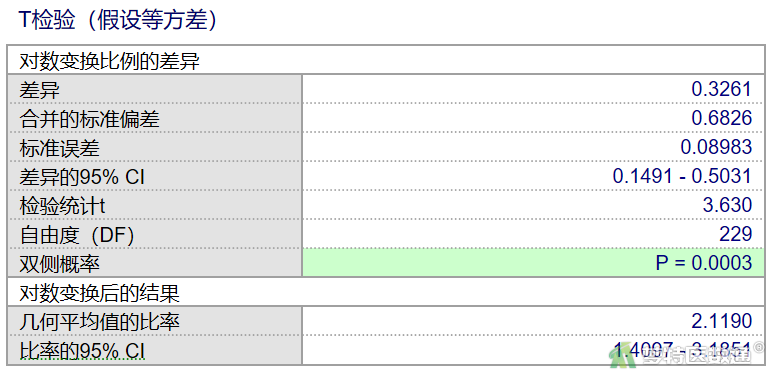
由于本研究方差齐,所以查看“T检验(假设等方差)”的分析结果(图9)。两组效价倒数对数变换后平均值差为0.3261,平均值差的95%CI为0.1491~0.5031,按检验水准0.05,可认为两组平均值的差值与0的差异有统计学意义。两独立样本t检验统计学推断的t= 3.630,P= 0.0003,与上述推断结果一致。
此外,MedCalc还计算了两组几何平均值之比为852.5976/402.3655= 2.1190,95%CI为1.4097~3.1851,按检验水准α=0.05,可认为两组两组几何平均值之比与1的差异有统计学意义,表明两组抗体效价的平均值不同。
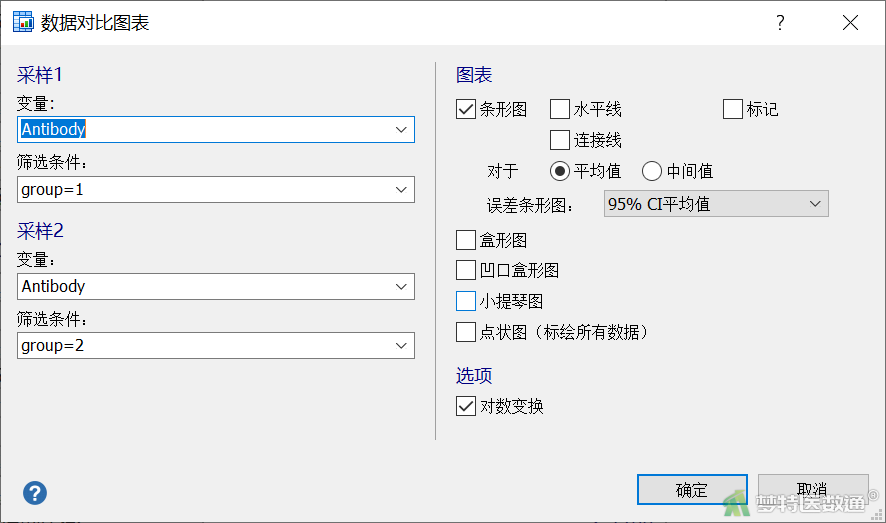
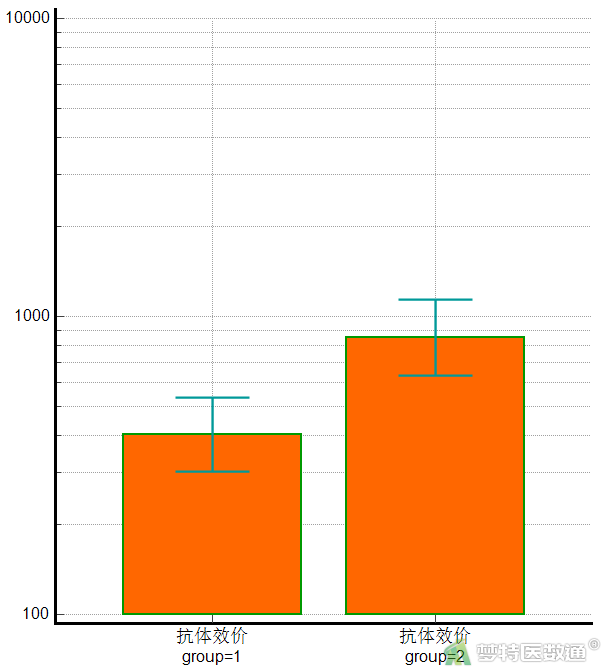
点击分析结果最右下角的“数据对比图表”,按照图10设置相应参数,可得到两组抗体效价的误差条形图(图11)。
四、结论
本研究采用独立样本t检验判断两年人组和青年人组的抗体平均效价有无差异。通过对数转换后,数据不存在需要处理的异常值,两组数据正态性得到了改善,满足方差齐性,符合使用几何均数的独立样本t检验的条件。
结果显示,老年人组的平均效价为1:402.3655,其效价倒数的几何平均值的95%CI为 302.0775~535.9487;青年人组的平均效价为1:852.5976,其效价倒数的几何平均值的95%CI为636.2678~1142.4792;差异有统计学意义(t= 3.630,P= 0.0003)。研究结果表明,老年人组的抗体效价低于青年人组。