生存曲线比较的Log-rank检验——MedCalc软件实现

关键词：MedCalc;生存分析; Kaplan-Meier; log-rank检验

一、案例介绍

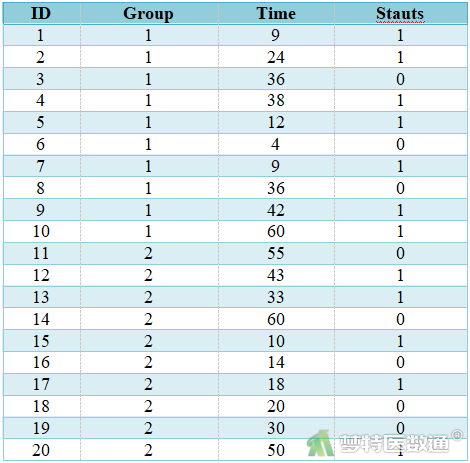
研究人员对20例某肿瘤术后病人(采用甲、乙两种治疗方法)随访5年，记录术后生存时间；试绘制生存曲线，并估计两种疗法的生存曲线有无不同。数据见表1，变量包括组别(Group：1=甲疗法组，2=乙疗法组)、结局(Status：1=死亡，0=删失)、随访时间(Time，月)。案例可从“附件下载”处下载。

二、案例分析

本案例分析目的是估计两种疗法的生存曲线有无不同，可考虑使用log-rank检验。但需要满足4个条件：

条件1：结局为互斥的二分类变量，即删失和死亡。该条件满足。

条件2：随访时间或生存时间定义明确，并为量化数据，即以天、周、月、年等为单位的具体数值。本案例数据的生存时间为准确可测量的月数，该条件满足。

条件3：不宜有长期变异存在。对于动态队列，研究对象不是同时进入队列的，那么如果后期进入队列的研究对象使用了新的治疗方案和药物，生存率提高，那么整个队列的生存结果就会发生偏倚。该条件需要根据实际情况来判断，这里默认无长期变异。

条件4：删失事件在各组的分布相似。本案例可根据后文结果进行判断。

三、软件操作及结果结果

(一) 软件操作

1. 数据录入

数据录入，可分为直接输入和外部导入。本案例选择从外部导入。

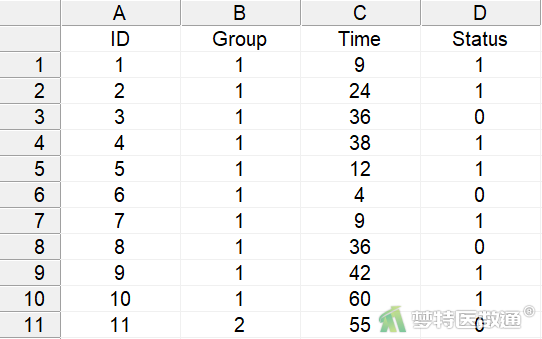
2. 绘制Kaplan-Meier曲线

(1)择“统计”—“生存分析”—“ Kaplan-Meier生存分析”(图2)

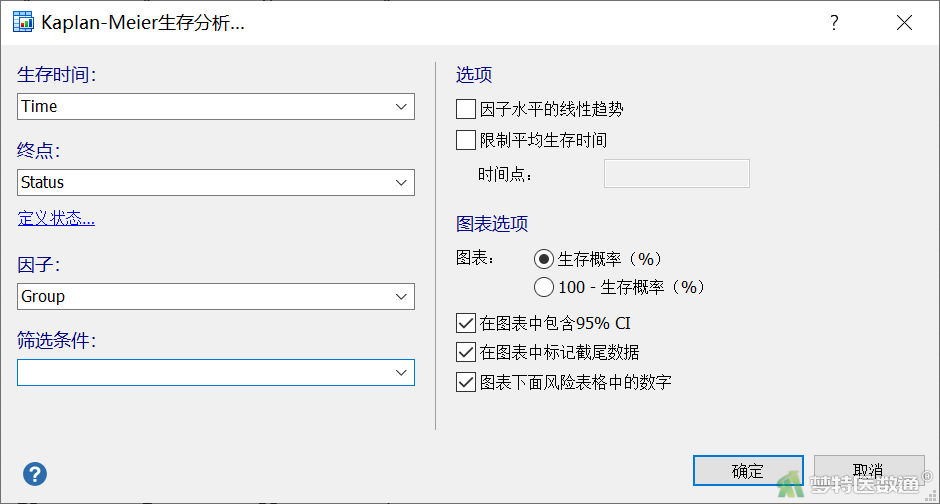
(2) 打开“Kaplan-Meier生存分析”对话框(图3)，各个选项含义参考(单样本生存资料的Kaplan-Meier法)。

• 生存时间：本例为“Time”
• 终点：本例为“Status”，状态是默认值
• 因子：本例为“Group”
• 筛选条件：未选择任何变量
• 选项本例默认选项
• 图表：本例选择“生存概率(%)” “在图表中包含95%CI” “在图表中标记截尾数据” “图表下面风险表格中的数字”

(3) 点击“确定”，得到检验结果

(二) 结果解读

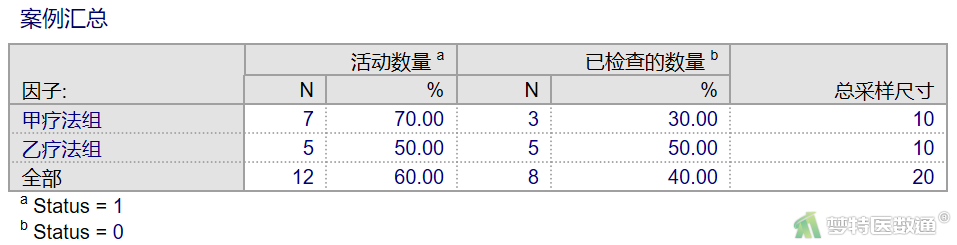
1. 案例汇总

本研究共随访20例某肿瘤术后病人，其中完全数据12例(60%)，删失数据8例(40%)。甲疗法组10人，其中完全数据7例(70%)，删失数据3例(30%)；乙疗法组10人，其中完全数据5例(50%)，删失数据5例(50%)。见图4。

2. 平均和中位生存期

某肿瘤术后病人的平均生存期为37.303月，总体平均生存期的95%CI为(28.064~46.542)月，中位生存期为42.000月，总体中位生存期的95%CI为(18.000~60.000)月。甲疗法组的平均生存期为31.926月，总体平均生存期的95%CI为(18.290~45.562)月，中位生存期为38.000月，总体中位生存期的95%CI为(9.000~60.000)月。乙疗法组的平均生存期为41.770月，总体平均生存期的95%CI为(30.131~53.409)月，中位生存期为43.000月，总体中位生存期的95%CI为(10.000~50.000)月，见图5。所有结果可根据需要保留相应的有效位数

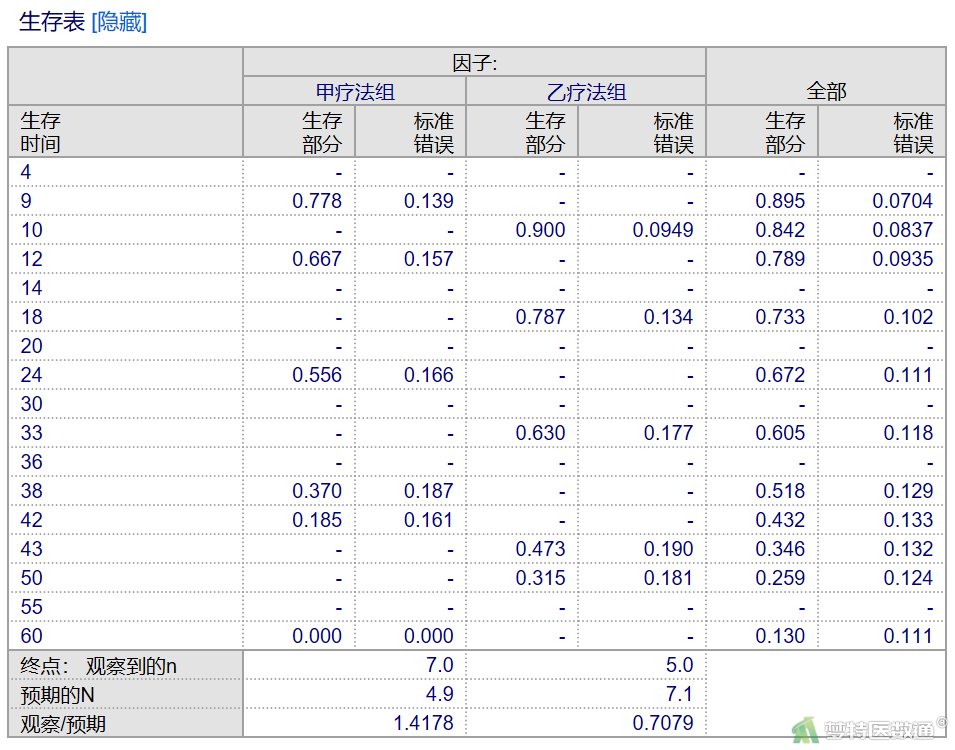
3. 生存表

通过生存表可知，某肿瘤术后病人的总的1年、2年、3年、5年生存率分别约为78.9%、67.2%、60.5%和13.0%；甲疗法组的1年、2年、3年、5年生存率分别约为66.7%、55.6%、55.6%、0%；乙疗法组的1年、2年、3年、5年生存率分别约为90.0%、78.7%、63.0%、31.5%。见图6。

4. log-rank检验结果

Log-rank检验结果为χ²=1.5370，P=0.2151，见图7。按α=0.05水准，拒绝H₀，接受H₁，即甲乙两种疗法的生存曲线相同。

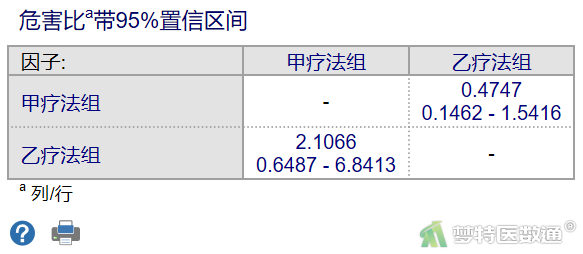
5. 风险比(hazard ratio，HR)

风险比类似于logistic回归中优势比OR值。也体现了相对危险度的概念。即同一时点i时，两组对象的结局风险比。Log-rank检验结果为χ²值有统计学意义时，可以观察HR的大小。HR>1，表示暴露于某因素下死亡风险高(即该因素是危险因素)；HR<1，表示暴露于某因素下死亡风险低(即该因素是保护因素)。当HR的95%CI不包含1时，表示HR与1的差异有统计学意义，包含1时，表示HR与1的差异无统计学意义。甲疗法组与乙疗法组相比，HR=2.1066，95%CI为0.6487~6.8413(乙疗法组与甲疗法组相比，HR=0.4747，95%CI为0.1462~1.5416，不影响统计学推断)，见图8。两组发生死亡风险的差异无统计学意义，与log-rank检验结果相一致。

6. 生存曲线

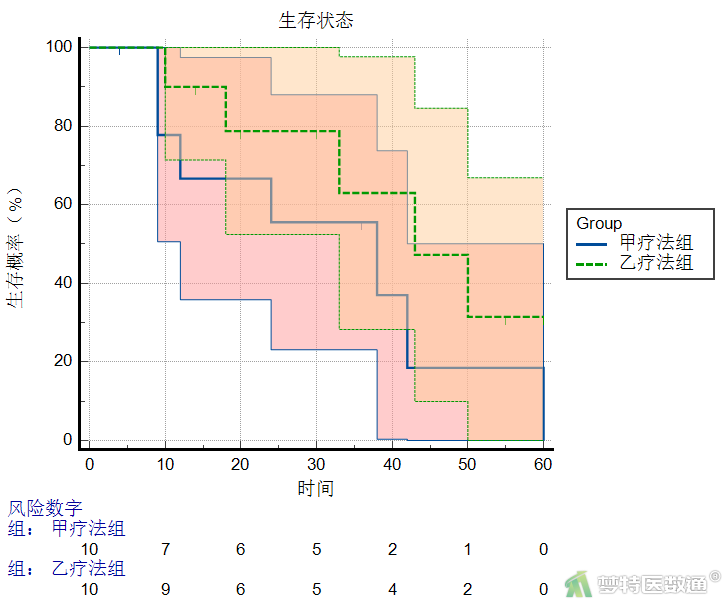
生存曲线上的小垂直线表示删失数据，生存图下方的表格为对应时间的期初暴露人数，生存曲线见图9。根据图9中风险数字可知，该数据满足条件4。结合图5、图7结果，可知乙疗法组生存曲线高于甲疗法组，但两者差异没有统计学意义。

四、结论

本研究采用Kaplan-Meier曲线法绘制生存曲线，并采用log-rank法对不同方法治疗某肿瘤患者的生存结果进行比较。甲、乙疗法组的中位生存期分别为38.0 (95%CI为9.0~60.0)月和43.0 (95%CI为10.0~50.0)月，乙方法高于甲方法，但log-rank检验结果表明两种方法治疗的肿瘤患者生存分布比较，差异无统计学意义(χ²=1.537，P=0.2151)。

五、知识小贴士

(一) 删失数据

在规定的随访期内，未能观察到一些研究对象结局事件的发生，即不能得知结局事件确切的发生时间，称这类研究对象的随访时间/生存时间为删失数据。根据原因可分为3种类型：

(1)研究结束时(已达到规定的最长观察期/随访期)，研究对象仍未出现结局事件；

(2)由于研究对象在研究期间不再继续就诊，或拒绝访视，或失去联系等，未能观察到结局事件；

(3)研究对象出现了竞争事件(如其他原因的死亡)，观察不到既定的结局事件而终止随访。

(二) 中位生存时间

中位生存时间表示累积生存率为50%所对应的时间，是生存分析中最常用的描述性统计量。生存分析中较少使用平均生存时间。

(三) Log-rank检验

Log-rank检验中的“log”并非为“对数”，而是表示“count”、“register”或“record”。在中文描述中可以直接写为“log-rank检验”，或者译为“时序检验”。

Log-rank检验是比较不同组患者生存曲线的非参数检验，属于单因素分析。若想校正其他因素则需要采用Cox比例风险模型进行分析。