R×C卡方检验—理论介绍中提到,当多个样本率比较的R×C表资料χ²检验,推断结论为拒绝H0,接受H1时,只能认为各总体率之间整体比较有差异,但尚不能说明任意两个总体率之间都有差别。若要进一步推断具体哪两个总体率有差别,若直接用四格表资料的χ²检验进行多重比较,将会加大犯I型错误的概率。多个样本率间多重比较的方法有 χ²分割法(partitions of χ² method、Scheffé置信区间法和SNK法。本文介绍调整检验水准的Bonferronir χ²分割法和Scheffé置信区间法。
关键词:多个率比较; 事后检验; 两两比较; 卡方分割法; Scheffé置信区间法
一、基本思想
多个样本率比较的资料可整理成2×k表资料,经行×列表资料χ²检验的结论为拒绝H0,接受H1时,若不经过任何处理,而直接用分割法把2×k表χ²分成多个独立的四格表χ²进行两两比较,须重新设定检验水准,目的是为保证检验假设中I型错误α的概率不变。
(一) χ²分割Sidak法
将多个样本率比较的列联表资料经两两分割,整理成多个四格表的形式。如果有k个组,将分割出\(m=C_{k}^{2}=\frac{k(k-1)}{2}\)个四格表,进行m次检验。
1.检验水准a'的计算
为保证假设检验时犯I型错误的总概率α不变,根据Sidak法的思想,每次比较的检验水准须为
\( \alpha^{\prime}=1-\sqrt[m]{1-\alpha}\)
2.检验统计量χ²的计算
\(\chi^{2}=\frac{(a d-b c)^{2} n}{(a+b)(c+d)(a+c)(b+d)}\)
(二) Scheffé置信区间法
该法依据Scheffé法的多重比较原理,通过计算两率之差的置信区间来推断比较组间有无差异。两率之差的100 (1-α) %置信区间按下式计算:
\(\left(p_{A}-p_{B}\right) \pm \sqrt{\chi_{\alpha, k-1}^{2}\left[\frac{p_{A}\left(1-p_{A}\right)}{n_{A}}+\frac{p_{B}\left(1-p_{B}\right)}{n_{B}}\right]}\)
式中,pA和pB分别为两个比较组的样本率;nA和nB分别为两个比较组的样本含量;k为所有的组数。
二、案例数据
某科室回顾性研究推拿疗法、药物疗法和针灸疗法3种疗法治疗腱鞘炎的疗效,数据见图1。问3种疗法中是否任意两种疗法治疗腱鞘炎的有效率均有差别?
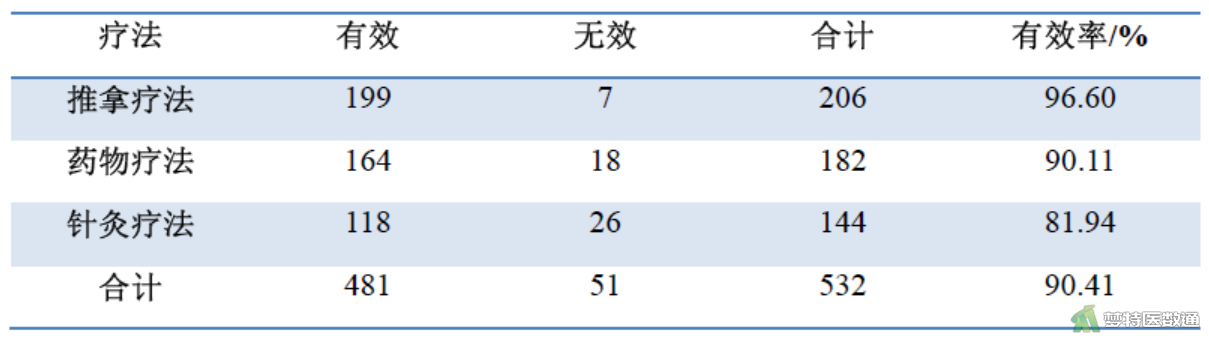
三、两两比较
(一) Sidak法
1. 建立检验假设,确定检验水准
H0:πA=πB,即任意两组的总体有效率相等
H1:πA≠πB,即任意两组的总体有效率不等
α=0.05
本案例为3个组之间的两两比较,比较次数 \(m=C_{3}^{2}=\frac{3(3-1)}{2}=3 \) ,可以分割出3个四格表,进行3次检验。因此,校正检验水准为:
\(\alpha^{\prime}=1-\sqrt[m]{1-\alpha}=1-\sqrt[3]{1-0.05}=0.017, \quad v=1\)
2. 计算检验统计量
(1) 推拿疗法与药物疗法之间的比较
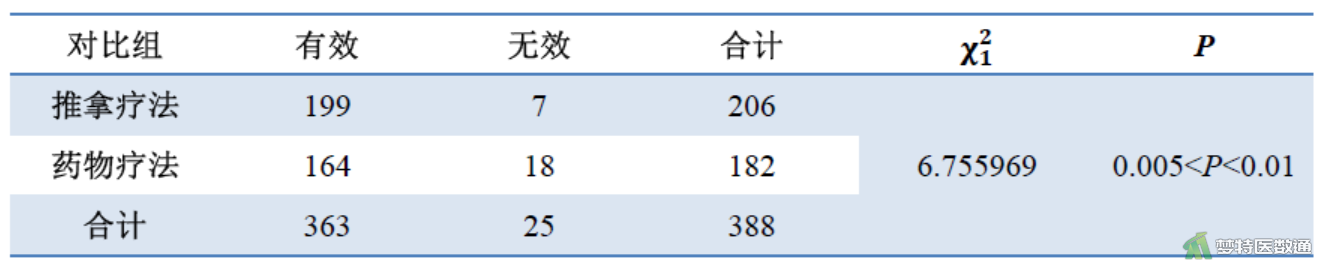
\(\chi_{1}^{2}=\frac{(a d-b c)^{2} n}{(a+b)(c+d)(a+c)(b+d)}=\frac{(199 \times 18-164 \times 7)^{2} \times 388}{(199+7)(164+18)(199+164)(7+18)}=6.755969\)
(2) 推拿疗法与针灸疗法之间的比较

\(\chi_{2}^{2}=\frac{(a d-b c)^{2} n}{(a+b)(c+d)(a+c)(b+d)}=\frac{(199 \times 26-118 \times 7)^{2} \times 350}{(199+7)(118+26)(199+118)(7+26)}=21.322798\)
(3) 药物疗法与针灸疗法之间的比较

\(\chi_{3}^{2}=\frac{(a d-b c)^{2} n}{(a+b)(c+d)(a+c)(b+d)}=\frac{(164 \times 26-118 \times 18)^{2} \times 326}{(164+18)(118+26)(164+118)(18+26)}=4.591023\)
3. 确定P值,作出推断结论
按ν=1查(χ²界值表)\(\chi_{0.01}^{2}\)=6.63,\(\chi_{0.005}^{2}\)=7.88;因6.63<6.755969<7.88,故0.005<P<0.01。按α'=0.017检验水准,推拿疗法组和药物疗法组拒绝H0,接受H1,可认为推拿疗法和药物疗法的总体有效率有差别。同理可得,推拿疗法组和针灸疗法组拒绝H0,接受H1,可认为推拿疗法和针灸疗法的总体有效率有差别。药物疗法组和针灸疗法组不拒绝H0,还不能认为药物疗法和针灸疗法的总体有效率有差别。综上所述,可认为推拿疗法的有效率高于其他两种疗法,但还不能认为药物疗法和针灸疗法的有效率有差别。
(二) Scheffé法
1. 计算置信区间
计算“推拿疗法”和“药物疗法”总体有效率之差的95%置信区间如下(\(\chi_{0.05,3-1}^{2}=5.99\)):
\((0.966-0.9011)\pm\sqrt{5.99\times\left[\frac{0.966\times(1-0.966)}{206}+\frac{0.9011\times(1-0.9011)}{182}\right]}\)
即(0.002789,0.127010)。同理,可算得其他疗法之间有效率之差的95%置信区间,结果见图5。
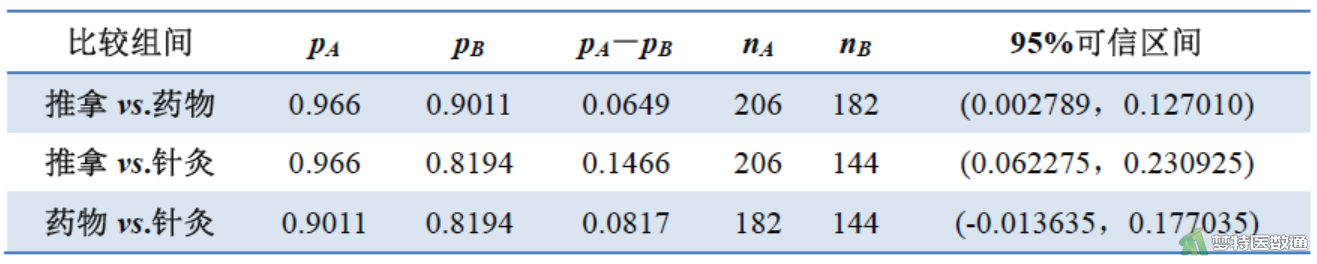
1. 作出推断结论
采用Scheffé法进行率的多重比较可见,推拿疗法和药物疗法两组有效率差异的置信区间不包含0,表明两法总体有效率之间差异有统计学意义;同理,推拿疗法和针灸疗法两组有效率差异的置信区间不包含0,表明两法总体有效率之间差异有统计学意义;药物疗法和针灸疗法两组有效率差异的置信区间包含0,表明两法总体有效率之间差异无统计学意义。