稳健线性回归分析(Robust Linear Regression Analysis)——Stata软件实现

关键词：Stata; 稳健线性回归; 离群值; 线性回归; Robust regresson

一、案例介绍

某医生从电子病例系统收集了122例高血压患者的Age (年龄，岁)、Sex (性别：1=男，2=女)、Smoke (吸烟：0=不吸烟，1=吸烟)、LDL-C (低密度脂蛋白胆固醇，mmol/L)、UA (尿酸，μmol/L)、Hcy (同型半胱氨酸，μmol/L)和SSD_24h (24小时收缩压标准差)，拟探究高血压患者24小时收缩压标准差的影响因素。部分数据见图1。案例可从“附件下载”处下载。

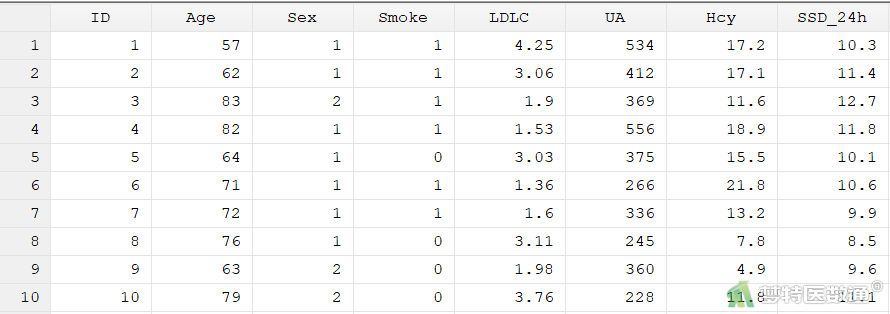
二、问题分析

本案例的分析目的是探究高血压患者24小时收缩压标准差的影响因素，即Age、Sex、Smoke、LDL-C、UA、Hcy对SSD_24h的影响。在案例中，SSD_24h为连续性变量，可考虑进行线性回归分析。根据临床经验，24小时收缩压标准差的测量值中可能存在离群值。因此，可使用稳健估计方法估计线性回归系数，即使用稳健线性回归分析的影响因素。但需要满足3个主要重要条件：

条件1：因变量为连续性变量。SSD_24h为连续性变量，满足该条件。

条件2：因变量服从正态或近似正态分布，该条件需要通过软件分析后判断。

条件3：因变量中存在离群值或强影响点，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 数据整理

1. 添加变量标签

使用label variable varname ["label"]为各变量添加中文标签。

label variable Age "年龄"
label variable Sex "性别"
label variable Smoke "吸烟"
label variable LDLC "低密度脂蛋白胆固醇"
label variable UA "尿酸"
label variable Hcy "同型半胱氨酸"
label variable SSD_24h "24小时收缩压标准差"

2. 添加数值(水平)标签

使用label define lblname # "label" [# "label" ...]为分类变量添加数值标签。

label define Sex 1 "男" 2 "女"
label define Smoke 0 "不吸烟" 1 "吸烟"

3. 查看、显示标签

完成标签添加后，可在变量窗口中查看(图2)，或通过命令des进行查看，见图3。

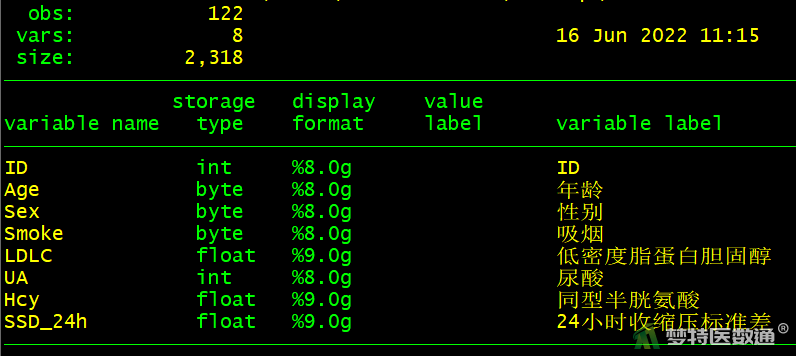
(二) 适用条件判断

1. 条件2判断(正态性检验)

(1) 软件操作

① Shapiro-Wilk正态性检验

swilk SSD_24h

② 绘制Q-Q图

qnorm SSD_24h

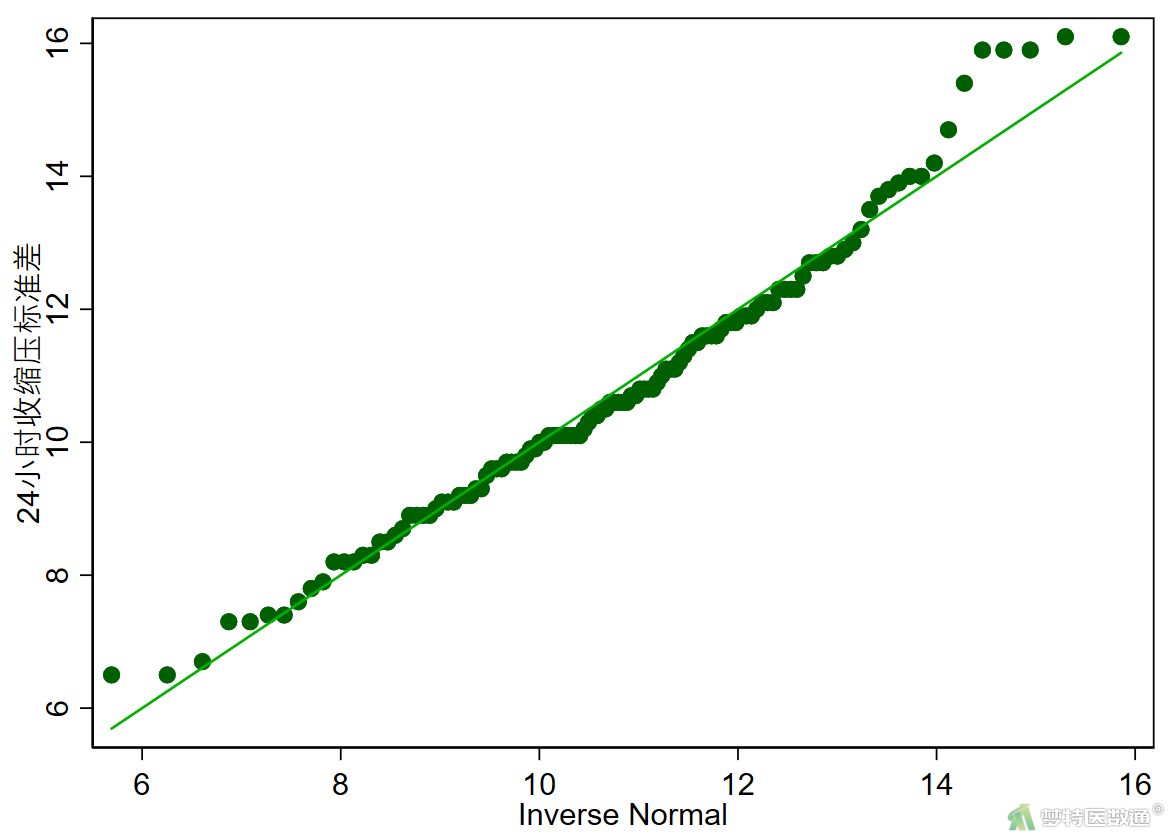
③ 绘制直方图

histogram SSD_24h, bin(15)

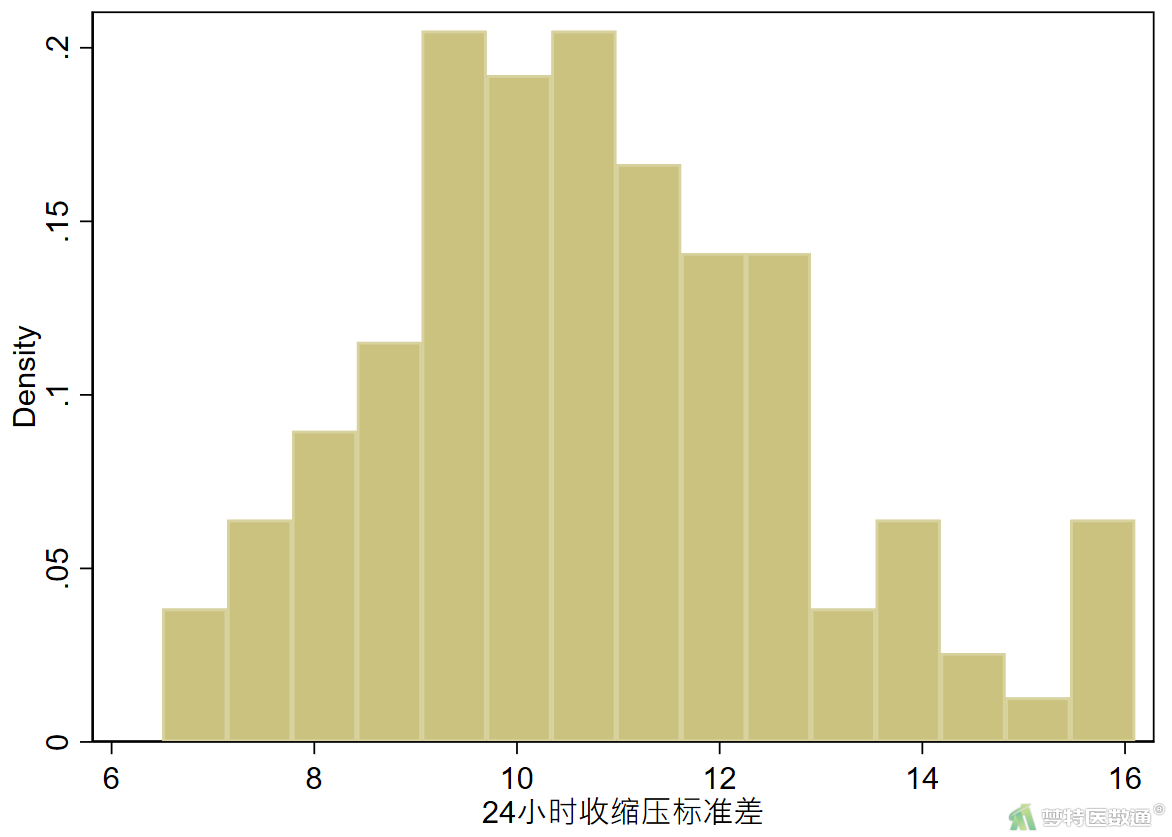
(2) 结果解读

图4中正态性检验结果显示，P=0.078>0.05，可认为服从正态分布；图5和图6也提示数据近似服从正态分布。综上，可认为SSD_24h满足正态性。

2. 条件3判断(离群值/强影响点)

(1) 软件操作

① 对SSD_24h进行描述性分析

summarize SSD_24h, detail

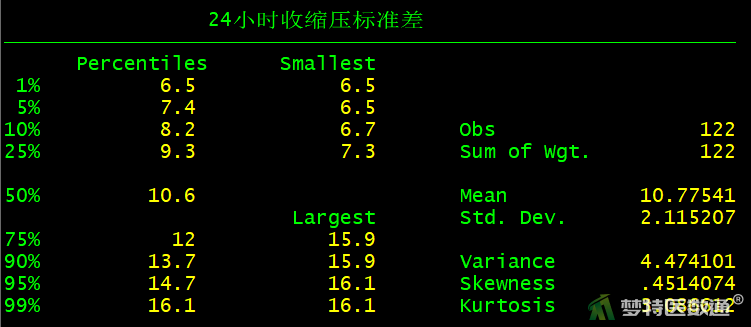
② 绘制箱线图

graph box SSD_24h

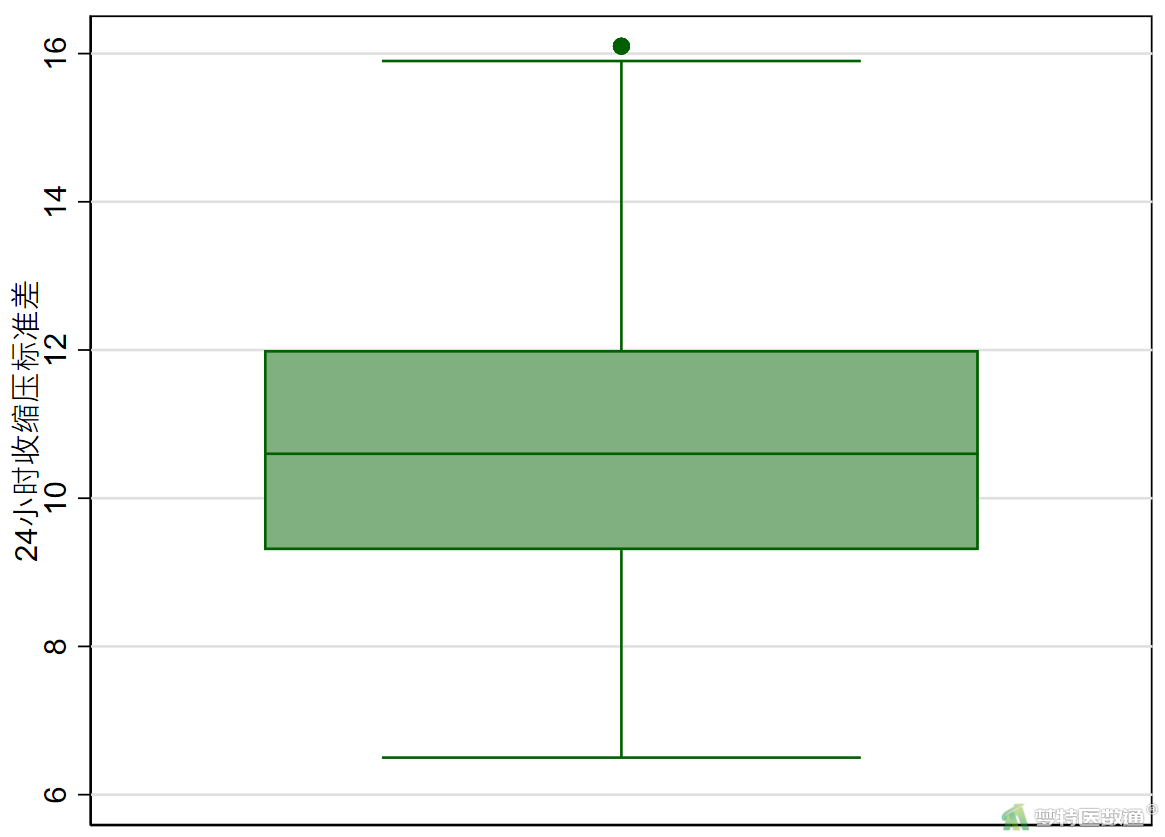
③ 查看杠杆值

拟合OLS线性回归(图9)

reg SSD_24h Age i.Sex i.Smoke LDLC UA Hcy

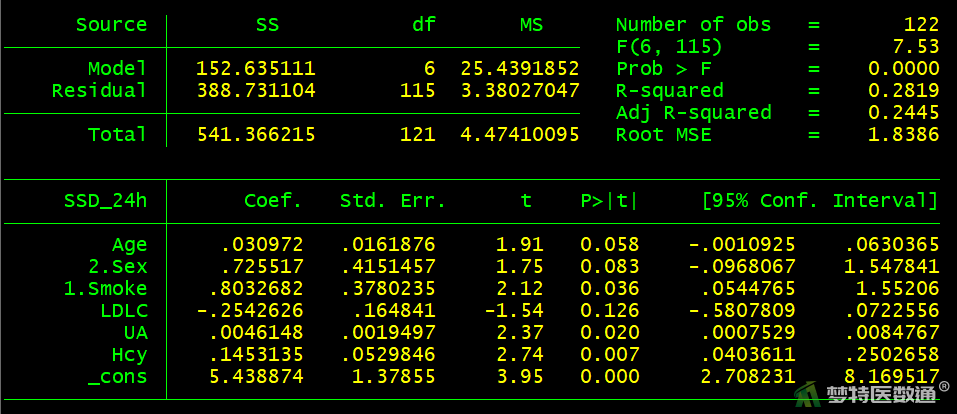
绘图

lvr2plot, mlabel(ID)

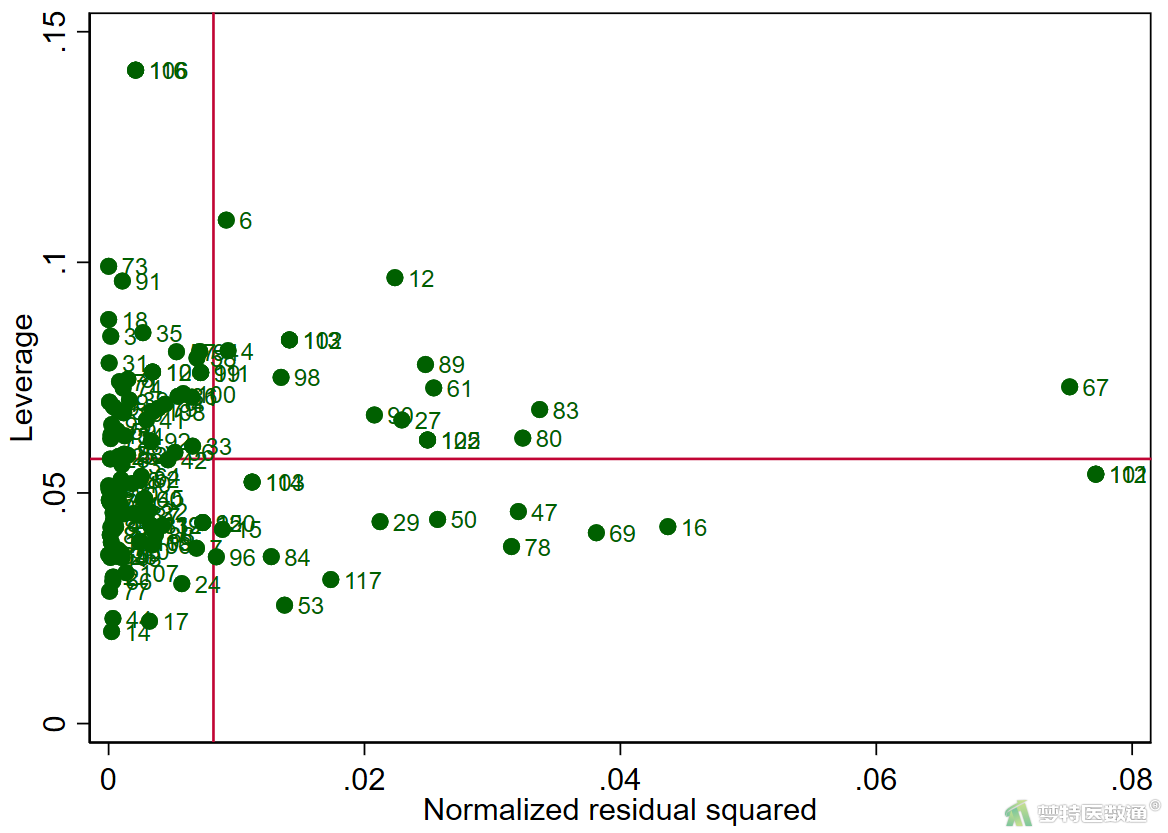
(2) 结果解读

图7中显示了SSD_24h的描述性分析结果，可知最大值为16.1，结合图8中的箱线图可知，因变量SSD_24h中存在个别离群值。图10给出了模型诊断结果，横轴为标准化残差平方，纵轴为杠杆值，可知存在个别高杠杆值(如，ID: 106)和标准残差平方较大的观测(如，ID: 67、102)。

(三) 变量筛选

1. 软件操作

由于本案例中存在个别离群值以及高杠杆值，因此可以使用稳健线性回归进行模型拟合。先使用单因素稳健线性回归进行变量筛选

* 年龄 *

rreg SSD_24h Age

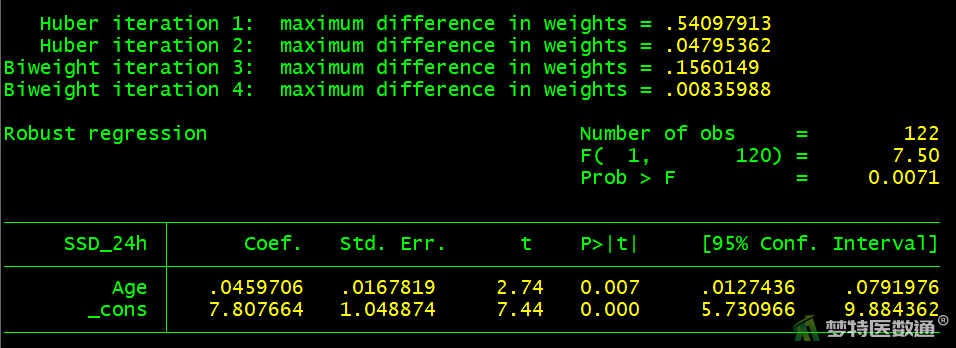
* 性别 *

rreg SSD_24h i.Sex

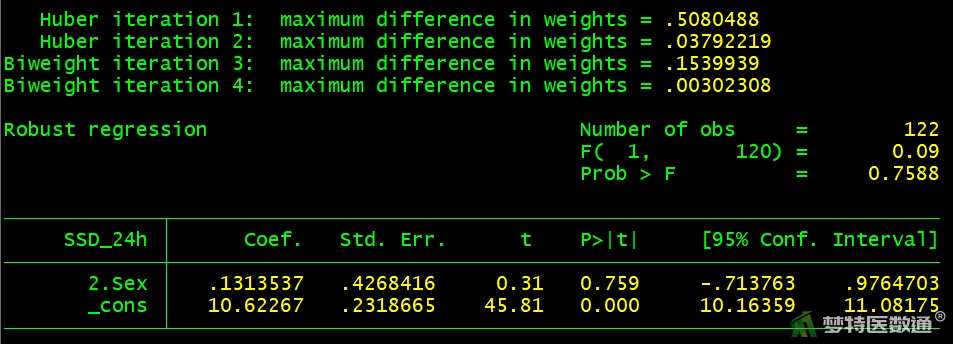
* 吸烟 *

rreg SSD_24h i.Smoke

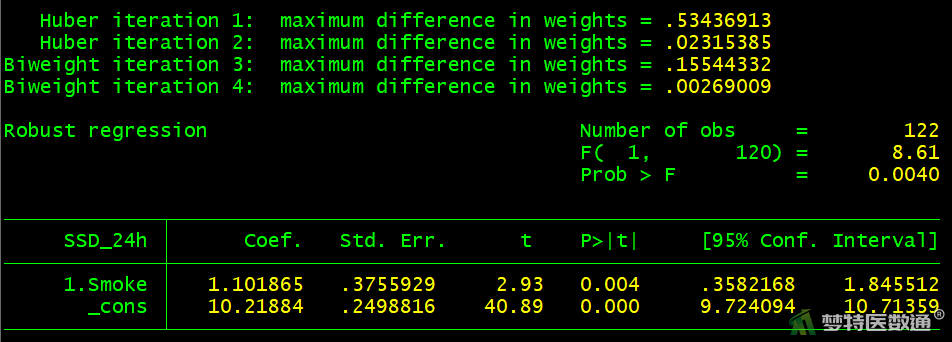
* 低密度脂蛋白胆固醇 *

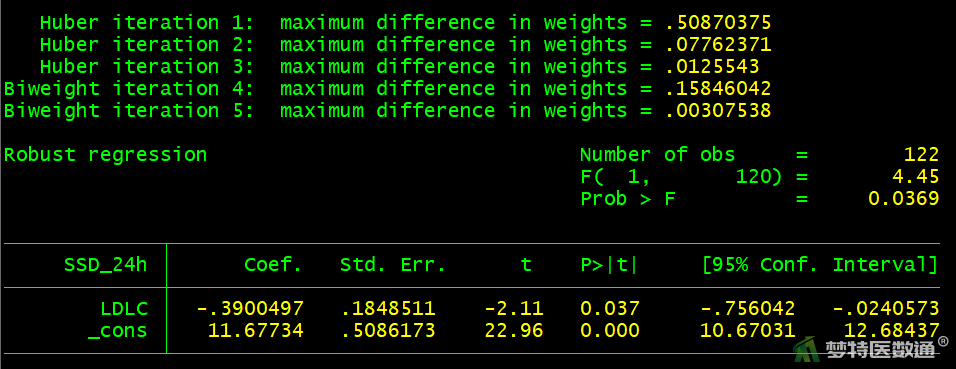
rreg SSD_24h LDLC

* 尿酸 *

rreg SSD_24h UA

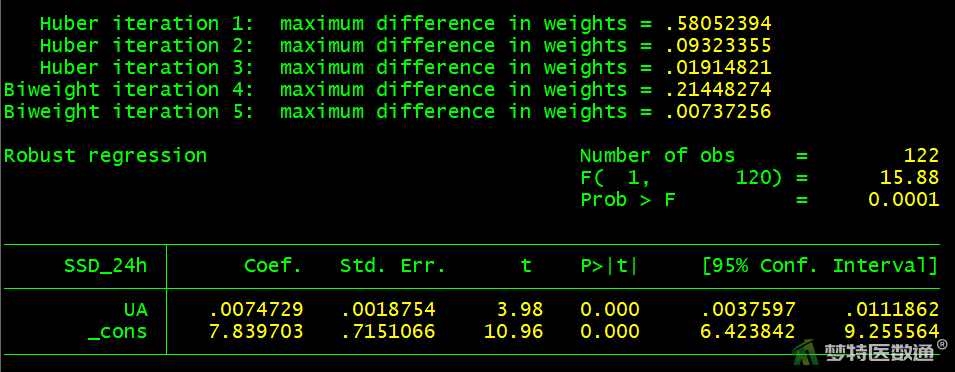
* 同型半胱氨酸 *

rreg SSD_24h Hcy

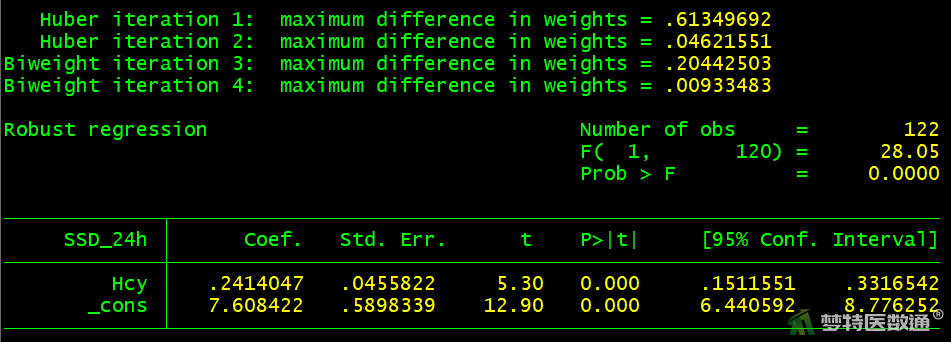
2. 结果解读

图11~16给出单因素回归的结果，结果显示年龄、吸烟、低密度脂蛋白胆固醇、尿酸、同型半胱氨酸在模型中有统计学意义(P<0.05)，性别在模型中无统计学意义(P>0.05)。即单因素结果显示年龄、吸烟、低密度脂蛋白胆固醇、尿酸、同型半胱氨酸与24小时收缩压标准差的关联有统计学意义。

(四) 模型拟合

根据变量筛选结果，可以将年龄、吸烟、低密度脂蛋白胆固醇、尿酸和同型半胱氨酸纳入到多因素稳健线性回归中，探究24小时收缩压标准差的影响因素。

1. 软件操作

 * 多因素回归 *

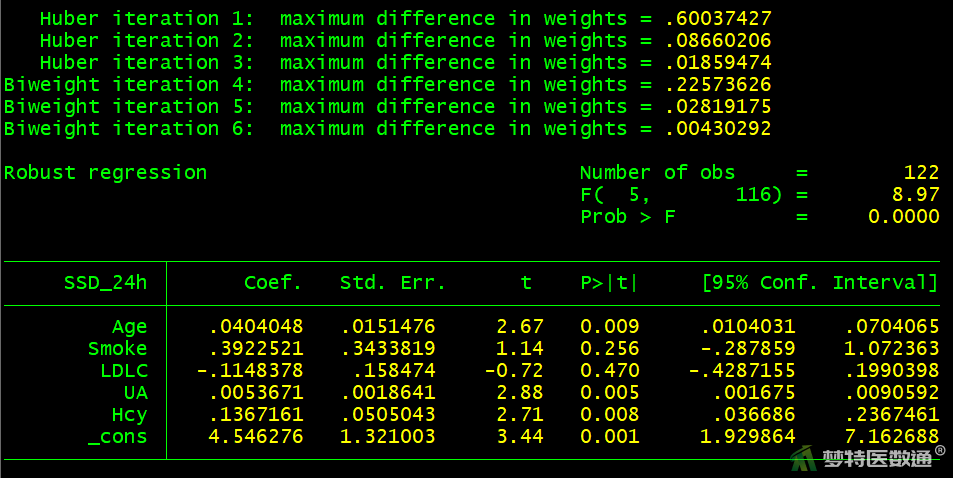
rreg SSD_24h Age Smoke LDLC UA Hcy

* 模型拟合评价 *

rregfit

rregfit模块非软件自带，使用前需要先安装。详见Stata外部命令的下载与安装。

2. 结果解读

(1) 模型拟合

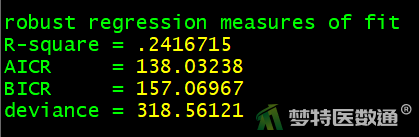
图17给出了模型整体评价的结果，可知F=8.97，P<0.001，表明模型整体有统计学意义(至少有一个变量在模型中有统计学意义)。图18给出了模型评价结果，可知决定系数R²=0.242，模型能解释24小时收缩标准差总变异的24.2%。

(2) 变量系数

图17给出了多因素稳健线性回归的结果，年龄、尿酸和同型半胱氨酸与24小时收缩压标准差的关联有统计学意义(P<0.05)，吸烟、低密度脂蛋白胆固醇与24小时收缩压标准差的关联无统计学意义(P>0.05)。其中，年龄每增加1岁，24小时收缩压标准差升高0.04；尿酸每升高一个单位，24小时收缩压标准差升高0.005；同型半胱氨酸每上升一个单位，24小时收缩压标准差升高0.137。

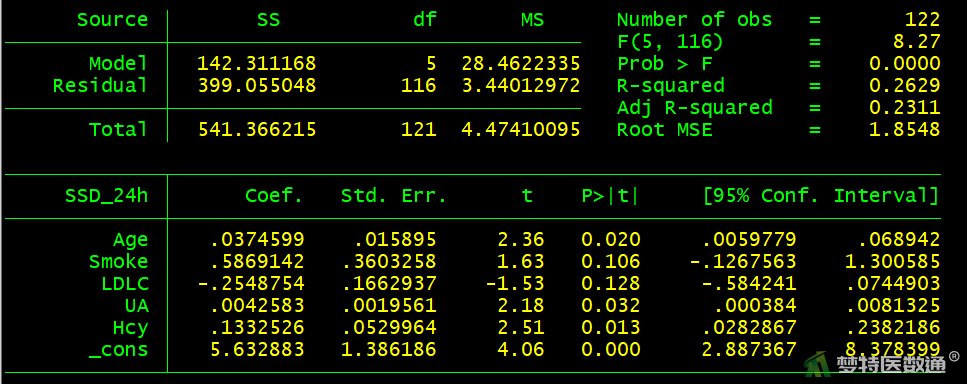
如果本案例使用OLS分析(代码如下)，结果如图19所示。

reg SSD_24h Age Smoke LDLC UA Hcy

与稳健回归分析结果对比可知尽管关联有统计学意义的变量未发生改变，但是变量的回归系数并不一样。

四、结论

本案例采用稳健线性回归分析了年龄、性别、吸烟、低密度脂蛋白胆固醇、尿酸、同型半胱氨酸对24小时收缩压标准差的影响。因变量为连续性变量，服从正态分布，因变量中存在离群值，存在高杠杆值的观测，满足主要的应用条件。

多因素模型通过整体检验，有统计学意义(F=8.97，P<0.001)，决定系数R²=0.242，模型能解释24小时收缩标准差总变异的24.2%。

多因素分析结果显示，年龄、尿酸和同型半胱氨酸是24小时收缩压标准差的影响因素。其中，年龄每增加1岁，24小时收缩压标准差升高0.04；尿酸每升高一个单位，24小时收缩压标准差升高0.005；同型半胱氨酸每上升一个单位，24小时收缩压标准差升高0.137。

五、知识小贴士

• 稳健估计方法

稳健估计的方法主要包括：基于迭代加权最小二乘法的M估计，基于残差秩次的R估计，基于最小平方中位数的LMS估计，及S估计、MM估计等。这些估计方法的整体思想均是为了消除离群值/异常点/影响点对回归拟合的影响。

• 命令rreg是基于M估计对线性回归的回归系数进行稳健估计，其主要思想是根据回归残差的大小确定各个观测的权重，再进行迭代最小二乘法估计，即迭代加权最小二乘法。M估计只能克服来源于因变量的异常点，不能克服来源于自变量的异常点。
• MM估计是基于M估计和S估计的思想建立起来的稳健估计方法，可以克服来源于自变量的异常点/高杠杆值，也可以克服来源于因变量的异常点。其基本思想是先通过迭代的S估计得到稳健的初始估计值，再通过M估计求出回归系数。

六、分析小技巧

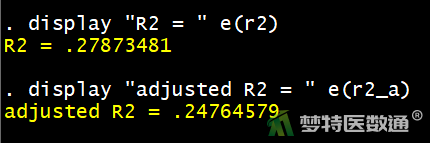
• 模型的R²与adjusted R²

在进行稳健线性回归后，可以使用display "R2 = " e(r2)和display "adjusted R2 = " e(r2_a)给出模型拟合的R²与adjusted R²。但这两个数值是基于OLS回归得出的，是错误的。如图18，所得R²与使用rregfit命令所得的结果不一致。命令rregfit是由加州大学洛杉矶分析编写的程序 (首次使用前需要先进行安装，可以通过命令findit rregfit或者search rregfit搜索程序，并找到相应链接进行安装)，可以计算R²和其他几个评价指标。

• 其他命令

根据稳健估计方法不同，研究人员开发出了不同的执行稳健线性回归的命令，常见的有mregress 和 mmregress，他们分别是基于M估计和MM估计开发而来。