两因素方差分析(Two-way ANOVA)一(无交互作用)——MedCalc软件实现

关键词：MedCalc; 两因素方差分析; 交互作用; 主效应; 单独效应; 简单效应

一、案例介绍

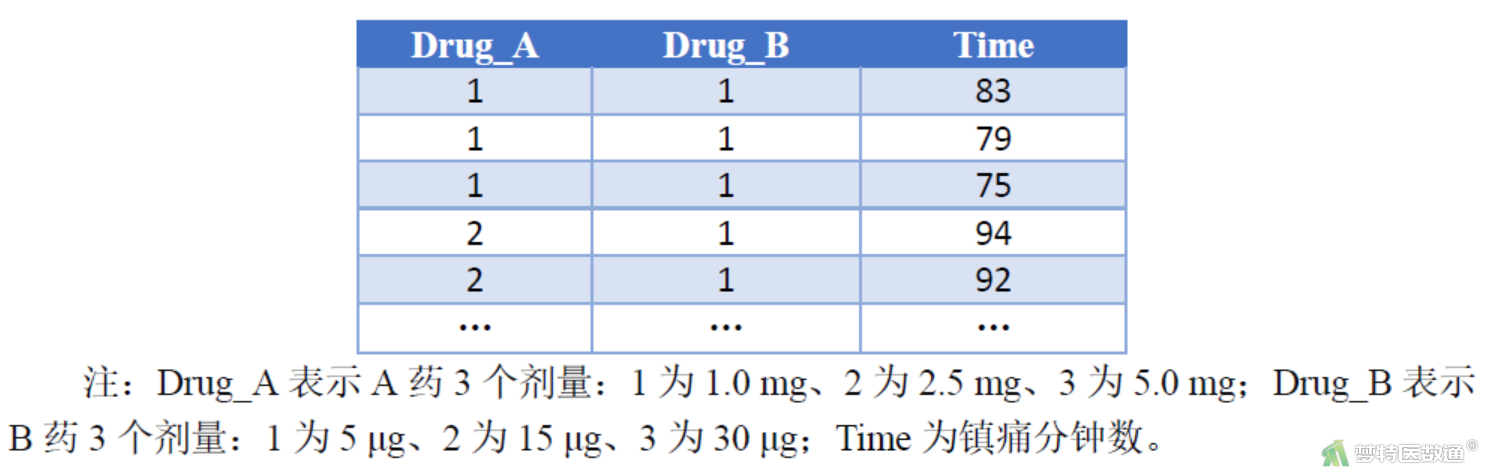
研究A、B两种镇痛药物联合运用在癌症患者的镇痛效果。A药取3个剂量：1.0、2.5、5.0 mg；B药也取3个剂量：5、15、30 μg，共9个处理组。将27例研究对象随机分成9组，每组3例，记录每名对象的镇痛时间Time (min)。试分析A、B两药联合运用的镇痛效果。部分数据见图1，案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是分析A、B两药联合运用的镇痛效果。临床上，药物之间联合运用往往会相互影响，这种影响可能为正向的增强效应，也可能为反向的拮抗作用。针对这种情况，可以使用多因素方差分析。由于本案例为药物A和药物B两个因素，因此可以使用两因素方差分析。但需要满足6个条件：

条件1：观察变量唯一，且为连续变量。本研究中观察变量只有镇痛时间，且为连续变量，该条件满足。

条件2：有两个因素，且都为分类变量。本研究中有药物A、药物B两个因素，都为分类变量，该条件满足。

条件3：观测值相互独立。本研究中各研究对象的观测值都是独立的，不存在互相干扰的情况，该条件满足。

条件4：观察变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件5：各组、各水平观测值为正态(或近似正态)分布，因为本案例中每个组的观察数较少，所以需要使用残差检验整体的正态性。该条件需要通过软件分析后判断。

条件6：相互比较的各处理水平(组别)的总体方差相等，即方差齐同，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一)数据准备

• 打开MedCalc软件，导入数据如图2所示。

• 点击左侧“变量”，出现“变量”对话框，在此处选中需要进行标签设置的变量后点击右侧“属性”(图3)即可出现“变量属性”对话框。

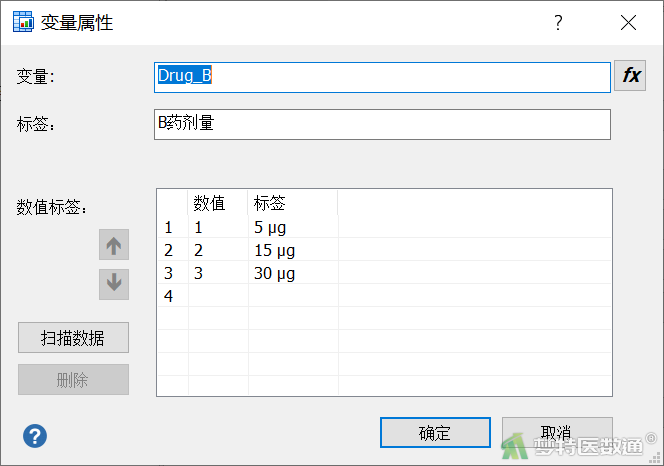
• 在“变量属性”对话框中设置变量“Drug_A”和“Drug_B”的标签，如图4-1和图4-2所示。

(二)适用条件判断

条件4-6的判断均需要根据方差分析生成的残差进行分析，详见下文“方差分析”部分。

(三) 方差分析

1. 生成模型残差

• 选择“统计”—“方差分析”—“方差双向分析...”(图5)。

• 在“方差双向分析”对话框中，“从属数据”中选择“Time”,“因子A”中选择“Drug_A”，“因子B”中选择“Drug_B”，其他保持默认不变，点击“确定”(图6)。

• 在分析结果最右下角点击“保存残差”，出现图7页面，“选项”下勾选“标准化”，点击确定。在数据视图页面可见生成了一列新的变量“ANOVA_Resid1”，即为模型的标准化残差(图8)。

2. 适用条件判断

(1) 条件4判断(异常值检测)

选择“统计”—“异常值检测”(图9)；将“ANOVA_Resid1”选入“变量”，其他设置见图10；结果如图11所示。

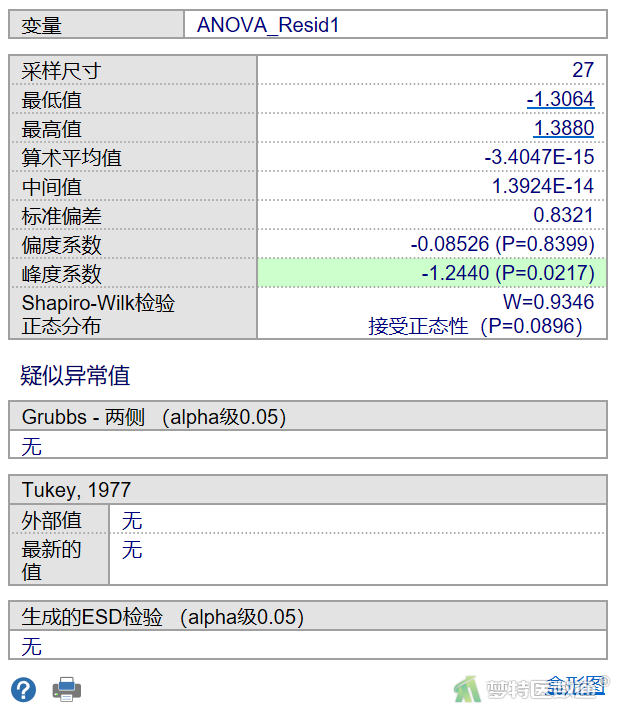
图11为残差的异常值检测结果，可见未发现异常值。

(2) 条件5判断(正态性检验)

图12为残差正态性检验结果：W=0.935，P=0.090，按α=0.05水准，接受正态性，满足条件5。

(3) 条件6判断(方差齐性检验)

图13为误差方差齐性检验结果：F=0.304，P=0.955，按α=0.10水准，拒绝H₀，可以认为总体方差齐，满足条件6。

3. 统计描述结果

图14为不同药物A剂量和药物B剂量下，镇痛效果的描述：药物A在1.0 mg水平，药物B为5、15、30 μg水平时，镇痛时间分别为：79.00、94.33、108.67 min；药物A在2.5 mg水平，药物B为5、15、30 μg水平时，镇痛时间分别为：90.67、106.67、116.67 min；药物A在5.0 mg水平，药物B为5、15、30 μg水平时，镇痛时间分别为：108.00、118.33、132.00 min。

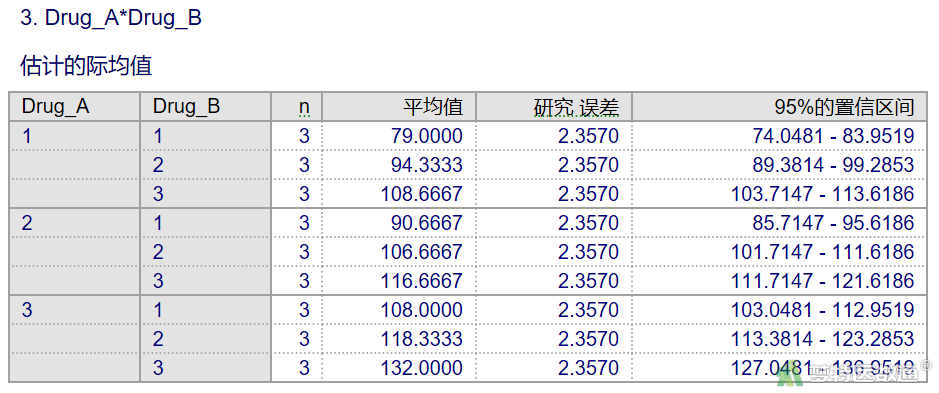
4. 交互作用判断

点击图12右下方“多重对比图”，在图15“集群多重对比图表”页面，“数据”下选择“Time”，“因子代码”下选择“Drug_A”，“按因子定义集群”下选择“Drug_B”，“图表”下勾选“连接线”。A、B药物不同剂量下镇痛时间图示化结果如图16所示，可见随着A药浓度的增加，镇痛时间逐渐上升；随着B药浓度的增加，镇痛时间也逐渐上升；并且增加的幅度基本保持一致。提示两药物之间可能不存在交互作用，但还需要依据统计学推断的结果进行判断。

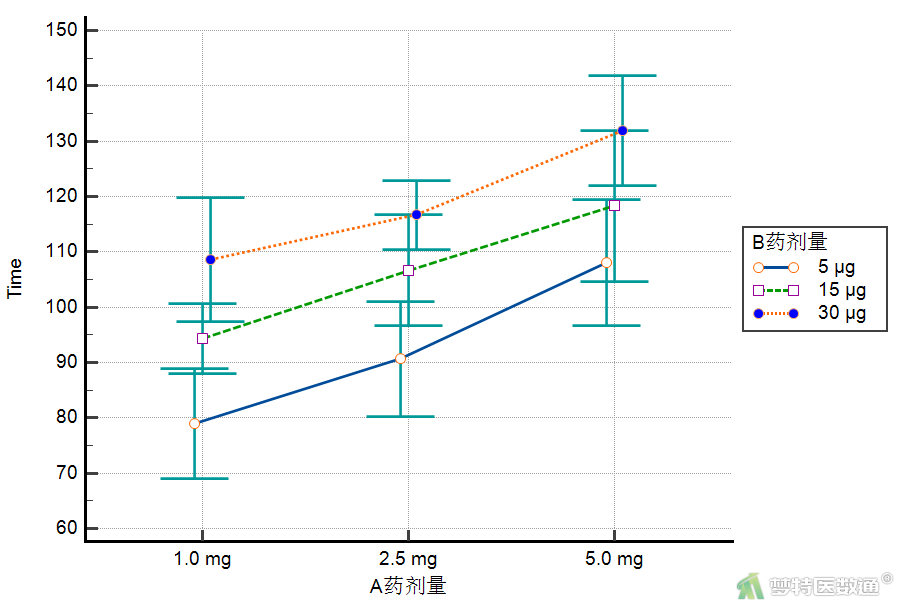
图17为方差分析结果：第三行数据显示了药物A与药物B的交互效应：F=0.699，P=0.603，无统计学意义，尚不能认为药物A和药物B有交互效应。所以可以直接看主效应，药物A：F=88.162，P<0.001，药物B：F=95.269，P<0.001。差异均有统计学意义，可以认为药物A和药物B对镇痛均有影响。

5. 事后检验(两两比较)

以上分析结果显示药物A和药物B对镇痛均有影响，需进一步分别对药物A和药物B进行两两比较。

图18显示药物A三个剂量水平的均值分别为94.00、104.67、119.44 min。图19为药物A三个剂量组的两两比较结果，任意两组比较均P<0.05。可知，2.5 mg和5.0 mg与1.0 mg相比，均值差逐渐增大。2.5 mg比1.0 mg时均值增加了10.67 min，至5.0 mg时增加了25.44 min，2.5 mg到5.0 mg时均值增加了14.78 min，差异均有统计学意义(P<0.001)。以上结果表明，随着A药药物浓度的增加，镇痛时间呈上升趋势。

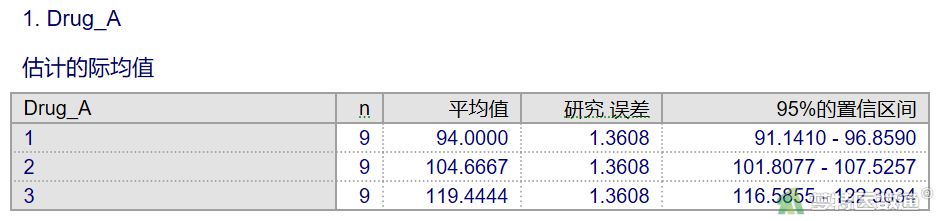
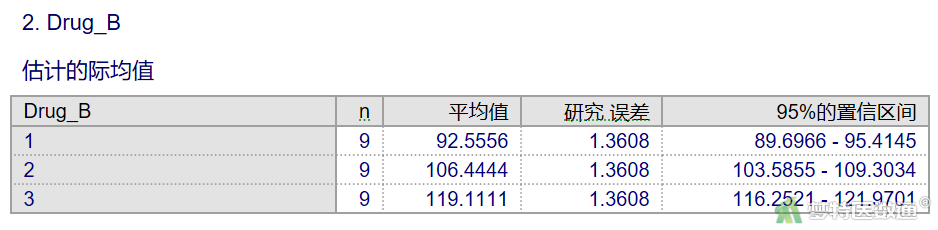
图20显示药物B三个剂量水平的均值分别为92.56、106.44、119.11 min。图21为药物B三个剂量组的两两比较结果，任意两组比较的P值均小于0.05。可知，15.0 μg和30.0 μg与5.0 μg相比，均值差逐渐增大。15.0 μg比5.0 μg时均值增加了13.89 min，至30.0 μg时增加了26.56 min，15.0 μg到30.0 μg时均值增加了12.67 min，差异均有统计学意义(P<0.001)。以上结果表明，随着B药药物浓度的增加，镇痛时间呈上升趋势。

四、结论

本研究采用两因素方差分析探讨A、B两种镇痛药物联合运用在癌症患者的镇痛效果。数据不存在异常值，残差服从正态分布，总体方差齐同；通过两因素方差分析发现两药物之间无交互作用(F_{Drug_A*Drug_B}=0.699，P=0.603)，所以重点看药物A和药物B的主效应。

药物A在1.0 mg水平，药物B为5、15、30 μg水平时，镇痛时间分别为：79.00、94.33、108.67 min；药物A在2.5 mg水平，药物B为5、15、30 μg水平时，镇痛时间分别为：90.67、106.67、116.67 min；药物A在5.0 mg水平，药物B为5、15、30 μg水平时，镇痛时间分别为：108.00、118.33、132.00 min。药物A的主效应检验结果为，F_{Drug_A}=88.162，P<0.001，认为不同药物A浓度时，镇痛时间差异有统计学意义。药物B的主效应检验结果为，F_{Drug_B}=95.269，P<0.001，认为不同药物B浓度时，镇痛时间差异有统计学意义。

进一步采用“Bonferroni”校正法进行同一药物不同剂量组之间的两两比较，可知药物A 2.5 mg和5.0 mg与1.0 mg相比，均值差逐渐增大，差异均有统计学意义(P<0.001)；表明：随着药物A物浓度的增加，镇痛时间呈上升趋势。药物B 15.0 μg和30.0 μg与5.0 μg相比，均值差逐渐增大，差异均有统计学意义(P<0.001)。表明：随着药物B物浓度的增加，镇痛时间呈上升趋势。

综上可知，不同剂量药物A的镇痛效果不同，不同剂量药物B的镇痛效果不同，A、B两种药物不存在交互作用。

五、分析小技巧

• 正态性检验：两因素或多因素方差分析时，有两种选择来测试正态性。如果每组有较多观察数，且组别较少时，可使用原始数据检查每个组的正态性；如果有很多组，或每个组的观察数很少，可使用残差检查整体的正态性。
• 交互作用判断：两因素方差分析时，需要首先判断两个因素之间是否存在交互作用。如果交互作用有统计学意义，则需要分析单独效应。此时，单纯研究某个因素的作用并无意义，应分别探讨另一个因素不同水平时对该因素的作用。当不存在交互作用时，说明两因素的作用彼此独立，逐一分析各因素的主效应即可。