为何配对卡方检验结果不那么可信？

关键词：诊断试验; 配对卡方检验;配对四格表; McNemar检验

在深入了解配对四格表的卡方检验之前，先回顾其基本概念。配对研究是用于比较结果资料为二分类的两种检验方法、培养方法或诊断方法等的差别，配对研究中两个率的比较用配对χ²检验，即McNemar检验。这种研究设计的数据分析常整理为如下四格表的形式(表1)。

表1

表1中a、d为观察结果一致的两种情况，b、c为观察结果不一致的两种情况。当两种方法的总体率相等，则有总体B=总体C。但在抽样研究中抽样误差不可避免，样本中的b和c往往不等(即两样本率不等：p₁≠p₂)，所以根据样本统计量推断总体信息就要进行假设检验。这里假设检验统计量只和结果不一致的b和c有关，当b+c≥40时，用以下计算公式(1)，当20≤b+c＜40时，用以下计算公式(2)，当b+c＜20时，直接计算确切概率。

(1) \(\chi^{2}=\frac{(\mathrm{b}-\mathrm{c})^{2}}{b+c}, v=1\)

(2) \(\chi^{2}=\frac{(|\mathrm{b}-\mathrm{c}|-1)^{2}}{b+c}, v=1\)

有充分理论基础的配对卡方检验结果为什么会被质疑呢？可从下面两个案例寻找答案。

一、案例一

某实验室分别用乳胶凝集法(RPLA)和免疫荧光法(IFA)对100例患者血清中某抗体进行测定。问两种方法的检测结果有无差别？数据见表2。

表2

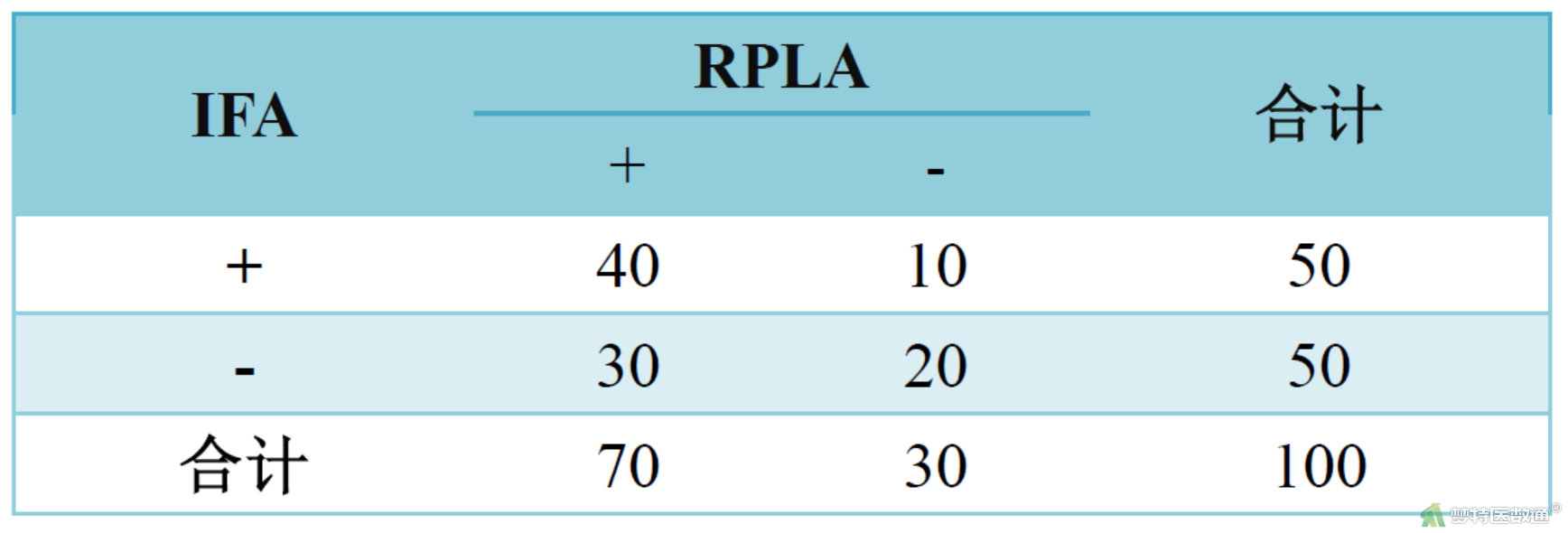
此案例中b=10，c=30，代入上述计算公式(1)，可以计算得到χ²=10，通过查询χ²界值表(链接界值表)可以得到，当υ=1时，P<0.05，提示两种方法检出的阳性率差异有统计学意义，即两种检测方法结果不同。

二、案例二

某实验室分别用乳胶凝集法(RPLA)和免疫荧光法(IFA)对1000例患者血清中某抗体进行测定。问两种方法的检测结果有无差别？数据见表3。

表3

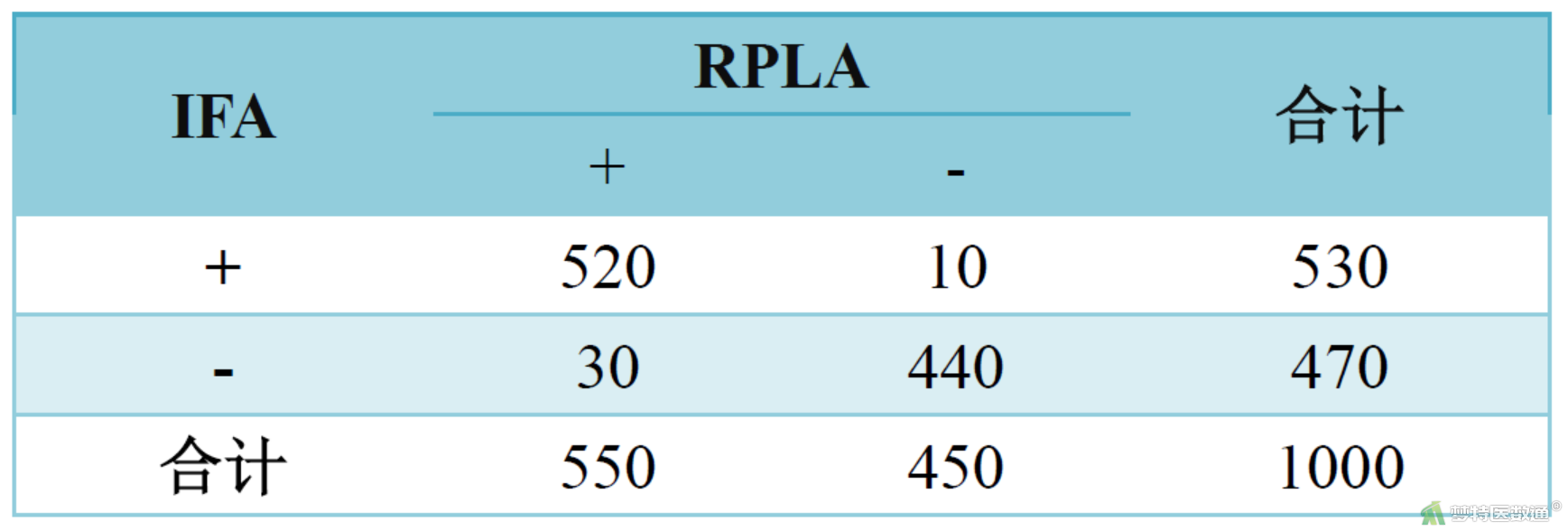
本案例中的b和c与案例一中的一样，χ²值又只与这两个数值有关，所以不用代入公式就可以知道本案例中的χ²值仍为10，P<0.05，分析结果和案例一中一样，两种方法检出的阳性率差异有统计学意义，即两种检测方法结果不同。

三、配对卡方检验结果的解读

细心的读者应该已经发现，以上两个案例检验统计量和分析结果完全一样，但案例二中的样本量是案例一中的10倍，案例二中a和d的数值也远远大于案例一中的a和d。

案例一中，两种检测方法结果不一致的比例为：

\(\frac{10+30}{100} \times 100 \%=40 \%\)

案例二中，两种检测方法结果不一致的比例仅为：

\(\frac{10+30}{1000} \times 100 \%=4 \%\)

40%显然要比4%大得多，即案例一中两种检测方法的差异确实比较大，而案例二中两种检测方法的差异其实比较小。可以推测，如果b和c的数值仍保持不变，但总样本量和表示两种方法结果一致的数值a和d都变得比案例二中更大，那么实际两种方法不一致的比例就会比4%更小。这表明两种方法的实际差异一直在缩小，但统计推断结果却一直不变，仍显示两种检测方法结果不同。那么这种情况下的配对卡方检验结果就变得不那么可信了。

通过以上案例可以发现，当样本量n很大且a与d的数值也很大(即两种方法的一致率较高)时，即使配对卡方检验结果显示有统计学意义，也不一定有实际意义。

所以，样本量大且一致率高的两种方法，配对卡方结果不那么可信，不适合通过配对卡方检验进行两种结果是否一致的统计推断。