诊断试验的正确评价是合理运用临床诊断试验的重要保障,在实际研究中常通过真实性、可靠性及临床实用性等来评价诊断试验。本文将主要介绍诊断试验的真实性评价指标及具体计算方法。
关键词:诊断试验; 真实性评价; 灵敏度; 特异度; 约登指数; 似然比; 比值比; ROC曲线下面积; 预测值
真实性(Validity)指诊断试验所取得的结果与实际(真实)情况相符合的程度,评价的指标包括灵敏度、特异度、正确率、约登指数、似然比、比值比、ROC曲线下面积及预测值。
一、案例介绍
欲评价某新方法诊断冠心病的真实性,对1000名门诊就诊者进行了新方法诊断,并使用冠状动脉造影 (金标准)进行最终诊断,假设诊断结果如表1。该新方法对冠心病诊断效果的真实性如何?
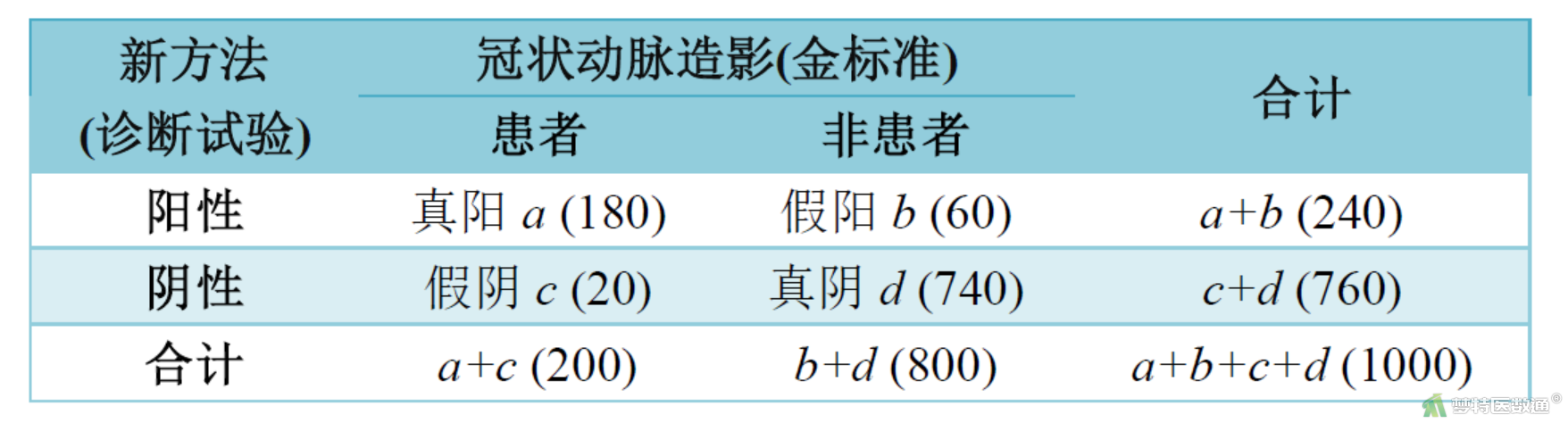
二、案例分析
临床上,冠状动脉造影可被认为诊断冠心病的金标准,欲评价某新诊断方法对冠心病诊断的真实性,可以采用灵敏度、特异度、正确率、约登指数、似然比、比值比、ROC曲线下面积及预测值等指标进行综合评价。
三、指标计算
(一) 灵敏度与漏诊率
1. 灵敏度(Sensitivity, Se)
又称真阳性率(true positive rate, TPR),是指能将实际患病的人正确诊断为患者的能力,即患者中判定为阳性结果的百分比。灵敏度越大,发现阳性(患者)的可能性越大。
计算公式及过程如下:
\(\text { 灵敏度 }(S e)=\frac{a}{a+c} \times 100 \%=\frac{180}{200} \times 100 \%=90 \%\)
表示1名冠心病患者,采用新方法检测,被正确诊断为冠心病的概率为90%。
95%置信区间(Confidence Interval, CI)计算公式及过程如下:
\(95 \% \mathrm{CI}=\mathrm{Se} \pm 1.96 \sqrt{\frac{S e(1-S e)}{a+c}}\)
即95%CI为:0.858~0.942。
2. 漏诊率
又称假阴性率(false negative rate, FNR),是指将实际患病的人错误诊断为非患者的比率。漏诊率=1-灵敏度,灵敏度越高,漏诊率越低。
计算公式及过程如下:
\(\text { 假阴性率 }(F N R)=\frac{c}{a+c} \times 100 \%=\frac{20}{200} \times 100 \%=10 \%\)
表示1名冠心病患者,采用新方法检测,被诊断为无冠心病的概率为10%。
95%CI计算公式及过程如下:
\(95 \% \mathrm{CI}=F N R \pm 1.96 \sqrt{\frac{F N R(1-F N R)}{a+c}}\)
即95%CI为:0.058~0.142。
3. 灵敏度与漏诊率的运用
当实际患病时,灵敏度大的试验更容易诊断被检查者患病的可能性。当实际不患病时,灵敏度大的试验更容易排除被检查者患病的可能性。
(二) 特异度与误诊率
1. 特异度(Specificity, Sp)
又称真阴性率(true negative rate, TNR),是指能将实际无病的人正确诊断为非患者的能力,即非患者中被判为阴性结果的百分比。特异度越大,实际无病的人被判为阴性的可能性越大。当诊断结果为阳性时,特异度大的试验更容易确诊被检查者患病的可能性。
计算公式及过程如下:
\(\text { 特异度 }(S p)=\frac{d}{b+d} \times 100 \%=\frac{740}{800} \times 100 \%=92.5 \%\)
表示1名非冠心病患者,采用新方法检测,被诊断为无冠心病的概率为92.5%。
95%CI计算公式及过程如下:
\(95 \% \mathrm{CI}=S p \pm 1.96 \sqrt{\frac{S p(1-S p)}{b+d}}\)
即95%CI为:0.907~0.943。
2. 误诊率
又称假阳性率(false positive rate, FPR),是将实际无病的人错误判断为患者的比例。误诊率=1-特异度。
计算公式及过程如下:
\(\text { 误诊率 }=\frac{b}{b+d} \times 100 \%=\frac{60}{800} \times 100 \%=7.5 \%\)
表示1名非冠心病患者,采用心电图检测,被诊断为冠心病的概率为7.5%。
95%CI计算公式及过程如下:
\(95 \% \mathrm{CI}=(1-S p) \pm 1.96 \sqrt{\frac{S p(1-S p)}{b+d}}\)
即95%CI为:0.057~0.093。
3. 特异度与误诊率的运用
当实际患病时,特异度大的试验更容易排除被检查者不患病的可能性。当实际不患病时,特异度大的试验更容易诊断被检查者不患病的可能性。
(三) 约登指数
约登指数(Youden’s index)又称正确指数,是诊断试验中灵敏度和特异度之和减去1,表示诊断试验发现真正患者和非患者的总能力。约登指数的取值介于-1~1之间,其值越大,说明诊断试验准确度越高。
计算公式及过程如下:
约登指数(γ) = 灵敏度+特异度-1 = 1-(误诊率+漏诊率) = 0.825
表示采用新方法能将门诊就诊者正确诊断是否患冠心病患者的概率为82.5%。
95%CI计算公式及过程如下:
\(95 \% \mathrm{CI}=(S e+S p-1) \pm 1.96 \sqrt{\frac{S e(1-S e)}{a+c}+\frac{S p(1-S p)}{b+d}}\)
即95%CI为:0.800~0.870。
(四) 正确率
用于真实性评价时,正确率表示诊断试验结果与金标准符合的程度,反映正确诊断患者与排除非患者的能力。计算公式如下:
\(\text { 正确率 }=\frac{a+d}{a+b+c+d} \times 100 \%=\frac{180+740}{1000} \times 100 \%=92 \%\)
表示采用新方法对门诊就诊者正确诊断的概率为92%。
95%CI计算公式及过程如下:
\(95 \% \mathrm{CI}=\text { 正确率 } \pm 1.96 \sqrt{\frac{(a+d)(b+c)}{N^{3}}}\)
即95%CI为:0.903~.937。
正确率与约登指数不同的是,前者会受患病率的影响,而后者与患病率无关(提高诊断试验效率——验前概率对正确率的影响)。
在可靠性评价中,符合率(也称紧密度、一致率、正确分类率)的计算公式与此处介绍的正确率计算公式完全一致,但意义却不一样(诊断试验评价——可靠性评价)。
(五) 似然比
似然比(likelihood ratio, LR),是指在诊断试验中患者出现某种检测结果(如阳性或阴性)的概率与非患者出现相应结果的概率之比,说明患者出现该结果的机会是非患者的多少倍,属于同时反映灵敏度和特异度的复合指标。似然比分为阳性似然比和阴性似然比。
1. 阳性似然比
阳性似然比(positive likelihood ratio, LR+)是真阳性率与假阳性率(误诊率)之比,说明正确判断阳性的可能性是错判断阳性可能性的倍数,即患者检查出阳性的可能性是非患者的多少倍,表明诊断试验结果呈阳性时患病与不患病机会的比例。
计算公式及过程如下:
\(\text { 阳性似然比 }\left(L R^{+}\right)=\frac{\text { 真阳性率 }}{\text { 假阳性率 }}=\frac{\text { 灵敏度 }}{1-\text { 特异度 }}=\frac{0.9}{0.075} = 12\)
表示采用新方法诊断结果为阳性时,患冠心病的概率是不患病概率的12倍。
2. 阴性似然比
阴性似然比(negative likelihood ratio, LR-)是假阴性率(漏诊率)与真阴性率(特异度)之比,表示错判阴性的可能性是正确判断阴性可能性的倍数,即患者检查出阴性结果的概率是非患者的多少倍,表明诊断试验结果阴性时患病与不患病的比例。
计算公式及过程如下:
\(\text { 阴性似然比 }\left(\mathrm{LR}^{-}\right)=\frac{\text { 假阴性率 }}{\text { 真阴性率 }}=\frac{1-\text { 灵敏度 }}{\text { 特异度 }}=\frac{0.1}{0.925}=0.11\)
表示采用新方法诊断结果为阴性时,患冠心病的概率是不患病概率的0.11倍。
3. 阳性似然比与阴性似然比的运用
LR+的范围为0~∞,LR+值越大,说明阳性结果与患病概率的关联越大,诊断试验的诊断价值越好。一般认为LR+≥10,表明诊断试验具有较高的诊断价值。LR-值越小,说明阴性结果与未患病概率的关联越大,诊断试验的诊断价值越好。LR-≤0.1,表明诊断试验具有较高的诊断价值。似然比与灵敏度和特异度一样,是一个相对稳定的评价指标,不受患病率的影响。在选择诊断试验时,应选择阳性似然比较高的方法。
临床诊断的目的是根据诊断试验的结果判断个体患病机会大小,灵敏度和特异度可以反映诊断试验的效果,但无法直观地反映个体患者概率的大小。似然比可以在诊断试验结果是阳性或阴性时,通过验前概率计算个体患病的验后概率大小。
计算过程如下:
\(\text { 验前比(pre-test odds) }=\frac{\text { 验前概率 }}{1-\text { 验前概率 }}\)
\(\text { 验后比(post-test odds) }=\text { 验前比 } \times \mathrm{LR}^{+}\)或\(\text { 验后比 (post-test odds) }=\text { 验前比 } \times \mathrm{LR}^{-}\)
\(\text { 验后概率 (post-test probability })=\frac{\text { 验后比 }}{\text { 验后比 }+1}\)
在筛检试验中,验前概率一般是筛检人群的患病率;在诊断试验中,验前概率一般是接收诊断的所有人中患病人数的比例(本例中为\(\frac{200}{1000} \times 100 \%=20 \%\)),此时验后概率即为阳性预测值或1-阴性预测值。
本例中验前概率为20%,通过阳性预测值可计算验后概率为75%,表示如果新方法诊断某就诊者的结果为阳性,其患冠心病的概率为75%;通过阴性预测值可计算验后概率为1-97.4%,表示如果冠脉造影诊断某就诊者的结果为阴性,其患冠心病的概率为2.6%。
(六) 诊断比值比
诊断比值比(diagnostic odds ratio, DOR)是评价诊断试验效能的综合指标,表示病例组阳性比值与对照组阳性比值的比。其值范围为0~∞,其值越大,诊断试验效能越好。DOR不受患病率的影响,并可适用于诊断试验研究的Meta分析。
计算公式及过程如下:
\(\text { 诊断比值比 }=\frac{a d}{b c}=\frac{L R^{+}}{L R^{-}}=\frac{180 \times 740}{20 \times 60}=111\)
表示使用新方法诊断冠心病患者结果有病的概率是非冠心病组中被诊断为有病概率的111倍。
95%CI计算公式及过程如下:
\(95 \% \mathrm{CI}=\exp (\ln D O R 95 \% \mathrm{CI})\)
\(=\exp (\ln D O R \pm 1.96 \sqrt{\operatorname{Var}(\ln D O R)})\)
\(=\exp \left(\ln D O R \pm 1.96 \sqrt{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}}\right)\)
即95%CI为:65.228~188.891。
(七) ROC曲线下面积
ROC曲线又称受试者工作特征 (receiver operating characteristic) 曲线,是以1-特异度为横坐标,灵敏度为纵坐标,依照连续变化的诊断阈值,由不同灵敏度和特异度刻画出的曲线。计算灵敏度和特异度时,必须将诊断试验的检测结果分为阳性和阴性两种结果。对于连续性变量或等级变量,当选择不同的诊断阈值时,计算的灵敏度和特异度可能会出现不一致的情况。ROC曲线可以全面和准确地评价诊断价值,且不受患病率的影响。
ROC曲线的价值常通过ROC曲线图形和曲线下面积(area under the ROC curve, AUC)呈现。曲线图形可以直观地描述诊断效果及灵敏度和特异度之间的变化关系。AUC值可综合评价诊断的准确性,取值范围为0~1之间,在AUC>0.5的情况下,越接近1说明诊断的准确性越高;在AUC<0.5的情况下,越接近0说明诊断的准确性越高。一般AUC>0.5情形更为多见,其常见判断标准如表2所示。

本例中的AUC值经过SPSS软件计算,AUC=0.913,95%CI:0.886~0.939,表明心电图对冠心病的诊断价值较高。ROC曲线如图1所示。
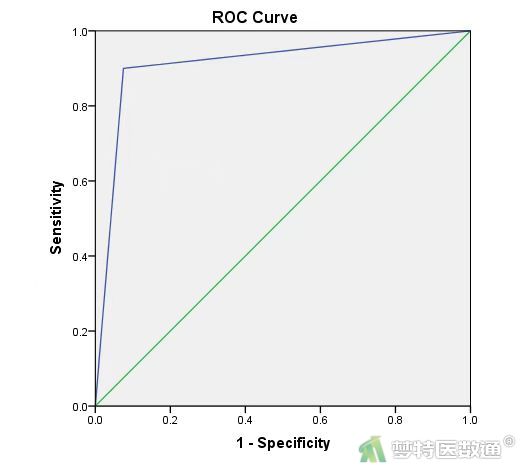
(八) 预测值
预测值又称诊断价值,是指在已知试验结果(阳性或阴性)的条件下,表明有无疾病的概率,其中包括阳性预测值和阴性预测值。
1. 阳性预测值
阳性预测值(positive predictive value, PV+)是试验阳性结果中真正有疾病的概率。
计算公式及过程如下:
\(\text { 阳性预测值 }\left(P V^{+}\right)=\frac{a}{a+b} \times 100 \%=\frac{180}{180+60} \times 100 \%=75 \%\)
表示采用新方法诊断为患病的就诊者中真正患冠心病的概率为75%。
95%CI计算公式及过程如下:
\(95 \% \mathrm{CI}=\frac{a}{a+b} \pm 1.96 \sqrt{\frac{a b}{(a+b)^{3}}}\)
即95%CI为:0.695~0.805。
2. 阴性预测值
阴性预测值(negative predictive value, PV-)是诊断试验阴性结果中真正无病的概率。
计算公式及过程如下:
\(\text { 阴性预测值 }\left(P V^{-}\right)=\frac{d}{c+d} \times 100 \%=\frac{740}{20+740} \times 100 \%=97.4 \%\)
表示采用新方法诊断为非患者的就诊者中真正不患冠心病的概率为97.4%。
95%CI计算公式及过程如下:
\(95 \% \mathrm{CI}=\frac{d}{c+d} \pm 1.96 \sqrt{\frac{c d}{(c+d)^{3}}}\)
即95%CI为:0.962~0.985。
3. 预测值的运用
在患病率不变的情况下,诊断试验的灵敏度越高,阴性预测值越好,有足够的把握判断阴性结果为非患者;反之,特异度越高,阳性预测值越好,有足够个把握判断阳性结果为患者。
当诊断试验的灵敏度和特异度一定时,就诊者的患病率越低,阳性预测值越差(提高诊断试验效率——为什么要考虑患病率(验前概率)?提高诊断试验效率——验前概率对验后概率的影响。)。因此,临床医生在判断试验结果时应综合考虑试验的灵敏度、特异度以及就诊人群的患病率来提高诊断试验结果的把握度。