前面介绍了医学研究之诊断试验——真实性评价,本文主要介绍诊断试验的可靠性评价指标及具体计算方法。
关键词:诊断试验; 可靠性评价; 符合率; Kappa值; 组内相关系数; ICC系数
真实性(validity)是指诊断试验所取得的结果与实际(真实)情况相符合的程度,也称准确性或效度;评价的指标包括灵敏度、特异度、约登指数、似然比、比值比、ROC曲线下面积及预测值。可靠性(reliability)是指在相同条件下同一诊断试验对相同人群重复试验,或不同诊断试验(评价人员)对同一人群进行试验,获得相同结果的稳定程度,也称为信度。可靠性越高,说明试验结果受随机误差的影响越小,评价的指标包括符合率、Kappa值、组内相关系数和变异系数。
一、符合率(agreement/consistency)
符合率又称精密度(precision)、一致率(consistency rate)或正确分类率(correct classification rate),是指一项诊断试验重复测量相同研究对象,或不同诊断试验(评价人员)对同一人群进行试验,结果一致的阳性数与阴性数之和占所有参加诊断试验人数的比例。符合率可以通过利用判断结果不一致(表1中b和c)信息反映诊断试验的可靠性,包括粗一致率和调整一致率。
表1 两种方法对冠心病的诊断结果
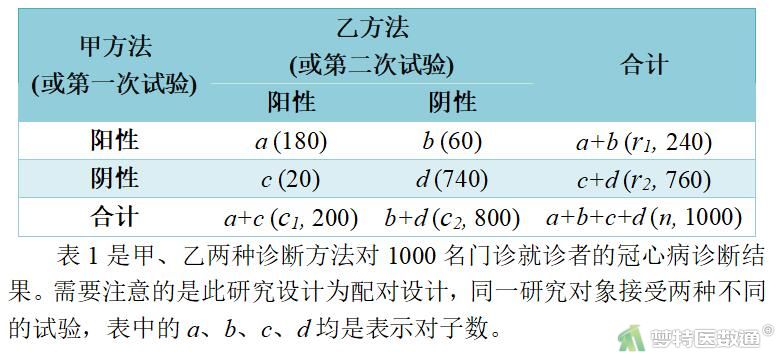
表1是甲、乙两种诊断方法对1000名门诊就诊者的冠心病诊断结果。需要注意的是此研究设计为配对设计,同一研究对象接受两种不同的试验,表中的a、b、c、d均是表示对子数。
(一) 粗一致率(crude agreement)
计算公式及过程如下:
\(\text { 粗一致率 }=\frac{a+d}{a+b+c+d} \times 100 \%=\frac{920}{1000} \times 100 \%=92 \%\)
表示甲、乙两种方法诊断结果的一致性为92%。
95%置信区间(confidence interval, CI)计算公式及过程如下:
\(95 \% C I=\text { 粗一致率 } \pm 1.96 \sqrt{\frac{(a+d)(b+c)}{N^{3}}}\)
可计算95%CI为:0.903~0.937。
(二) 调整一致率(adjusted agreement)
计算公式及过程如下:
\(\text { 调整一致率 }=\frac{1}{4} \times\left(\frac{a}{a+b}+\frac{a}{a+c}+\frac{d}{c+d}+\frac{d}{b+d}\right) \times 100 \%=\frac{26970}{30400} \times 100 \%=88.72 \% \text {. }\)
调整一致率的意义与粗一致率一样,只是进行校正从而减少误差。
二、Kappa值
临床上需要用一致性分析来评价不同方法(或不同评价者)对同一人群的诊断(评价)结果是否存在差异,通常可采用Kappa值分析。Kappa值是一个有效地测量分类变量可靠性的指标,该值考虑了机遇因素对一致性的影响,其取值范围为-1~1,若K为负数,说明观察一致率比机遇造成的一致率还小;K=0,表示观察一致率完全由机遇所致;K>0,表示观察的一致率大于机遇一致率;K=1,表明两者的判断结果完全一致。Kappa值可分为Cohen's Kappa值和加权Kappa值,前者常用于二分类、无序多分类评价结果;后者用于有序多分类评价结果。
(一) Cohen's Kappa值
Cohen's Kappa值即简单Kappa值,通过实际一致性与机遇一致性的比值计算所得,常用的判断说明如下:
表2 Cohen's Kappa值判断说明

此处仍以表1案例计算相关指标。
1. 二分类资料的Cohen's Kappa值
(1) 计算观察一致率(observed agreement, P0)
\(P_{0}=\frac{a+d}{n} \times 100 \%=\frac{180+740}{1000} \times 100 \%=92 \%\)
(2) 计算机遇一致率(chance agreement, Pc)
\(P_{\mathrm{c}}=\frac{\frac{r_{1} c_{1}}{n}+\frac{r_{2} c_{2}}{n}}{n}=\frac{\frac{240 \times 200}{1000}+\frac{760 \times 800}{1000}}{1000}=0.656\)
(3) 计算非机遇一致率(potential agreement beyond chance)
\(\text { 非机遇一致率=1-机遇一致率 }=1-P_{c}=1-0.656=0.344\)
(4) 计算实际一致率(actual agreement beyond chance)
\(\text { 实际一致率=观察一致率-机遇一致率 }=P_{0}-P_{c}=0.92-0.656=0.264\)
(5) 计算Kappa值(K)
\(K=\frac{\text { 实际一致率 }}{\text { 非机遇一致率 }}=\frac{P_{0}-P_{C}}{1-P_{C}}=\frac{0.264}{0.344} \times 100 \%=76.7 \%\)
可知甲、乙两种方法对冠心病诊断的一致性极好。
(6) 计算95%CI
\(95 \% C I=K \pm 1.96 \sqrt{\frac{\left(p_{0}\right)\left(1-p_{0}\right)}{N\left(1-p_{0}\right)^{2}}}\)
可计算95%CI为:0.557~0.977。
(7) 假设检验
\(u=\frac{k}{s_{k}}=\frac{k}{\sqrt{\frac{\left(p_{0}\right)\left(1-p_{0}\right)}{N\left(1-p_{0}\right)}}}=\frac{0.767}{0.107}=7.156\)
查u界值表,可知u=7.156>2.58,故P<0.01,认为K值因机遇所致的可能性较小,即K值有统计学意义。
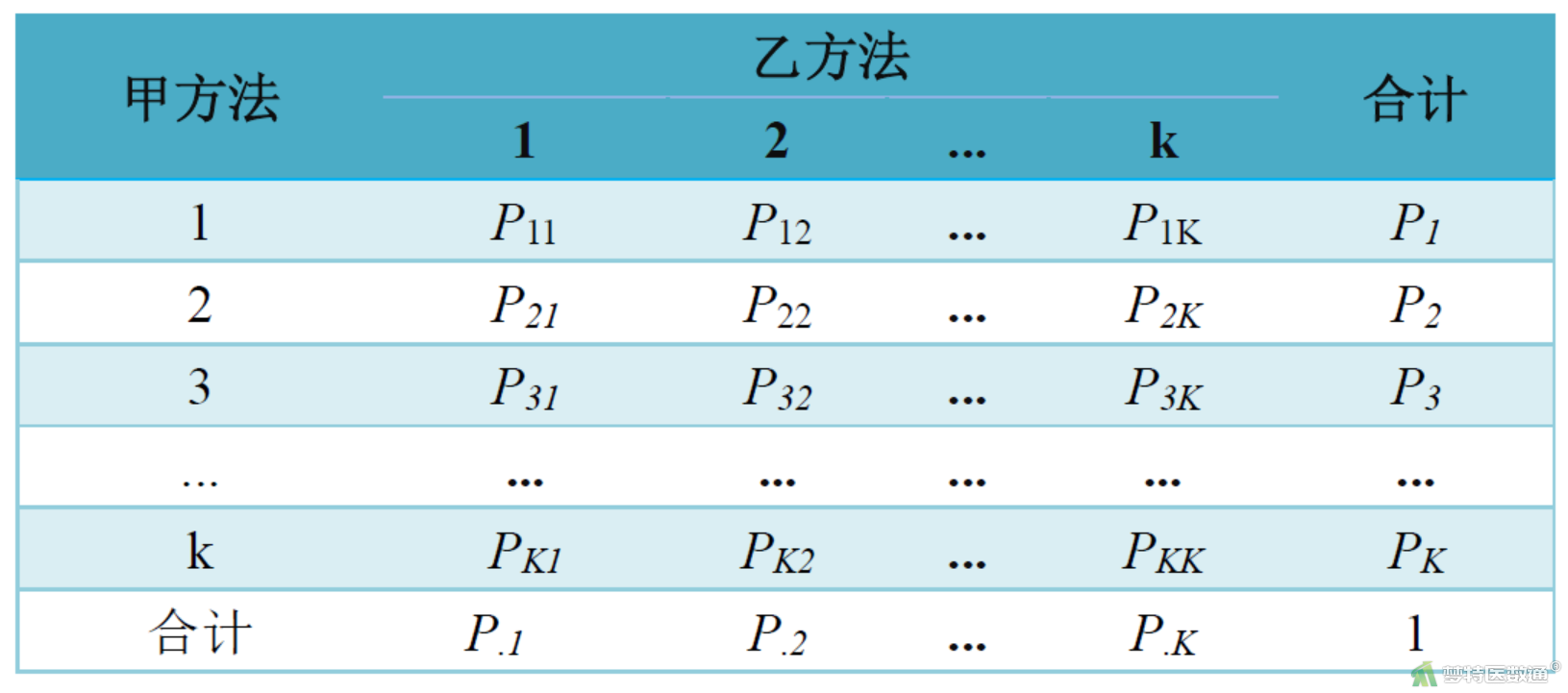
2. 无序多分类资料的Cohen's Kappa值
对于多分类资料资料(如表3)不宜用四格表的Kappa分析方法,而应用K×K表的Kappa分析,表3中各格子的数据Pij为构成比,计算方法是将每个格子的实际频数除以总频数。
表3 Kappa分析的K×K表
计算公式及过程:
(1) 计算观察一致率:
\(\left(P_{0}\right)=\sum_{i=1}^{\mathrm{k}} p_{i i}\)
(2) 计算机遇一致率:
\(\left(P_{C}\right)=\sum_{i=1}^{\mathrm{k}} p_{i .} p_{. i}\)
(3) 计算Kappa值(K):
\(K=\frac{P_{0}-P_{c}}{1-P_{c}}\)
(4) 计算标准误:
\(S E(k)=\frac{\sqrt{P_{e}+P_{e}^{2}-\sum_{i=1}^{k} P_{i .} P_{. i}\left(P_{i .}+P_{. i}\right)}}{\left(1-P_{e}\right) \sqrt{n}}\)
(5) 计算95CI%:
\(K \pm 1.96 \times S E(K)\)
(6) 案例介绍及计算:
两名放射科医生对55名就诊者进行肝癌诊断。判断结果为:1=“不确定”,2=“良性”,'3=“恶性”,其判断结果如表4。
表4 A、B两名医生对肝癌的诊断结果
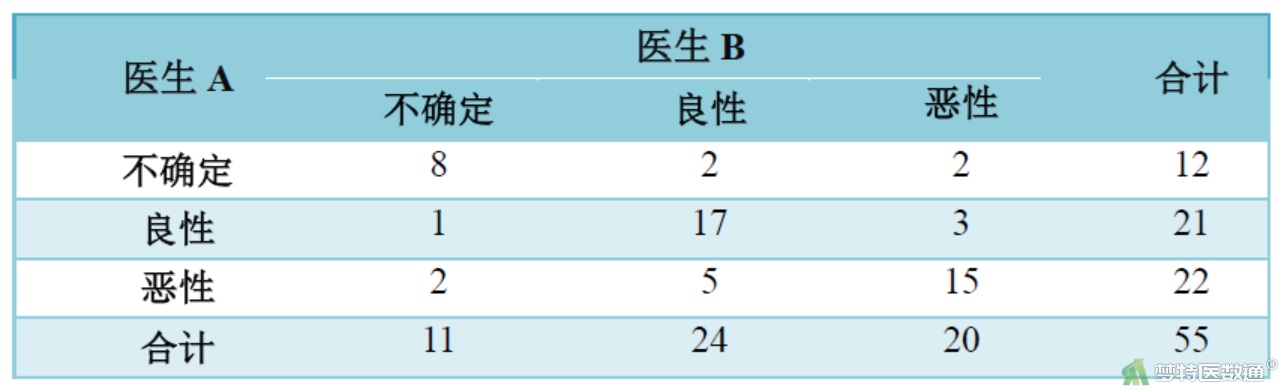
因采用公式计算相对繁琐,本案例直接采用SPSS软件计算得到:
Kappa值=0.577 (P<0.001),95%CI: 0.395~0.759
提示两名医师诊断结果具有一致性,参考Kappa值的判断标准,可知医生A与医生B诊断结果的一致性为中等。
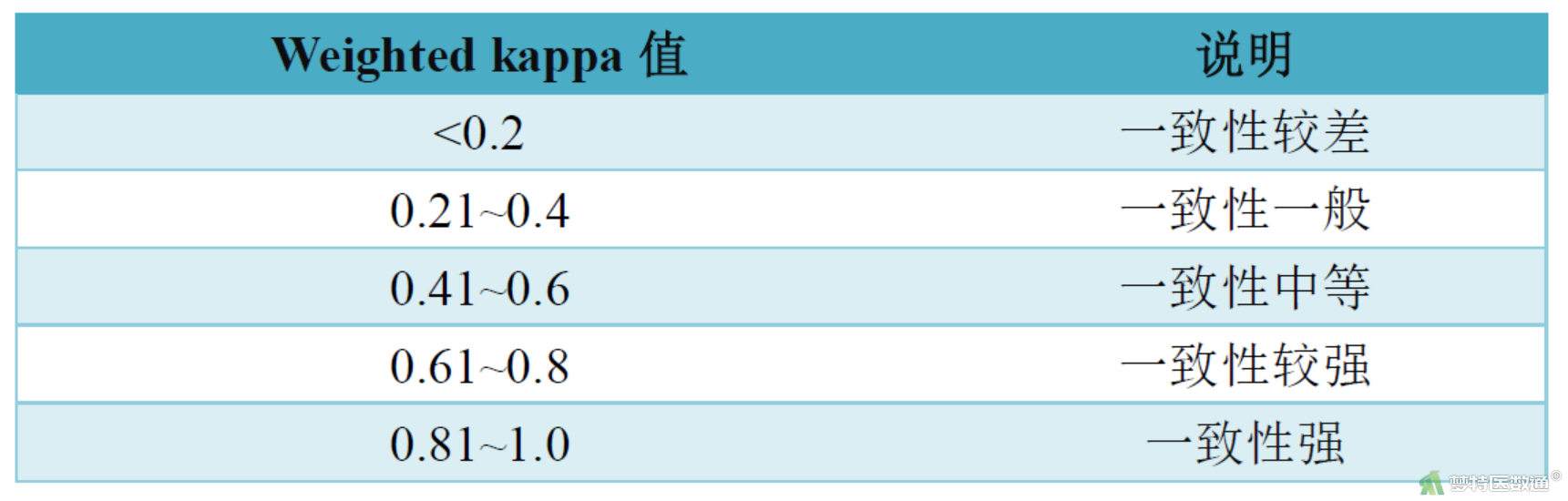
(二) 加权Kappa值
加权Kappa值可用于有序多分类诊断结果的一致性评价。加权Kappa系数是Cohen's Kappa系数的推广,是用加权的方法对两个评价结果进行量化所得。加权Kappa系数取值范围为-1~1。其常用的判断说明如表5。
表5 Weighted Kappa值判断说明
三、组内相关系数(intra-class correlation coefficient, ICC)
(一) ICC介绍
ICC是两种诊断方法测量结果的变异占总变异的比例,同时考虑了系统误差与随机误差的影响。ICC不仅适用于计量资料,也适用于有序分类变量的一致性评价。
计算公式为:
\(I C C=\frac{M S_{\text {区组}}-M S_{\text {误差}}}{M S_{\text {区组}}+(k-1) M S_{\text {误差}}+\frac{k\left(M S_{\text {处理}}-M S_{\text {误差}}\right)}{n}}\)
其中,MS区组为随机区组(被观察对象)间的均方(方差),MS误差为误差的均方,MS处理为处理组(检测方法)的均方。k为重复次数(测量方法的数量),n为被观察对象的例数。ICC介于0~1之间,0表示完全不一致,1表示完全一致。其推荐的判断说明如下:
表6 组内相关系数(ICC)判断说明
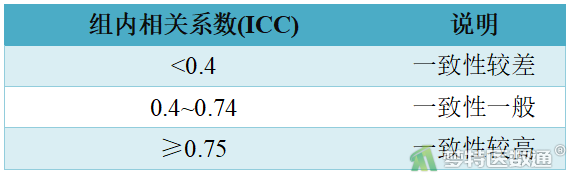
ICC评价一致性可以同时兼顾系统误差和随机误差,与配对t检验和Pearson相关分析相比,具有其独特的优势。但当样本量较小时,ICC系数容易被低估。
(二) 案例介绍
使用甲、乙种方法测量18名就诊者的某生化指标,检测结果如表7所示,请对这两种方法的可靠性进行评价。
表7 甲、乙两种方法检测某生化指标的结果
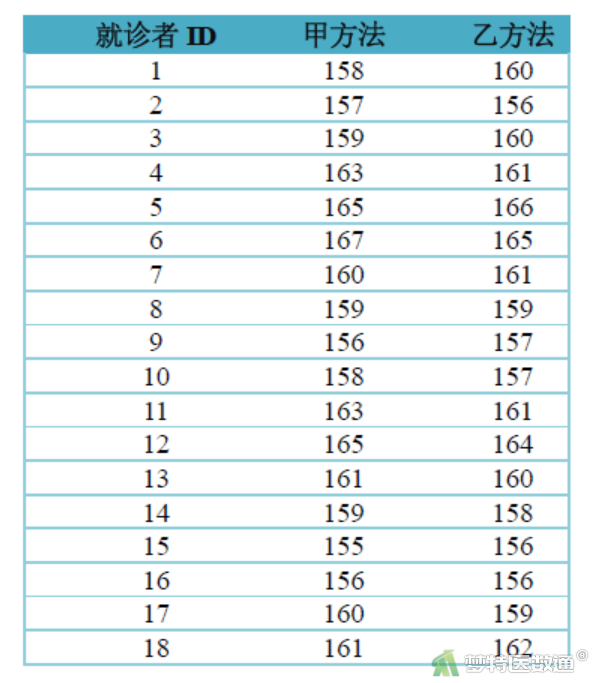
该案例中的指标为连续性变量,可以采用ICC进行可靠性评价。使用SPSS软件计算得到:
ICC=0.925,95%CI:0.813~0.971,P<0.001
表示两者检测结果一致性较高。
四、变异系数(coefficient of variation,CV)
(一) CV介绍
CV是标准差与平均数的比值,它可以消除单位和(或)平均数不同对两个或多个资料变异程度比较的影响。
计算公式为:
\(C V=\frac{\text { 标准差 }(S D)}{\text { 平均值 }(M)}\)
(二) 案例介绍
某实验室采用新批次试剂进行20次测量,其测量结果的标准差(s)为0.43,均数(\(\overline{\mathcal{X}}\))为2.78。已知该实验室此前建立的参考CV值(CV参考)为16.4%,请对新批次试剂测量的的可靠性进行评价。
\(C V=\frac{\text { 标准差 }(S D)}{\text { 平均值 }(M)}=\frac{0.43}{2.78} \times 100 \%=15.5 \%\)
实验室中常通过考察CV值是否在CV参考×(1±10%)内评价检测结果的可靠性,如果超出这个范围,就要对实验结果进行原因分析。已知CV参考×(1±10%)为14.8%~18.0%,该例中CV值=15.5%,在14.8%~18.0%范围内,提示新批次试剂的可靠性较好,测量的数据可用于建立下次实验室的CV参考。
五、影响诊断试验可靠性的因素
一项诊断试验的可靠性受很多因素的影响,包括试验方法本身及其外界条件、观察者及被观察者三方面的变异。
(一) 试验方法与条件的差异
包括试验的环境条件,如温度、湿度等;试剂与药品的质量及配置方法;仪器是否校准以及操作者的熟练程度等。因此,在诊断试验中,应严格规定试验环境条件以及统一试剂与药品的批次,仪器需要提前校准,这样才能保证试验的可靠性。
(二) 观察者的变异
包括不同观察者间变异和同一观察者不同次数间的变异,即在不同时间、条件下重复检查同一样本时所得结果的不一致性。如,不同医生使用同一个血压计对同一个人血压值的测量,结果可能不完全相同;同一个医生在不同环境和条件下使用同一个血压计对同一个人血压值的测量结果也不完全一样。因此,观察者需要严格培训,统一判断标准,使观察者的变异降低到允许范围内。
(三) 被观察者的变异
主要是指个体的生物学变异,即被观察者个体的各种生理、生化测量值均随测量时间、条件等变化而不断变化。例如,血糖值在餐前、餐后,上午、下午不同时间均不同,在可靠性评价过程中需要排除个体生物学变异的干扰。因此,在诊断试验中要严格统一测量时间和测量条件,使被观察者在相同条件下进行比较。