提高诊断试验效率——验前概率对验后概率的影响

关键词：诊断试验; 患病率; 验前概率; 阳性预测值; 阴性预测值; 验后概率

一、验后概率

诊断检查阳性结果并不意味着肯定患病，阴性结果也并不意味着肯定没患病。当诊断检查结果为阳性或者阴性时，就诊者患病或不患病的几率究竟有多大？在提高诊断试验效率——为什么要考虑患病率？一文中，已经举例说明了灵敏度和特异度并不能完全回答这个问题，因为相同的诊断检查用于患病率(验前概率)很低的人群时，即使灵敏度很高，阳性预测值也不一定很高，在阳性结果中可能存在很多假阳性，此时认为就诊者患病的把握并不高。反之同理，相同的诊断检查用于患病率(验前概率)很高的人群时，即使特异度很高，阴性预测值也不一定很高，在阴性结果中可能存在很多假阴性，此时认为就诊者没患病的把握并不高。因此，临床诊断时，并非完全依据诊断检查的结果，而是综合考虑就诊者的验前概率综合作出结论，此时验后概率便提供了参考价值。

验后概率(post-test probability)是指在进行完某一诊断检查后，根据就诊者罹患该疾病的验前概率和该诊断检查的相关参数(如似然比、灵敏度、特异度等)计算就诊者患病的概率，以便更确切地对就诊者做出诊断。验后概率因为代表了诊断检查之后的患病概率，因此也称为修正或事后患病概率。根据似然比和验前概率，可计算验后概率。

如果诊断结果为阳性，验后概率的计算公式如下：

（1）验前比(pre-test odds) =\(\frac{\text { 验前概率}}{1-\text { 验前概率 }}\)

（2）验后比(post-test odds) = 验前比×阳性似然比(LR⁺)

（3）验后概率(post-test probability) =\(\frac{\text { 验后比 }}{\text { 验后比 }+1}\)

如果诊断结果为阴性，验后概率的计算公式如下：

（4）验前比(pre-test odds) =\(\frac{\text { 验前概率}}{1-\text { 验前概率 }}\)

（5）验后比(post-test odds) = 验前比×阴性似然比(LR^-)

（6）验后概率(post-test probability) =\(\frac{\text { 验后比 }}{\text { 验后比 }+1}\)

二、验后概率与预测值的关系

(一) 预测值

又称诊断价值，是指在已知诊断试验结果(阳性或阴性)的条件下，患病(或无病)的概率。其中阳性预测值(positive predictive value, PV⁺)是指阳性结果中真正患病的概率。阴性预测值(nagtive predictive value, PV^-)是指阴性结果中真正未患病的概率。

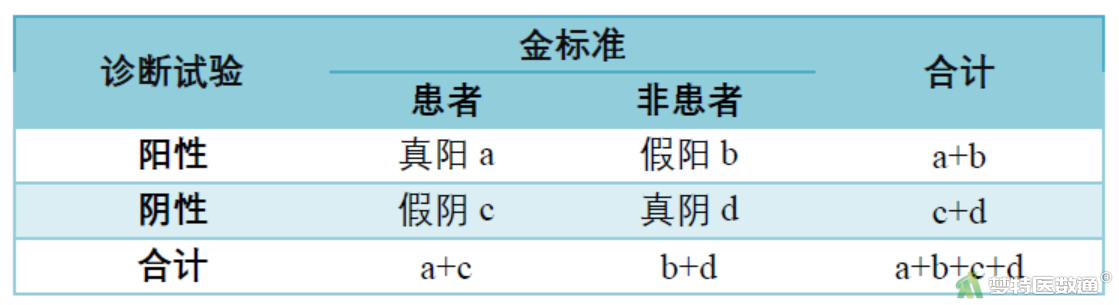
（7）阳性预测值(PV⁺) = \(\frac{a}{a+b} \times 100 \%\)

（8）阴性预测值(PV^-)= \(\frac{\mathrm{d}}{\mathrm{c}+\mathrm{d}} \times 100 \%\)

(二) 验后概率与预测值的关系

当检测结果是阳性时，阳性预测值即为验后概率；当检测结果是阴性时，1-阴性预测值即为验后概率。证明过程如下：

假如已知某人群的患病率(p)、诊断试验的灵敏度(Se)和特异度(Sp)，则诊断试验的结果可表述为图2。

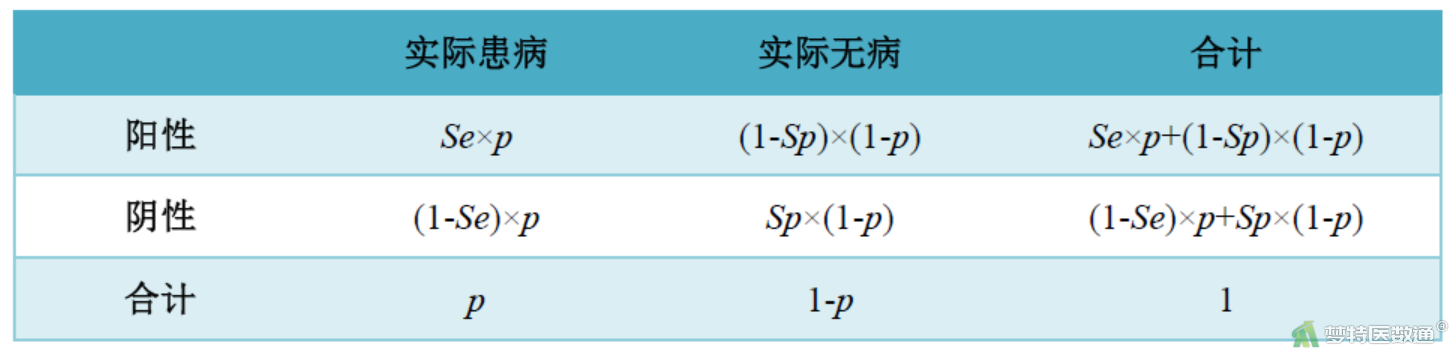
根据公式(7)、(8)和图2可知，患病率、灵敏度、特异度与预测值的关系表达式为：

（9）阳性预测值(PV⁺) =\(\frac{S e \times p}{S e \times p+(1-S p) \times(1-p)}\)

（10）阴性预测值(PV^-) =\(\frac{S p \times(1-p)}{(1-S e) \times p+S p \times(1-p)}\)

当检测结果是阳性时，根据似然比计算验后概率： 

验前比 =\(\frac{\text { 验前概率}}{1-\text { 验前概率 }}\)=\(\frac{p}{1-p}\)

验后比 = 验前比×阳性似然比(LR⁺) =\(\frac{p}{1-p} \times \frac{\mathrm{Se}}{1-\mathrm{S} p}\)

（11）验后概率 =\(\frac{\text { 验后比 }}{\text { 验后比 }+1}\)=\(\frac{\frac{p}{1-p} \times \frac{S e}{1-S p}}{1+\frac{p}{1-p} \times \frac{S e}{1-S p}}\)=\(\frac{\frac{S e \times p}{(1-S p) \times(1-p)}}{\frac{(1-S p) \times(1-p)+S e \times p}{(1-S p) \times(1-p)}}\)=\(\frac{S e \times p}{(1-S p) \times(1-p)+S e \times p}\)

当检测结果是阴性时，根据似然比计算验后概率：

验前比 =\(\frac{\text { 验前概率}}{1-\text { 验前概率 }}\)=\(\frac{p}{1-p}\)

验后比 = 验前比×阴性似然比(LR^-) =\(\frac{p}{1-p} \times \frac{1-S e}{\mathrm{~S} p}\)

（12）验后概率 =\(\frac{\text { 验后比 }}{\text { 验后比 }+1}\)=\(\frac{\frac{p}{1-p} \times \frac{1-S e}{S p}}{1+\frac{p}{1-p} \times \frac{1-S e}{S p}}\)=\(\frac{\frac{\left(1-S_{e}\right) \times p}{S p(1-p)}}{\frac{S p(1-p)+(1-S e) \times p}{S p(1-p)}}\)=\(\frac{(1-S e) \times p}{S p(1-p)+(1-S e) \times p}\)

（13）1-阴性预测值 =\(1-\frac{S p \times(1-p)}{(1-S e) \times p+S p \times(1-p)}\)=\(\frac{(1-S e) \times p+S p \times(1-p)-S p \times(1-p)}{(1-S e) \times p+S p \times(1-p)}\)=\(\frac{(1-S e) \times p}{S p(1-p)+(1-S e) \times p}\)

由以上公式可知，公式(9)与公式(11)等价，公式(12)与公式(13)等价，所以检测结果是阳性时，阳性预测值即为验后概率；检测结果是阴性时，1-阴性预测值即为验后概率。

 三、验前概率(患病率)与验后概率(预测值)的关系

由验后概率(预测值)的计算过程可知，预测值受到诊断试验的灵敏度、特异度和患病率的影响。一般来说某种诊断试验针对某种疾病的灵敏度、特异度相对固定，此时，验后概率主要与验前概率(患病率)的高低有关。假设某诊断试验的灵敏度和特异度均为90%，其验后概率(阳性预测值、1-阴性预测值)与验前概率的关系如图3、图4和图5所示。

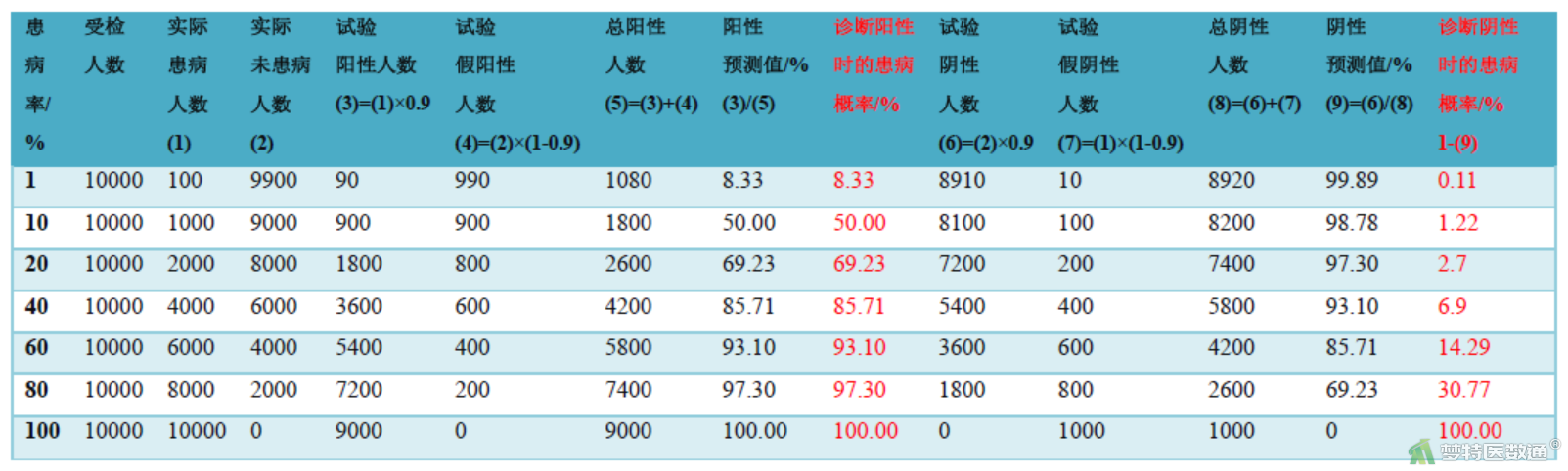
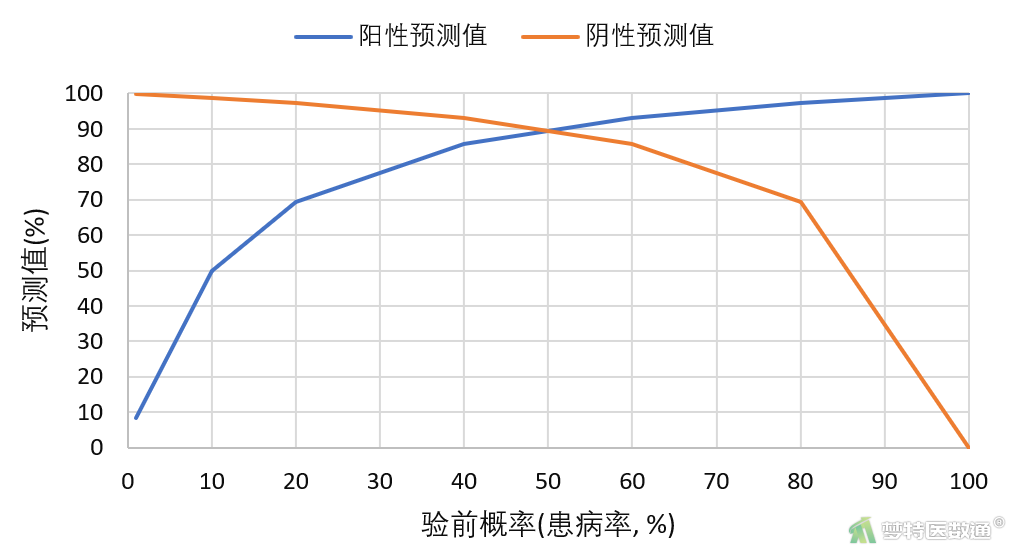
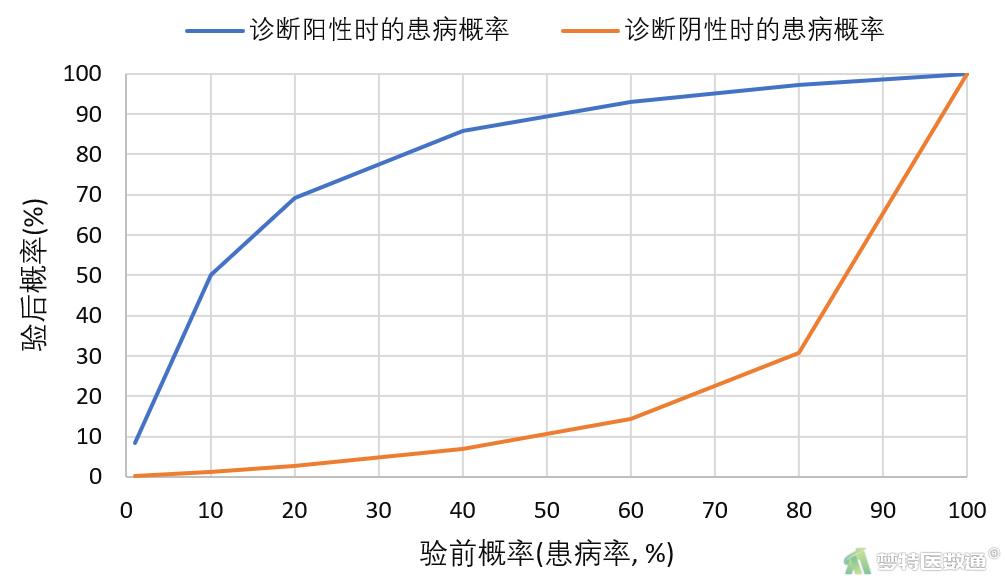
由图4可知，随着患病率的增加，阳性预测值增加，而阴性预测值降低；即随着患病率增加，诊断患者患病的把握越来越大，而诊断非患者不患病的把握越来越低。且在患病率较低时，阳性预测值的上升速度大于阴性预测值的下降速度，说明在诊断人群患病率较低时，患病率对阳性预测值的影响更明显。在患病率较高时，阴性预测值的下降速度大于阳性预测值的上升速度，说明在诊断人群患病率较高时，患病率对阴性预测值的影响更明显。

由图5可知，无论诊断试验结果是阳性还是阴性，随着患病率的增加，患者真正患病的几率均呈上升趋势。其更加重要的临床意义在于，当诊断试验用于患病率很高的人群时，就算诊断试验结果是阴性，其真正患病的概率(验后概率)也是很高的，此时不能轻易认为就诊者未患病，最好再使用特异度更高的方法再次进行检测；当诊断试验用于患病率很低的人群时，就算诊断试验结果是阳性，其真正患病的概率也是很低的，此时不能轻易认为就诊者就是患病，最好再使用灵敏度更高的方法再次进行检测。

四、应用举例

(一) 案例一

王某，28岁，体重正常、血压血脂正常，无冠心病家族史，假设取普通人群的冠心病患病率1.23%为验前概率；使用心电图(假设灵敏度为90%、特异度为90%)检查王某，试分析患冠心病的概率。

当心电图检查结果是阳性时，患病的概率为：

验后概率 =\(\frac{S e \times p}{S e \times p+(1-S p) \times(1-p)} \times 100 \%\)

=\(\frac{0.9 \times 0.0123}{0.9 \times 0.0123+(1-0.9) \times(1-0.0123)} \times 100 \%\)= 10.0783%

当心电图检查结果是阴性时，患病的概率为：

验后概率 = 1-阴性预测值=\(1-\frac{S p \times(1-p)}{(1-S e) \times p+S p \times(1-p)} \times 100 \%\)

=\(1-\frac{0.9 \times(1-0.0123)}{(1-0.9) \times 0.0123+0.9 \times(1-0.0123)} \times 100 \%\)= 0.13818%

可知，如果检测结果为阳性，则王某患冠心病的概率从1.23%提升至10.0783%，患病的把握度得到了提高；如果检测结果为阴性，则王某患冠心病的概率从1.23%下降至0.13818%，不患病的把握度得到了提高。说明通过诊断试验充分利用验前概率、灵敏度、特异度可进一步提升疾病诊断的把握度。只不过由于本案例中普通人群的冠心病患病率较低，就算心电图诊断结果是阳性，认为患病的把握度仍然不高，若要认为王某患冠心病需要慎重。

(二) 案例二

张某，65岁，肥胖、血压血脂异常，有冠心病家族史，假设根据其具有的危险因素预估患冠心病的验前概率为30%；使用心电图(假设灵敏度为90%、特异度为90%)检查张某，试分析患冠心病的概率。

当心电图检查结果是阳性时，患病的概率为：

验后概率 =\(\frac{S e \times p}{S e \times p+(1-S p) \times(1-p)} \times 100 \%\)

=\(\frac{0.9 \times 0.3}{0.9 \times 0.3+(1-0.9) \times(1-0.3)} \times 100 \%\)= 79.41176%

当心电图检查结果是阴性时，患病的概率为：

验后概率 = 1-阴性预测值=\(1-\frac{S p \times(1-p)}{(1-S e) \times p+S p \times(1-p)} \times 100 \%\)

=\(1-\frac{0.9 \times(1-0.3)}{(1-0.9) \times 0.3+0.9 \times(1-0.3)} \times 100 \%\)= 4.54545%

可知，如果检测结果为阳性，则王某患冠心病的概率从30%提升至79.41176%，患病的把握度得到了提高；如果检测结果为阴性，则王某患冠心病的概率从30%下降至4.54545%，不患病的把握度得到了提高。与案例一相比，由于验前概率提高，疾病诊断的把握度得到了显著提升。

五、验后概率计算的常用方法

(一) 计算法一

如果已知验前概率，诊断试验的灵敏度、特异度，当诊断试验结果是阳性时，可通过公式(11)计算验后概率；当诊断试验结果是阴性时，可通过公式(13)计算验后概率。

(二) 计算法二

如果已知验前概率，诊断试验的阳性预测值和阴性预测值，当诊断试验结果是阳性时，可通过公式(1)(2)(3)计算验后概率；当诊断试验结果是阴性时，可通过公式(4)(5)(6)计算验后概率。

(三) 图示法

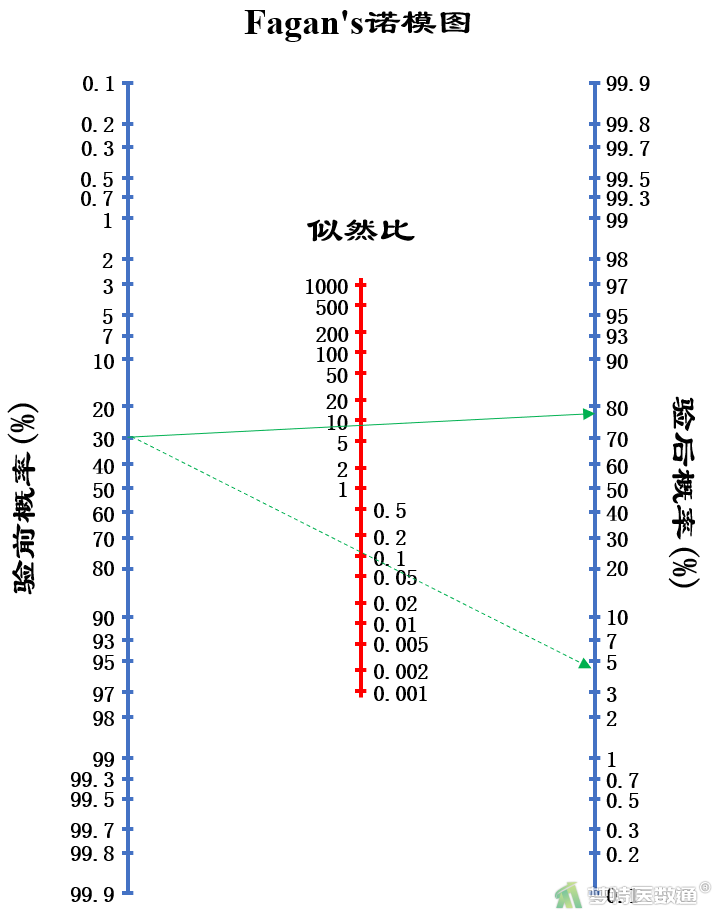
如果已知验前概率，诊断试验的阳性预测值和阴性预测值，还可通过Fagan's诺模图近似计算验后概率。在图中，左栏代表验前概率, 中间栏代表似然比, 右栏代表验后概率, 将验前概率和似然比对应的数值连线并延长，即可得到验后概率。如案例二中，通过诺模图(图6)可计算诊断阳性结果的验后概率约为97%，诊断阴性结果的验后概率约为4.5%，非常接近公式法计算结果。原版诺模图可从“附件下载”处下载。

六、小结

一个诊断试验对诊断某种疾病的灵敏度和特异性已经固定，验后概率(预测值)主要受患病率的影响。所以在开展某项诊断研究，评价该诊断试验的效果时需要考虑受检人群的患病率。可先根据就诊者的病史、体征等临床资料或其他方法估计受试者的患病率(验前概率)，再结合某项特定的诊断试验结果，估计就诊者的验后患病率(验后概率)，以提高对疾病诊断的准确性。