单样本t检验(One Sample t-test)——Python软件实现

关键词：Python; t检验; 单样本t检验; 适用条件

一、案例介绍

某医生测量了52名特殊作业成年男性工人的血红蛋白含量，即判断研究对象的血红蛋白含量均值与正常成年男性血红蛋白含量均值之间是否有差异。假设已知正常成年男性血红蛋白含量均数为145g/L，试问特殊作业成年男性工人的血红蛋白含量是否与正常成年男性有差异？

二、问题分析

本案例的分析目的是比较研究样本与已知均数是否相同。针对这种情况可以使用单样本t检验。但需要满足4个条件：

条件1：观察变量为连续变量。本研究中的血红蛋白为连续变量，该条件满足。

条件2：观测值相互独立。本研究中各研究对象的观测值都是独立的，不存在互相干扰的情况，该条件满足。

条件3：观察变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件4：观察变量为正态或近似正态分布，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

import pandas as pd  
import numpy as np  
df = pd.read_csv(r'D:单样本t检验.csv',index_col=0)  #读取文件
df2 = df.rename(columns={'Hb':'血红蛋白'}) #对变量Hb进行重命名
df.info()   #查看数据结构-图1
df2#显示df2-图2

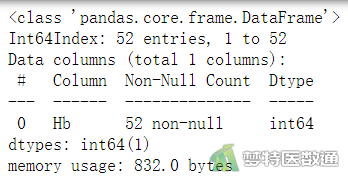
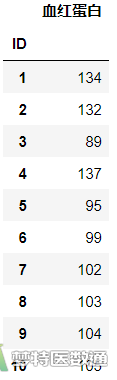
查看数据框结构并显示数据情况可见，数据共有1个变量和52个观察数据，变量代表被调查者对应的血红蛋白含量(Hb)。

(二) 适用条件判断

1. 条件3判断 (异常值判断)

(1) 软件操作

#查看最大值和最小值#

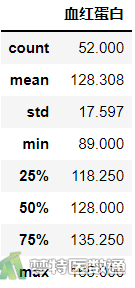
round(df2.describe(),3)  #计算基本统计量并保留3位小数

#绘制箱线图#

import matplotlib.pyplot as plt
plt.boxplot(df2)
plt.show()

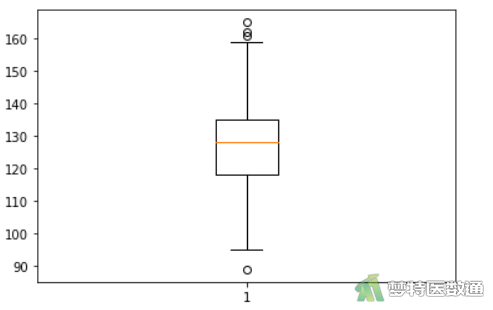
(2) 结果解读

图3列出了观察变量的“Min (最小值)”“1st Qu (P25)”“Median (中位数)”“Mean (平均值)”“3rd Qu (P75)”和“Max (最大值)”，依据专业可判断人体血红蛋白含量均可能存在89g/L和165g/L的情况；图4中箱线图提示的异常值为数据的最大值和最小值。综上，本案例未发现需要处理的异常值，满足条件3。

2. 条件4判断 (正态性检验)

(1) 软件操作

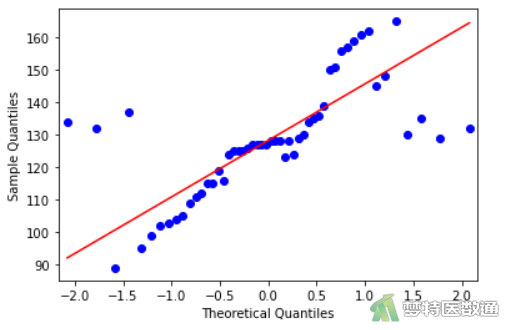
#绘制Q-Q图#

import statsmodels.api as sm
import pylab
sm.qqplot(df2, line='s')
pylab.show()

#进行Shapiro正态性检验#

from scipy import stats
shapiro_test = stats.shapiro(df2)
print(shapiro_test)

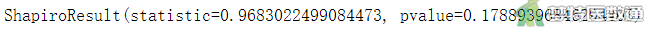
(2) 结果解读

Q-Q图上散点基本围绕对角线分布，提示数据呈正态分布；图6的“Shapiro-Wilk normality test (夏皮罗-威尔克正态性检验)”表格结果显示P≈0.1789>0.1，也提示数据服从正态分布。综上，本案例满足条件4。关于正态性检验的更多内容请阅读(医学统计学核心概念及重要假设检验的软件实现(2/4) ——正态性假设检验的SPSS实现)。

(三) 统计描述及推断

1. 软件操作

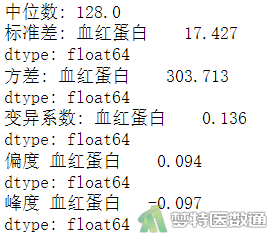
#描述性统计分析#

print('中位数:',round(np.median(df2),3))  #计算中位数
print('标准差:',round(np.std(df2),3))  #计算标准差
print('方差:',round(np.var(df2),3))  #计算方差
cv = np.std(df2)/np.mean(df2)  
print('离散系数:',round(cv,3))  #计算变异系数
print('偏度',round(df2.skew(axis = 0),3) )  #计算偏度
print('峰度',round(df2.kurtosis(axis = 0),3) )  #计算峰度

#单样本t检验#

t,p=stats.ttest_1samp(df2, popmean = 145)   #进行单样本t检验
print("t-values=",t)  #输出t统计量
print("p-values=",p) #输出概率P
if p < 0.05:    #概率P与显著水平α比较
       print("差异显著") 
else:
       print("差异不显著")

#计算均值差#

aa = 145
bb = np.mean(df2.血红蛋白)  
print('特殊作业男性血红蛋白均值:',bb) 
junzhicha = bb - aa    
print('均值差:',junzhicha)

#计算均值的置信区间#

from scipy import stats
t_ci=2.009
sample_mean=df2['血红蛋白'].mean()
se=stats.sem(df2['血红蛋白'])
a=sample_mean-t_ci*se
b=sample_mean+t_ci*se
print('特殊作业男性的血红蛋白均数的置信区间，95置信水平 CI=[%f,%f]'%(a,b))

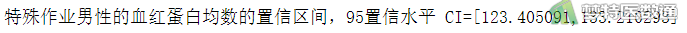
#计算差值的置信区间#

a1=junzhicha-t_ci*se
b1=junzhicha+t_ci*se
print('差值的置信区间，95置信水平 CI=[%f,%f]'%(a1,b1))

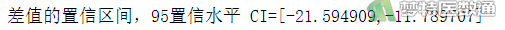
2. 结果解读

(1) 统计描述

由图3、图7可知研究案例的“counts (样本量)”“mean (均数)”“std (标准差)”“var (方差)”“np.std()/np.mean() (离散系数)”“Min (最小值)”“1st Qu (P₂₅)”“Median (中位数)”“Mean (平均值)” “3rd Qu (P₇₅)”和“Max (最大值)”“skew (偏度)”和“kurtosis (峰度)”。可知样本人群的血红蛋白含量为128.308±17.597g/L。

(2) 统计学推断

图9、图10、图11 stats.ttest_1samp (单样本t检验)”运行结果中提供了统计学推断的“t (统计量t值)”、“p-value (P值)”、推断结果、变量的均值及“95 percent confidence interval (95%置信区间，95%CI)”。可知样本人群的血红蛋白含量平均值与正常人群之间的差异有统计学意义(t=-6.8402，P<0.001)。目标人群的血红蛋白含量比正常人群平均低16.692 (95%CI：-21.595~-11.790)。

四、结论

本研究采用单样本t检验判断某特殊作业成年男性工人的血红蛋白含量是否与正常成年男性有差异。通过专业知识判断，数据不存在需要处理的异常值；通过绘制Q-Q图和Shapiro-Wilk检验，提示数据服从正态分布。

结果显示，某特殊作业成年男性人群的血红蛋白含量为128.308±17.597g/L，与正常成年男性人群血红蛋白均值145g/L的差值为16.692 (95%CI：-21.595~-11.790)。单样本t检验提示，样本人群的血红蛋白含量低于正常成年男性，差异有统计学意义(t=-6.8402，P<0.001)。本研究结果提示某特殊作业成年男性工人的血红蛋白含量低于正常成年男性。