单因素方差分析可比较两个或以上总体的平均值整体是否存在差异,还可以进一步比较以确定其中一个平均值与其他不同。在实际工作中,常需要更多的备择假设,例如:检验处理组平均值是否与对照组平均值不同,剂量水平是否存在线性趋势等。此时需要特定的对比进行检验,即比较加权平均值,当权重之和等于0时,比较称为对比。本文将介绍单因素方差分析对比法(One-Way Analysis of Variance Contrast)的样本量计算,其样本量计算具体过程及注意事项如下。
一、案例数据
某大学营养与食品卫生研究所欲研究某受试物培养基对果蝇寿命的影响,拟采用完全随机设计的方差分析。分别以浓度0%、0.022%、0.067%的某受试物培养基进行培养,观察果蝇存活时间。研究者主要关注浓度为0.022%、0.067%时的处理组是否与对照组浓度(0%)时不同,因此,需检验的对比表示为系数“-2,1,1”,对照组和处理组果蝇平均生存的时间分别为65天、66天、66.8天。以往研究的标准差为8.42,若各组样本含量相等,取α=0.05、β=0.10,试估计所需的样本含量?
二、案例分析
浓度0%、0.022%、0.067%的培养基为三种不同组别,评价指标为果蝇平均生存时间,欲检验处理组果蝇平均生存时间是否与对照组(0%)果蝇平均生存时间不同,宜采用单因素方差分析对比法。单因素方差分析对比估算样本含量,需要以下几个参数:
1. 组别数,表示需要比较的组别数。
2. 平均数,即各组的平均数,本例为果蝇平均生存时间。
3. 标准差σ,表示相同处理中对象与对象间的变异。
4. 检验水准α (通常取0.01至0.1,本例取0.05)。
5. 检验功效1-β (通常为0.80或更高,本研究取0.90)。
6. 脱失率DR (通常不宜超过20%,本例取10%)。
三、软件操作
(一) 方法选择
在左侧界面中依次选择“Procedures (程序)”—“Means (平均值)” —“One-Way Designs (ANOVA) (单因素方差分析设计)”— “ANOVA F-Test”(方差分析F检验)— “One-Way ANOVA Contrasts (单因素方差分析对比)”,见图1。

(二) 参数设置
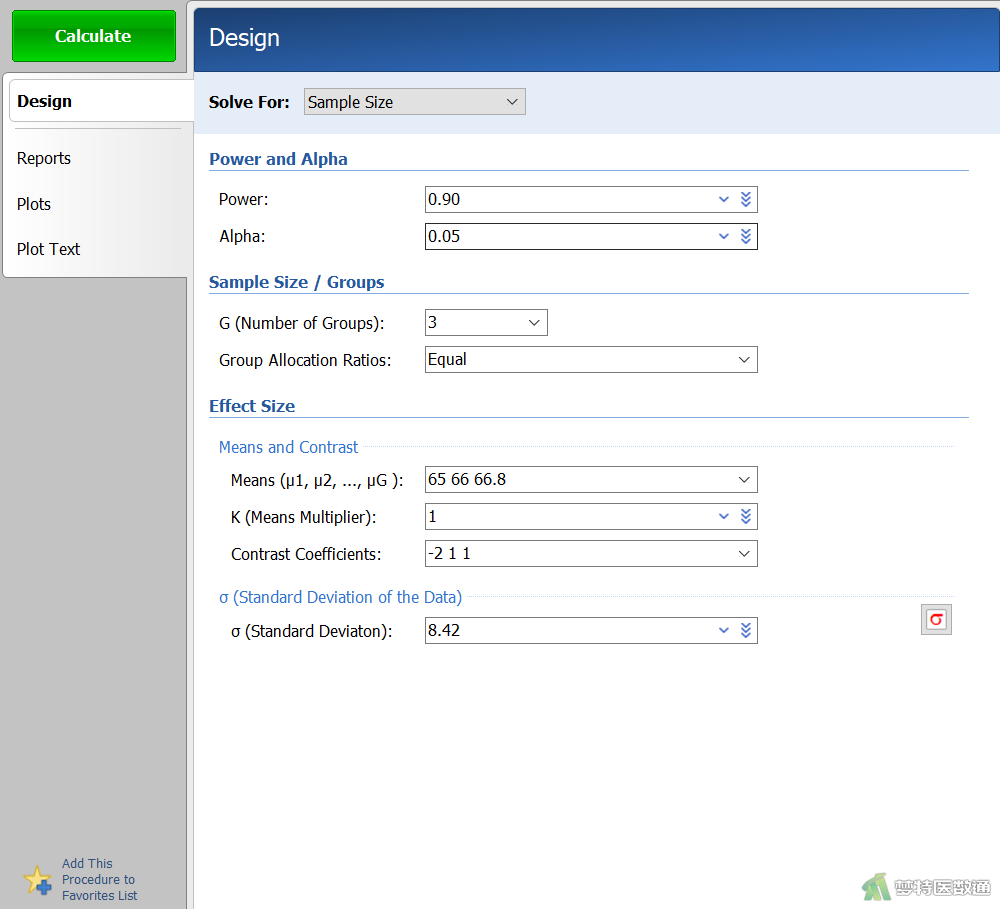
在“Design (设置)”模块中按以下参数设置相应选项(图2):
①Solve For:选择“Sample Size”,表示本分析的目的是用于计算样本量。
② Power and Alpha:Power为把握度,填写“0.90”;Alpha为检验水准,填写“0.05”。
③Sample Size/Groups:“G (Number of Groups)”设定准备比较的组平均值个数G,G必须≥2,本例填“3”;“Group Allocation Ratios”表示每组样本量分配的比例,本例选择“Equal”,即每组样本含量相等。
④Effect Size:“Means (u1,u2,....uG)”各组的平均值,本例填写“65 66 66.8”;“K (Mean Multiplier)”输入平均值倍数K,当输入多个K值时,对每个K值进行单独的分析,通过这种方式可以确定检验功效对平均值的敏感性,本例填写“1”;“Contrast Coefficients”表示对比系数,PASS里有如下选项:“None”表示忽略该选项、“Linear Trend”表示平均值呈线性趋势、“Quadratic”表示平均值服从二次模型、“Cubic”表示平均值服从三次模型、“First Against Others”表示第一组的平均值与剩余的平均值的平均数不同、“List of Coefficents”自行输入系数。值得注意的是,所有系数之和必须为0,本例填“-2 1 1”。
⑤σ (Standard Deviation):输入组内对象间的标准差σ,σ表示相同处理组中对象与对象间的变异,方差分析假设所有分组的σ相等。该值必须为正数,本例填“8.42”。
(三) 脱失率设置
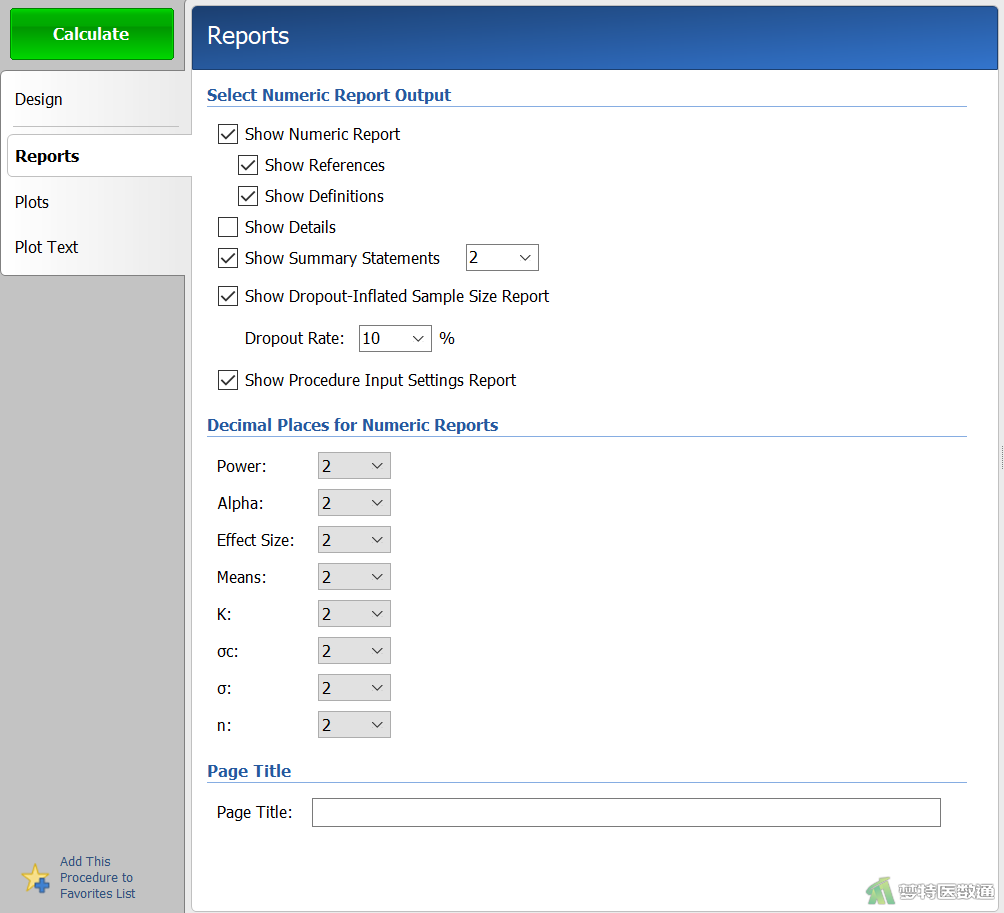
在“Reports (结果报告)”模块中,勾选“Show Dropout-Inflated Sample Size Report (报告脱失样本量)”,在“Dropout Rate”中填写“10%”(图3),表示按照10%的脱失率计算样本量。设置好上述参数后点击“Calculate (计算)”。
四、结果及解释
图4列出了该研究设计的相关参数和样本量计算结果,可知共需要1713只果蝇,其中N1=N2=N3=571。

图5“References (参考文献)”列出了该计算过程中参考的相关文献;“Report Definitions (报告定义)”列出了各个参数的具体解释;“Summary Statements (报告概述)”为整个分析报告的摘要。

图6“Dropout-Inflated Sample Size (脱失样本量)”为考虑了脱失率的样本量(N'),也是研究实际开展过程中需要达到的最低样本量,共需要1905只果蝇,其中N1‘=N2’=N3‘=635。

图7为此次样本量估算整个过程的详细参数设置汇总。

五、结论
该案例为单因素方差分析对比法进行样本量计算。已知浓度0%、0.022%、0.067%某受试物培养基培养的果蝇生存时间分别为65天、66天、66.8天,以往研究的标准差为8.42。要比较浓度为0.022%、0.067%时的处理组是否与对照组浓度(0%)时不同,取α=0.05、β=0.10,则至少需要1713只果蝇,其中N1=N2=N3=571。若考虑10%的脱失率,则至少需要1905只果蝇,其中N1’=N2‘=N3’=635。