在前面文章中我们分别介绍了Friedman检验的假设检验理论,本篇文章将使用实例演示在R软件中实现Friedman检验的操作步骤。
关键词:R语言; R软件; 非参数检验; 秩和检验; Friedman检验; 重复测量非参数检验
一、案例介绍
8名受试对象在相同试验条件下分别接受A、B、C 3种不同频率振动的刺激,测量其反应率(%),问3种频率振动刺激的反应率是否有差别? 部分数据见图1。本文案例可从“附件下载”处下载。
二、问题分析
本案例的分析目的是判断多组相关数据的差异,首先对三组数据进行正态性检验,若发现不符合正态分布,可以使用Friedman检验。Friedman检验可应用于多组配对或相关数据的秩转换非参数检验,但需要满足两个条件:
条件1:观察变量为连续变量或有序分类变量。本研究中反应率为连续变量,该条件满足。
条件2:观察变量具有3个及以上的分组,为配对设计,或各组之间存在相关性。本研究中3组数据均是对同一批研究对象所测量,该条件满足。
三、软件操作及结果解读
(一) 导入数据
mydata <- read.csv("Friedman检验.csv") #导入CSV数据
View(mydata) #查看数据
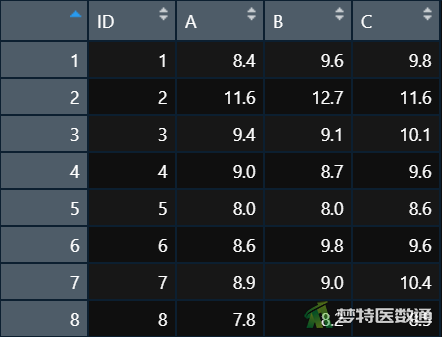
在数据栏目中可以查看全部数据情况,数据集中共有4个变量和8个观察数据,4个变量分别代表被调查者的编号(ID)以及三种不同频率震动的刺激(A、B、C)。
如果数据集较大也可使用如下命令查看数据框结构:
str(mydata) #查看数据框结构
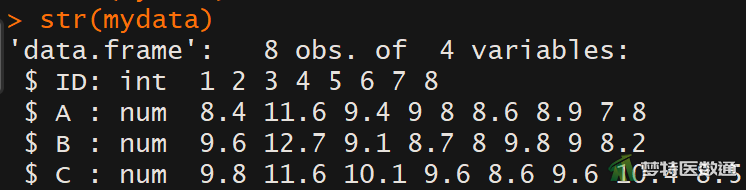
(二) 适用条件判断
1. 软件操作
## 绘制Q-Q图 ## par(mfrow = c(1, 3)) #设置画1行3个图片 qqnorm(mydata$A, main="A") #绘制A的qq图 qqline(mydata$A) #增加趋势线 qqnorm(mydata$B, main="B") #绘制B的qq图 qqline(mydata$B) #增加趋势线 qqnorm(mydata$C, main="C") #绘制C的qq图 qqline(mydata$C) #增加趋势线
## 正态性检验 ## shapiro.test(mydata$A) # A的shapiro-Wilk正态性检验 shapiro.test(mydata$B) # B的shapiro-Wilk正态性检验 shapiro.test(mydata$C) # C的shapiro-Wilk正态性检验
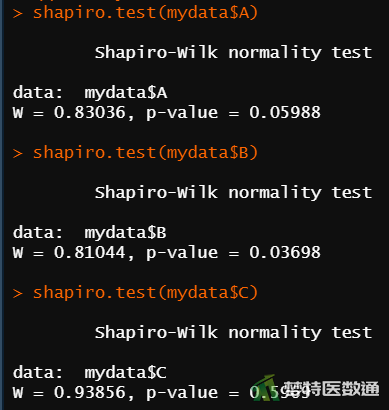
2. 结果解读
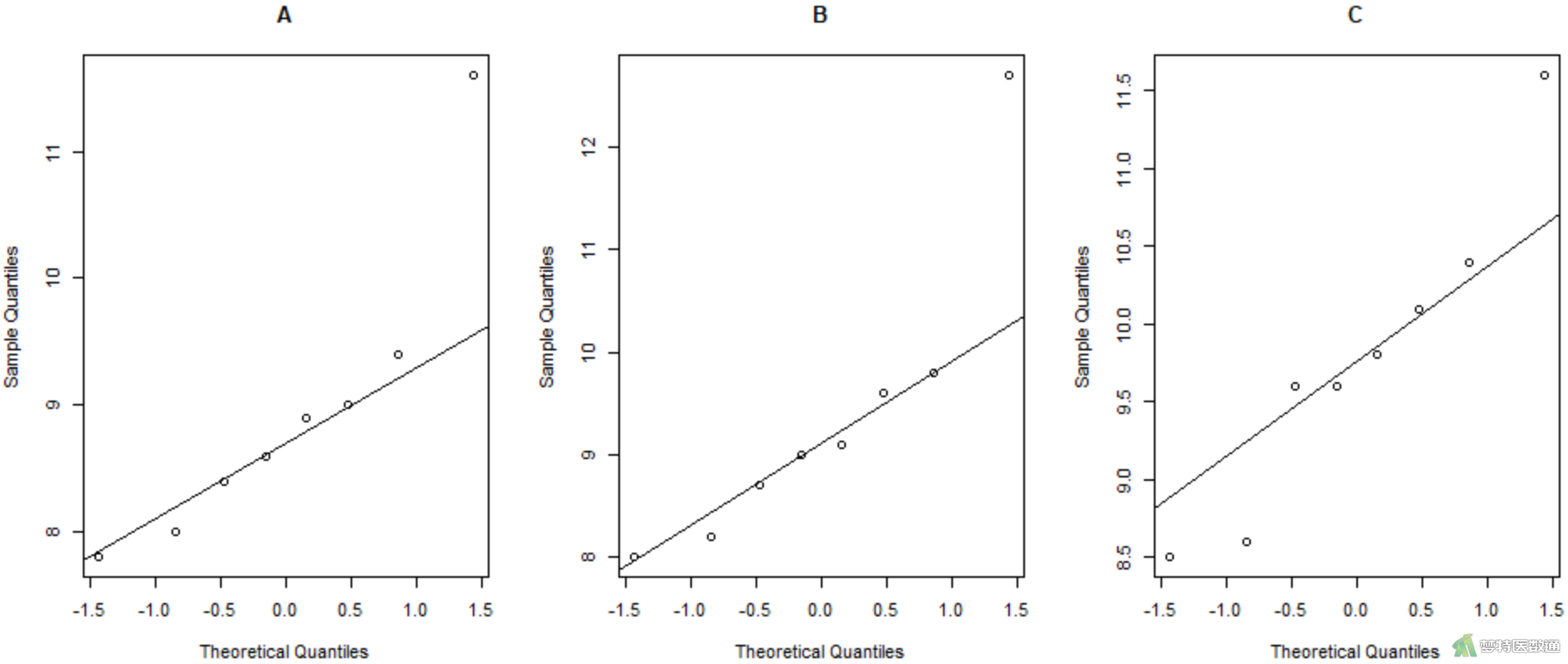
图3的Q-Q图上三组散点偏离对角线较远,尤其是A、B两组数据,提示三组数据不服从正态分布;图4的正态性检验结果显示A、B、C三组的P值分别为0.05988、0.03698和0.5969,前两组P值均<0.1,也提示两组数据不满足正态性条件。因此,本案例应使用Friedman检验比较三组反应率的差异。关于正态性检验的注意事项详见文章医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现。
(三) 整体检验
1. 统计描述
(1) 软件操作
## 描述性统计 ## summary(mydata$A) #描述A组基本情况 summary(mydata$B) #描述B组基本情况 summary(mydata$C) #描述C组基本情况
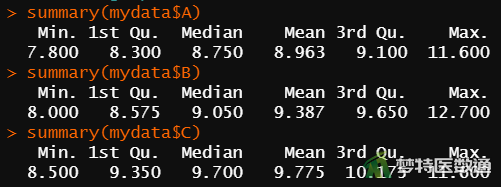
(2) 结果解读
图5“summary (描述性分析)”提供了三组数据的“Min.(最小值)”、“1st Qu.(P25)”、 “Median(中位数)、“Mean(平均值)”、 “3rd Qu.(P75)”和“Max.(最大值)。可知,受试者对A频率振动的反应率为8.750% (P25~P75:8.300%~9.100%);对B频率振动的反应率为9.050% (P25~P75:8.575%~9.650%);对C频率振动的反应率为9.700% (P25~P75:9.350%~10.175%)。
2. 整体检验
(1) 软件操作
## 统计推断 ## mydata2<-as.matrix(mydata) #数据转换为矩阵格式 mydata3<-mydata2[,c(2,3,4)] #去除第一列无用数据 friedman.test(mydata3) #friedman检验
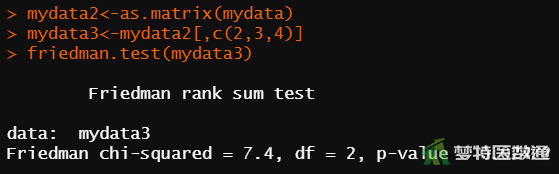
(2) 结果解读
图6显示了Friedman检验的结果。由“Friedman”结果可知,χ²=7.4, P = 0.02472,差异有统计学意义。即3种频率振动刺激的反应率总体比较差别具有统计学意义(P < 0.05) (至少存在两组不相同)。
(四) 事后检验(两两比较)
虽然得到了“3种频率振动刺激的反应率总体比较差别具有统计学意义”的结论,但若要清楚了解到底是哪些频率刺激的反应率不同,则需要进一步进行两两比较。
1. 软件操作
## 事后检验 ## library(PMCMR) #调用程序包“PMCMR” posthoc.friedman.nemenyi.test(mydata3)
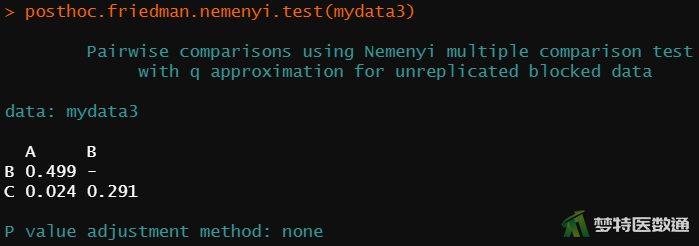
2. 结果解读
图7两两比较结果显示,频率A和频率B的差异无统计学意义(P=0.499),频率A和频率C的差异有统计学意义(P=0.024),频率B和频率C的差异尚无统计学意义(P=0.291)。
四、结论
本案例欲比较在A、B、C 3种不同频率振动的刺激下受试者的反应率(%)是否存在差异。通过绘制Q-Q图和Shapiro-Wilk检验,提示数据不服从正态分布,故采用Friedman检验对数据进行分析。
结果显示,受试者对A、B、C 3种不同频率振动的刺激反应率(%)分别为8.750%(P25~P75:8.300%~9.100%)、9.050% (P25~P75:8.575%~9.650%)、9.700% (P25~P75:9.350%~10.175%),差异有统计学意义(χ²=7.4,P = 0.02472)。进一步两两比较显示,频率A和频率B的差异无统计学意义(P=0.499),频率A和频率C的差异有统计学意义(P=0.024),频率B和频率C的差异尚无统计学意义(P=0.291)。