在前面文章中介绍了两因素方差分析(Two-way ANOVA)——不存在交互作用时在SAS软件中的实现,本篇文章将实例演示在SAS软件中实现两因素方差分析——存在交互作用时的操作步骤。
关键词:SAS; 两因素方差分析; 交互作用; 主效应; 单独效应; 简单效应
一、案例介绍
观察A、B两种镇痛药物联合运用在产妇分娩时的镇痛效果。A药(Drug_A)取3个剂量:1.0、2.5、5.0 mg;B药(Drug_B)也取3个剂量:5.0、15.0、30.0μg,共9个处理组。将27名产妇随机分成9组,每组3名产妇,记录每名产妇分娩时的镇痛时间Time (min)。试分析A、B两药联合运用的镇痛效果。
创建代表处理因素的变量“Drug_A”和“Drug_B”, “Drug_A”赋值为“1”、“2”、“3”分别代表1.0、2.5、5.0 mg三个剂量,“Drug_B”赋值为“1”、“2”、“3”分别代表5、15、30 μg三个剂量。创建观察变量“Time”,记录各处理组中每名对象的镇痛时间。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析
本案例的分析目的是分析A、B两种药物联合运用的镇痛效果。临床上,药物之间联合运用往往会相互影响,这种影响可能为正向的增强效应,也可能为反向的拮抗作用。针对这种情况,可以使用多因素方差分析,由于本案例为药物A和药物B两个因素,因此可以使用两因素方差分析。但需要满足6个条件:
条件1:观察变量唯一,且为连续变量。本研究中观察变量只有镇痛时间,且为连续变量,该条件满足。
条件2:有两个因素,且都为分类变量。本研究中有A、药物B物两个因素,都为分类变量,该条件满足。
条件3:观测值之间相互独立。本研究中各研究对象的观测值都是独立的,不存在互相干扰的情况,该条件满足。
条件4:观察变量不存在显著的异常值,该条件需要通过软件分析后判断。
条件5:各组、各水平观测值为正态(或近似正态)分布,该条件需要通过软件分析后判断。
条件6:相互比较的各处理水平(组别)的总体方差相等,即方差齐同,该条件需要通过软件分析后判断。
三、软件操作及结果解读
由于本案例组别较多且每组观察数很少,所以使用残差检查异常值、正态性及方差齐性。
(一) 导入数据
①利用LIBNAME语句建立SAS逻辑库关联,注意逻辑库名称要求,即最大长度8字符,必须以字母或下划线“_”开始,可以是字母、数字和下划线的任意组合。具体代码如下:
libname mydata 'D:\mydata';
通过这一步骤,SAS能够识别引号中的物理位置,将逻辑库建立在该目录下,同时在以下过程中新建的SAS表格便可以永久储存在该位置,便于反复读取和使用。先运行该代码使其生效。
②利用PROC IMPORT语句导入文件,代码如下:
proc import out= mydata.example datafile=" D:\mydata\两因素方差分析2.csv " dbms=csv replace; getnames=yes; run;
该过程在mydata逻辑库中生成example数据集,数据文件由DATAFILE=选项指定,DBMS=选项指定其数据库类型。该案例中初始数据集为csv文件,故而使用“dbms=csv”指定。如果已经存在相同名称的SAS数据集,即可使用REPLACE选项进行覆盖。GERNAMES=YES选项指定从第2行开始读取数据,将数据集的首行变量名作为SAS数据集的变量名。
(二) 适用条件判断
1. 生成因变量残差
(1) 软件操作
①运用SORT过程以Drug_A、Drug_B升序排列的形式重新排列,具体代码如下所示:
Proc sort data=mydata.example; by Drug_A Drug_B; run;
重新排列后数据如图2所示:

②运用REG过程计算残差,具体代码如下所示:
Proc reg data=mydata.example; by Drug_A Drug_B; model time= Drug_A Drug_B /r; output out=mydata.example2 r=residual; run; quit;
BY语句以“Drug_A”和“Drug_B”变量分组计算残差,MODEL语句以“time”为因变量,“Drug_A”和“Drug_B”作为分组变量计算残差的值。OUTPUT语句将残差输入新建的表“mydata.example2”,新建变量命名为“residual”。“r=residual”将该步骤中计算得的残差输入至新表。
(2) 结果解读
上述操作将可以得到生成的新变量“residual”,如图3所示。

2. 条件4判断(异常值判断)
(1) 软件操作
①运用UNIVARIATE语句进行检验,具体代码如下所示:
proc univariate data=mydata.example2 normal plot; class Drug_A Drug_B; var residual; run;
CLASS语句起到拆分文件的作用,分别分析“Drug_A”和“Drug_B”分别为“1”“2”“3”时共9个处理组是否存在异常值。PLOT选项可作各分组的平行条状图,箱线图和正态概率图。“Drug_A”=1且“Drug_B”=1时如图4所示,其余图像不一一列举。

②运用ANOVA过程作各组箱式图,具体代码如下所示:
proc anova data = mydata.example2; class Drug_A Drug_B; model residual = Drug_A*Drug_B; means Drug_A*Drug_B / hovtest=levene(type=abs); run;
该步骤中,CLASS语句指定分类变量,即“Drug_A”和“Drug_B”两变量。MODEL语句指定分析因素与响应变量,即按照“Drug_A”和“Drug_B”同时分组对“residual”变量分析。该过程输出结果如图5所示,图中显示的横坐标“Drug_A*Drug_B”即表示“Drug_A”和“Drug_B”分别为“1”“2”“3”时共9个处理组的箱式图。

(2) 结果解读
图5残差的箱线图未提示任何异常值和极端值,满足条件4。
3. 条件5判断(正态性检验)
两因素方差分析时,可分别考察每一组原始数据的正态性或使用残差考察整体正态性。
(1) 软件操作
运用UNIVARIATE语句对残差考察整体正态性,具体代码如下所示:
proc univariate data=mydata.example2 normal plot; var residual; run;
NORMAL选项可以对进行整体残差的正态性检验。PLOT选项可以得到平行条状图,箱线图和正态概率图。
(2) 结果解读
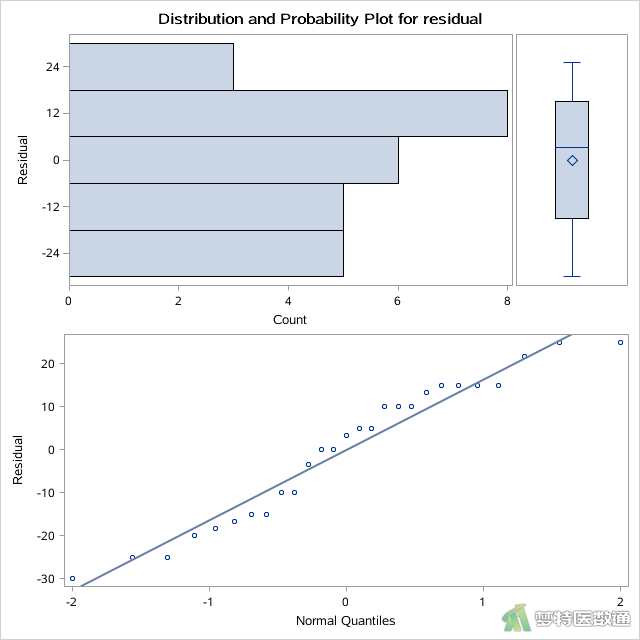
图6显示了四种正态性检验的结果,Shapiro-Wilk (夏皮罗-威尔克正态性,S-W)检验和Kolmogorov-Smirnov (柯尔莫哥洛夫-斯米诺夫,K-S)检验。K-S检验适用于大样本资料,本案查看S-W检验结果,可见P值>0.1,提示整体残差服从正态分布。
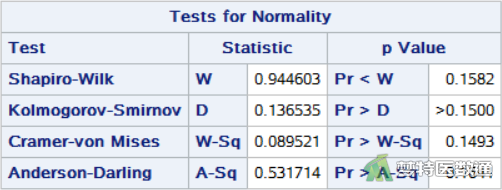
图7为整体残差正态性检验的正态概率图,可见散点基本围绕对角线分布,也提示数据服从正态分布。综上,本案例满足条件5。
4. 条件6判断(方差齐性检验)
(1) 软件操作
运用ANOVA过程进行检验,具体代码如下所示:
proc anova data = mydata.example2; class Drug_A Drug_B; model time = Drug_A*Drug_B; means Drug_A*Drug_B / hovtest=levene(type=abs); run;
该步骤中,CLASS语句指定分类变量,即“Drug_A”和“Drug_B”两变量。MODEL语句指定分析因素与响应变量,即按照“Drug_A”和“Drug_B”同时分组对“time”变量分析。 MEANS语句计算均数和方差,其常见选项HOVTEST可指定分析方法,此处我们使用LEVENE检验,“(type=abs)”指定该过程计算绝对值(absolute value)进行分析。
(2) 结果解读
图8“Levene's Test for Homogeneity (Levene’s方差齐性检验)”的结果显示,统计量F=0.70、P=0.6912;提示数据总体方差相等。本案例满足条件6。
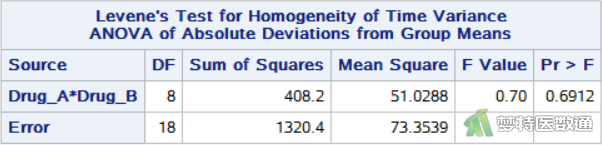
(三) 统计描述及推断
1. 软件操作
①前一步骤中UNIVARIATE语句可得各组数据的统计描述结果。也可用MEANS过程,其代码如下:
proc means data = mydata.example2; class Drug_A Drug_B; var time; run;
②运用ANOVA过程进行检验,该过程与上述ANOVA过程稍有不同,具体代码如下所示:
proc anova data = mydata.example2; class Drug_A Drug_B; model time = Drug_A|Drug_B; means Drug_A|Drug_B /snk; run;
该过程中使用“Drug_A|Drug_B”,可以对两变量的交互作用进行检验,其也可以替换为“Drug_A Drug_B Drug_A*Drug_B”。SNK法指定两两比较方法。
2. 结果解读
(1) 统计描述
图9是由MEANS过程所得的“Descriptives Statistics(描述统计)”列出了各组的均值和标准差,可知A药在1.0 mg水平,B药为5.0、15.0、30.0 μg水平时,镇痛时间分别为:83.33±20.21、100.00±18.03、85.00±10.00 min;A药在2.5 mg水平,B药为5、15、30 μg水平时,镇痛时间分别为:90.00±21.79、115.00±21.79、135.00±15.00 min;A药在5.0 mg水平,B药为5、15、30 μg水平时,镇痛时间分别为:110.00±21.79、95.00±27.84、176.67±15.28 min。ANOVA过程给出time分布的箱线图,如图10所示。


(2) 统计推断
图11 为ANOVA过程输出结果,显示了对所假设的模型进行方差分析的结果,原假设为模型中所有的影响因素均无作用,即A药、B药、两者的交互作用均对镇痛时间无影响。第一行的“Corrected Model(修正模型)”即对所假设的模型进行检验的结果,F=6.92,P=0.0003,因此所用的模型有统计学意义,以上所提到的影响因素中至少有一个对镇痛时间有影响,但具体是哪些需看后续分析结果。

(3) 交互作用判断
由于本案例有两个因素(一个为A药,另一个为B药),首先需要判断两个药物之间是否存在交互作用。如果交互作用有统计学意义,则需要分析单独效应。
图10第三行是对A药和B药交互作用的判断,FDrug_A*Drug_B=5.07,P值为0.0065,有统计学意义,说明两者存在交互作用。
(四) 单独效应分析
1. 软件操作
proc glm data = mydata.example2; class Drug_A Drug_B; model time = Drug_A Drug_B Drug_A*Drug_B; lsmeans Drug_A *Drug_B /slice=Drug_B; run; quit;
更改lsmeans Drug_A /slice=Drug_B中变量名顺序,对不同的A药浓度下分析B药的作用,具体代码如下:
proc glm data = mydata.example2; class Drug_A Drug_B; model time = Drug_A Drug_B Drug_A*Drug_B; lsmeans Drug_A*Drug_B /slice=Drug_A; run; quit;
2. 结果解读
(1) A药的单独效应
A药的单独效应就是在不同的B药浓度下分析A药的作用。由图10可大致看出,在不同的B药浓度下,A药对镇痛时间的影响不同,具体的检验结果见图12。结果显示,在药物B为5.0 μg水平时,药物A各水平之间的镇镇痛时间差异无统计学意义(F=1.49,P=0.252);在药物B为15.0 μg水平时,药物A各水平之间的镇镇痛时间差异无统计学意义(F=0.84,P=0.449);但在药物B为30.0 μg水平时,药物A各水平之间的镇镇痛时间差异有统计学意义(F=16.29,P<0.001)。

(2) B药的单独效应
由图10可大致看出,在不同的A药浓度下,B药对镇痛时间的影响不同,具体的检验结果见图13。结果显示,在药物A为1.0 mg水平时,药物B各水平之间的镇痛时间差异无统计学意义(F=0.65,P=0.533);在药物A为2.5 mg水平时,药物B各水平之间的镇痛时间差异有统计学意义(F=3.93,P=0.038);但在药物A为5.0 mg水平时,药物B各水平之间的镇痛时间差异有统计学意义(F=14.61,P<0.001)。

(五) 事后检验(两两比较)
1. 软件操作
ods output Estimates=estimate;
proc glm data = mydata.example2;
class Drug_A Drug_B;
model time =Drug_A Drug_B Drug_A*Drug_B;
estimate '(Drug_A 1.0mg vs 2.5mg)/Drug_B=30ug' Drug_A 1 -1 0 Drug_A*Drug_B 0 0 1 0 0 -1 0 0 0;
estimate '(Drug_A 1.0mg vs 5.0mg)/Drug_B=30ug' Drug_A 1 0 -1 Drug_A*Drug_B 0 0 1 0 0 0 0 0 -1;
estimate '(Drug_A 2.5mg vs 5.0mg)/Drug_B=30ug' Drug_A 0 1 -1 Drug_A*Drug_B 0 0 0 0 0 1 0 0 -1;
estimate '(Drug_B 5.0ug vs 15.0ug)/Drug_A=2.5mg' Drug_B 1 -1 0 Drug_A*Drug_B 0 0 0 1 -1 0 0 0 0;
estimate '(Drug_B 5.0ug vs 30.0ug)/Drug_A=2.5mg' Drug_B 1 0 -1 Drug_A*Drug_B 0 0 0 1 0 -1 0 0 0;
estimate '(Drug_B 15.0ug vs 30.0ug)/Drug_A=2.5mg' Drug_B 0 1 -1 Drug_A*Drug_B 0 0 0 0 1 -1 0 0 0;
estimate '(Drug_B 5.0ug vs 15.0ug)/Drug_A=5mg' Drug_B 1 -1 0 Drug_A*Drug_B 0 0 0 0 0 0 1 -1 0;
estimate '(Drug_B 5.0ug vs 30.0ug)/Drug_A=5mg' Drug_B 1 0 -1 Drug_A*Drug_B 0 0 0 0 0 0 1 0 -1;
estimate '(Drug_B 15.0ug vs 30.0ug)/Drug_A=5mg' Drug_B 0 1 -1 Drug_A*Drug_B 0 0 0 0 0 0 0 1 -1;
run;
quit;
proc print data=estimate;run;
data estimate;
set estimate;
Probt=Probt*3;/* 通过“Bonferroni (邦弗罗尼)”法两两比较*/
proc print;run;
2. 结果解读

图14为B药30 µg浓度下,A药的两两检验结果和A药在2.5 mg和5 mg情况下,B药的两两检验结果,提供了不同浓度间两两比较的“LSMEAN (最小二乘均值)”和各组相比的“Pr (P值)”。
由之前结果可知,当B药为5 μg与15 μg 时,A药整体无统计学意义(P>0.05),故这里不再分析。当B药为30 μg时, A药浓度为2.5 mg和5.0 mg与1.0 mg相比,均值差逐渐增大。2.5 mg比1.0 mg时均值增加了50.00 min,差异有统计学意义(P=0.0182);至5.0 mg时增加了91.67 min,差异有统计学意义(P<0.0001);2.5 mg到5.0 mg时增加了41.67 min,差异无统计学意义(P=0.0554)。表明,在B药为30.0 μg水平时,随着A药浓度的增加,镇痛时间呈上升趋势。
当A药为1.0 mg时,B药整体无统计学意义(P>0.05),这里不再比较。当药物A为2.5 mg时,药物B浓度30.0 μg与5.0 μg相比,镇痛时间差异有统计学意义(P=0.036),30.0 μg与15.0 μg相比以及15.0 μg与5.0 μg相比差异均无统计学意义(P>0.05)。当药物A为5.0 mg时,药物B浓度30.0 μg与15.0 μg相比以及30.0 μg与5.0 μg相比,镇痛时间差异均有统计学意义(P<0.01),但15.0 μg与5.0 μg相比,镇痛时间差异无统计学意义(P=1.090)。
四、结论
本研究采用两因素方差分析探讨A、B两种镇痛药物联合运用在产妇分娩时的镇痛效果。通过对模型残差绘制箱线图提示,数据不存在异常值;通过Shapiro-Wilk检验,提示各组数据服从正态分布;通过Levene’s检验,提示数据总体方差相等;两药物之间存在交互作用(FDrug_A*Drug_B=5.073,P=0.006),故进行简单效应分析。
药物A在1.0 mg水平,药物B为5.0、15.0、30.0 μg水平时,镇痛时间分别为:83.333±20.207、100.000±18.028、85.000±10.000 min;药物A在2.5 mg水平,药物B为5、15、30 μg水平时,镇痛时间分别为:90.000±21.794、115.000±21.794、135.000±15.000 min;药物A在5.0 mg水平,药物B为5、15、30 μg水平时,镇痛时间分别为:110.000±21.794、95.000±27.839、176.667±15.275 min。
药物A的简单效应分析显示,在药物B为30.0 μg水平时,药物A各水平之间的镇痛时间差异有统计学意义(F=16.29,P<0.001)。但在药物B为5.0 μg和15.0 μg水平时,药物A各水平之间的镇痛时间差异均无统计学意义(P>0.05)。对药物A在药物B为30.0 μg水平时进行“Bonferroni (邦弗罗尼)”法两两比较结果显示, 1.0 mg至2.5 mg时均值增加了50.00 min,至5.0 mg时均值增加了91.67 min,差异均有统计学意义(P<0.001);表明,在药物B为30.0 μg水平时,随着药物A浓度的增加,镇痛时间呈上升趋势。
药物B的简单效应分析显示,在药物A为1.0 mg水平时,药物B各水平之间的镇痛时间差异无统计学意义(F=0.65,P=0.533);但在药物A为2.5 mg和5.0 mg水平时,药物B各水平之间的镇痛时间差异均有统计学意义(P<0.05)。“Bonferroni (邦弗罗尼)”法两两比较显示,当药物A为2.5 mg时,药物B浓度30.0 μg与5.0 μg相比,镇痛时间差异有统计学意义(P=0.036),30.0 μg与15.0 μg相比以及15.0 μg与5.0 μg相比差异均无统计学意义(P>0.05)。当药物A为5.0 mg时,药物B浓度30.0 μg与15.0 μg相比以及30.0 μg与5.0 μg相比,镇痛时间差异均有统计学意义(P<0.01),但15.0 μg与5.0 μg相比,镇痛时间差异无统计学意义(P=1.000)。
综上可知,对产妇分娩时镇痛,A、B两种药物联合运用时会相互影响,随着药物浓度的增加,联合作用趋于复杂和不稳定。
五、分析小技巧
- 正态性检验:两因素或多因素方差分析时,有两种选择来测试正态性:如果每组有较多观察数,且组别较少时,可使用原始数据检查每个组的正态性。如果有很多组,或每个组的观察数很少,可使用残差检查整体的正态性。关于正态性检验的注意事项详见(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。
- 交互作用判断:两因素方差分析时,需要首先判断两个因素之间是否存在交互作用。如果交互作用有统计学意义,则需要分析单独效应。此时,单纯研究某个因素的作用并无意义,应分别探讨另一个因素不同水平时对该因素的作用。当不存在交互作用时,说明两因素的作用彼此独立,逐一分析各因素的主效应即可;计算主效应时,在模型中仍需要保留交互项。