有序Logistic回归分析(Ordinal Logistic Regression Analysis)——R软件实现

关键词：R语言; R软件; 有序logistic回归; 有序逻辑回归; 平行性检验; 比例优势检验

一、案例介绍

在某胃癌筛查项目中，为了确定胃癌筛查的重点人群，研究者想了解首诊“胃癌分期(Stage)”与患者“经济水平(Income)”、“性别(Gender)”和“年龄(Age)”之间的关系，试对数据进行分析。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是探讨首诊“胃癌分期”与患者“经济水平”、“性别(Gender)”和“年龄(Age)”之间的关系。在案例中，首诊“胃癌分期”为因变量，有I-II期、III期、IV期、V期4个分类，且分类间有等级次序关系。因此，可以采用有序logistic回归模型进行分析。但需要满足以下5个条件：

条件1：因变量唯一，且为有序多分类变量。本研究中因变量为“胃癌分期”，且为有序多分类变量，该条件满足。

条件2：存在一个或多个自变量。本研究中有三个自变量，“性别”和“经济水平”为分类变量，“年龄”为连续变量，该条件满足。

条件3：观测值相互独立。本研究中各研究对象的观测值都是独立的，不存在互相干扰的情况，该条件满足。

条件4：自变量之间无多重共线性，该条件需要通过软件分析后判断。

条件5：满足平行性，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

mydata <- read.csv("有序logistic回归分析.csv")  #导入CSV数据
View(mydata)  #查看数据

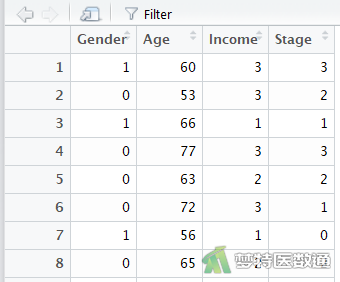
在数据栏目中可以查看全部数据情况，数据集中共有4个变量和192个观察数据，4个变量分别是“性别(Gender)”、“年龄(Age)”、“经济水平(Income)”及“胃癌分期(Stage)”。

如果数据集较大也可使用如下命令查看数据框结构：

str(mydata)  #查看数据框结构

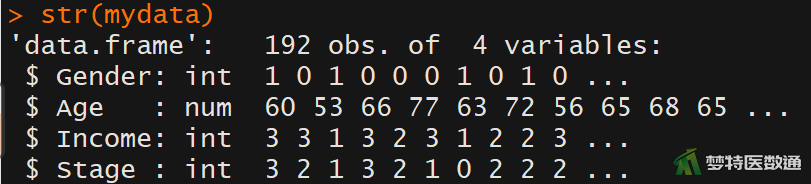
(二) 适用条件判断

1. 条件4判断(多重共线性诊断)

详见后文。

2. 条件5判断(平行性检验)

为了增加结果的可读性，给部分分类变量增加标签。

(1) 软件操作

##定义为因子，并添加标签label ##
mydata$Gender <- factor(mydata$Gender,levels = c(1,0),labels = c("male","female"))
mydata$Income <- factor(mydata$Income,levels = c(3,2,1),labels = c("high", "medium","low"))
mydata$Stage <- factor(mydata$Stage,levels = c(0,1,2,3),labels = c("I-II期","III期","IV期","V期"))
##定义参照组##
mydata$Income <-relevel(mydata$Income,ref = "low") #为经济水平设置参照组为" low "

##平行性检验##
library(VGAM) #载入包“VGAM”
om1<-vglm(Stage~Income+Age+Gender,data=mydata,
family=cumulative(parallel = T)) #按照符合平行性进行拟合
om2<-vglm(Stage~Income+Age+Gender,data=mydata,
family=cumulative(parallel = F)) #按照不符合平行性进行拟合
lrtest(om2,om1) #计算两种模型拟合结果是否一致

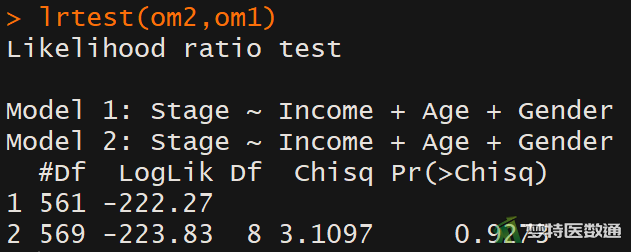
(2) 结果解读

图3展示了模型的平行性检验，平行性检验的原假设是各回归方程互相平行，χ²=3.120，P=0.927>0.05接受原假设，说明平行性假设成立，满足条件5。

(三) 变量筛选

1. 软件操作

##单因素回归分析##
library(MASS)
fit1<-polr(Stage~Gender,data=mydata)
fit2<-polr(Stage~Age,data=mydata)
fit3<-polr(Stage~Income,data=mydata)
##似然比检验##
drop1(fit1,test = "Chi")
drop1(fit2,test = "Chi")
drop1(fit3,test = "Chi")

##计算系数的可信区间##

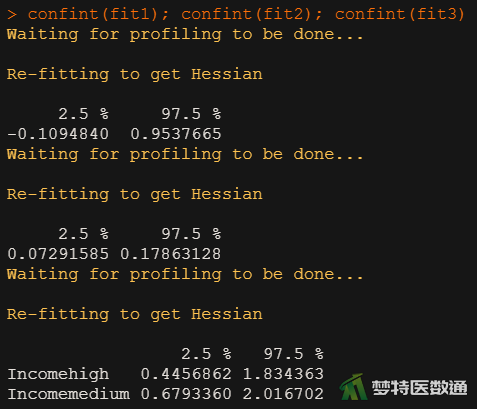
confint(fit1); confint(fit2); confint(fit3)

2. 结果解读

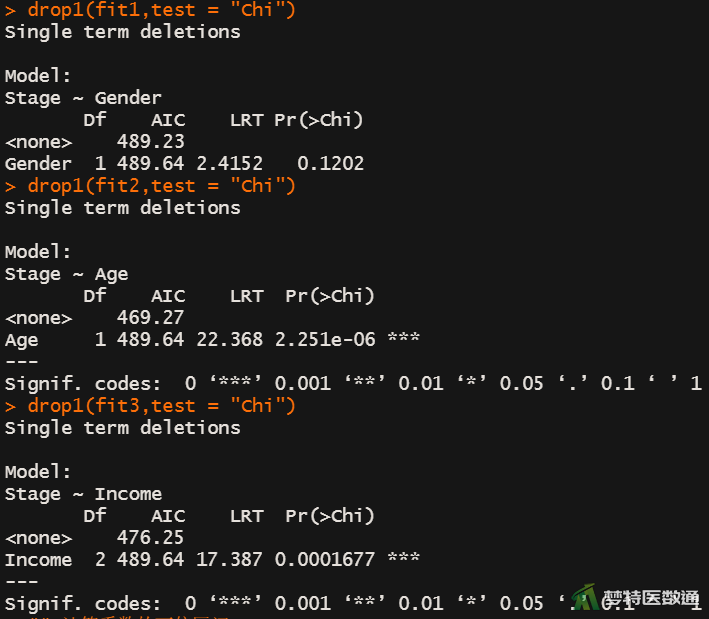
图4显示了每个单因素模型中的自变量是否有统计学意义，结果表明在单因素分析中“年龄”和“收入”与因变量的关联有统计学意义(P<0.001)，性别与因变量的关联无统计学意义(P=0.120)。图5给出了每个单因素模型中变量系数的95%CI，若置信区间包含0，则说明该变量在模型中无统计学意义；结果显示性别的95%CI包含0，其他两个变量系数的95%CI未包含0。因此，多因素回归模型中可纳入“年龄”和“收入”两个变量。

(四) 适用条件判断(补充条件5判断：多重共线性诊断)

将无统计学意义的变量“性别”移除，建立最终的回归模型后进行如下操作。

1. 软件操作

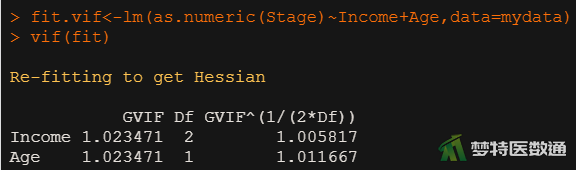
##建立新的回归模型##
fit<-polr(Stage~Income+Age,data=mydata)
##共线性诊断##
library(car) #调用包“car”
fit.vif<-lm(as.numeric(Stage)~Income+Age,data=mydata) #拟合线性回归
vif(fit.vif) #计算模型的vif

2. 结果解读 

图6中计算了自变量的方差膨胀因子(variance inflation factor，VIF)。可见，所有自变量的VIF均<10，提示自变量之间不存在严重共线性问题。满足条件5。

(五) 模型拟合

1. 软件操作

##查看变量系数##

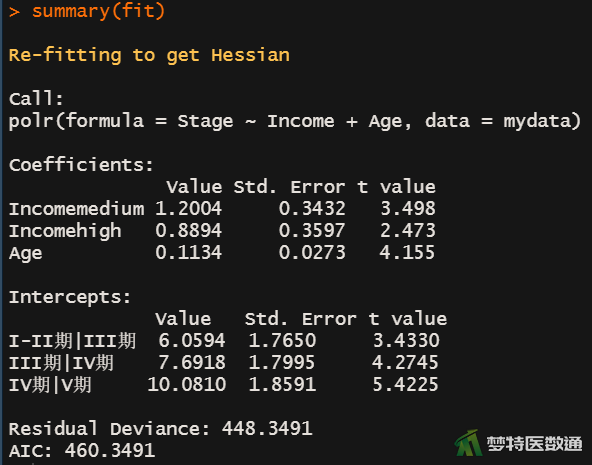
summary(fit) #模型详细结果

##计算新模型中变量系数的95%CI##

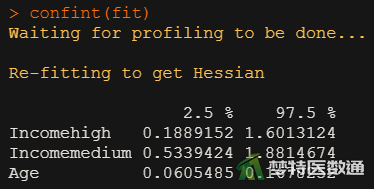
confint(fit)

##对回归系数进行检验得出P值##

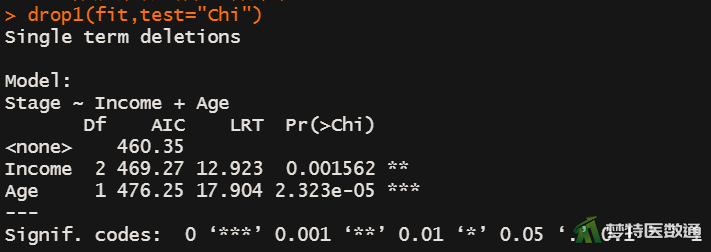
drop1(fit,test="Chi")

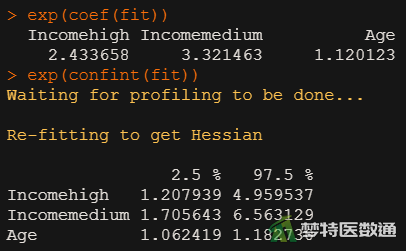
##计算新模型中的参数##
exp(coef(fit)) # 计算OR值
exp(confint(fit)) # 计算OR值的95%CI 

##模型整体检验##
##建立零模型(仅包含截距)
fit0<-polr(Stage~1,data=mydata)
##模型比较##
anova(fit,fit0)

2. 结果解读

(1) 模型系数

图7展示了模型的详细参数，Coefficients部分”列出了截距和自变量的“value (非标准化系数)”、“Std.Error (标准误)”，统计量t值。图8则显示了模型中变量系数的95%CI。图9对回归系数进行检验，图10计算了OR值及其95%CI。

其中“年龄”的P<0.001，有统计学意义；OR=1.120 (95%CI：1.062~1.183)，表示年龄每增加一岁，其首诊“胃癌分期”提升一个等级的风险是原来的1.120倍。“中等收入”水平患者首诊“胃癌分期”提升一个等级的风险是“低收入”水平患者的3.321倍(95%CI：1.706~6.563)；“高收入”水平患者首诊“胃癌分期”提升一个等级的风险是“低收入”水平患者的2.434倍(95%CI：1.208~4.960)。

(2) 拟合优度

图9给出了模型的“AIC (赤池信息量准则)”，图11给出了似然比检验的统计量和P值。由结果可知，AIC=460.35，χ²=35.292，P<0.001，所建立的模型有统计学意义。

四、结论

本研究采用有序logistic回归模型分析首诊“胃癌分期”与患者“经济水平”、“性别”和“年龄”之间的关系。因变量例数分布满足样本量需求，变量之间不存在严重共线性，满足平行性假设(χ²=3.120，P=0.927)。

“性别”对首诊“胃癌分期”的影响无统计学意义。“年龄”每增加一岁，其首诊“胃癌分期”提升一个等级的可能性是原来的1.120倍(95%CI：1.062~1.183)。“中等收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的3.321倍(95%CI：1.706~6.563)；“高收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的2.434倍(95%CI：1.208~4.960)。所建立的模型有统计学意义(χ²=35.292，P<0.001)。

五、分析小技巧

• 有序logistic回归模型分析结果除了常数项不同，各模型的自变量系数都相同。平行性检验的目的即是验证自变量不同取值对因变量的影响系数是否相同，即要满足无论因变量的分割点在什么位置，模型中各个自变量对因变量的影响不变。
• 如果不满足平行性假设，则考虑使用无序多分类logistic回归或用不同的分割点将因变量变为二分类变量，分别进行二项logistic回归。但是，当样本量过大时，平行线检验会过于敏感。即当存在平行性时，也会显示P<0.05。此时，可以尝试将因变量设置为哑变量，并拟合多个二分类logistic回归模型，通过观察自变量对各哑变量的OR值是否近似来判断。