多重线性回归分析(Multiple Linear Regression Analysis) ——R软件实现

关键词：R语言; R软件; 多重线性回归; 多元线性回归; 多重共线性; 自变量选择; 逐步回归; 模型拟合评价; 哑变量设置

一、案例介绍

某社区医师从本社区的糖尿病患者中随机抽取50名，收集了他们的性别(Gender，0=女，1=男)、经济水平(Income，1=低收入，2=中等收入，3=高收入)、空腹胰岛素(Fasting insulin，mmol/L)、糖化血清蛋白(Glycosylated serum protein)和空腹血糖(FBS，mmol/L)，欲探究空腹血糖是否受到其他几项指标的影响。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的目的是分析空腹血糖是否受到其他几项指标的影响，由于因变量是定量资料，初步考虑可使用多重线性回归分析。但需要满足以下7个条件：

条件1：样本量是自变量个数的5~10倍。本案例有4个自变量，样本量为50，满足该条件。

条件2：自变量若为连续变量，需要与因变量之间存在线性关系，可通过绘制散点图予以考察。

条件3：各观测值之间相互独立，即残差之间不存在自相关。通过研究设计和数据收集的过程分析，可判断本案例中观测值之间不存在互相影响的情况。该条件还可通过软件分析后辅助判断。

条件4：不存在显著的多变量异常值，该条件需要通过软件分析后判断。

条件5：自变量之间无多重共线性，该条件需要通过软件分析后判断。

条件6：残差符合正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件7：残差大小不随所有变量取值水平的变化而变化，即方差齐性，可通过绘制残差图进行判断。

三、软件操作及结果解读

(一) 导入数据

mydata <- read.csv("多重线性回归分析.csv")  #导入CSV数据
head(mydata)  #查看数据

在数据栏目中可以查看全部数据情况，数据集中共有5个变量和50个观察数据，5个变量分别为性别(Gender)、经济水平(Income)、空腹胰岛素(Fasting.insulin，mmol/L)、糖化血清蛋白(Glycosylated.serum.protein)和空腹血糖(FBS，mmol/L)。

如果数据集较大也可使用如下命令查看数据框结构：

str(mydata)  #查看数据框结构

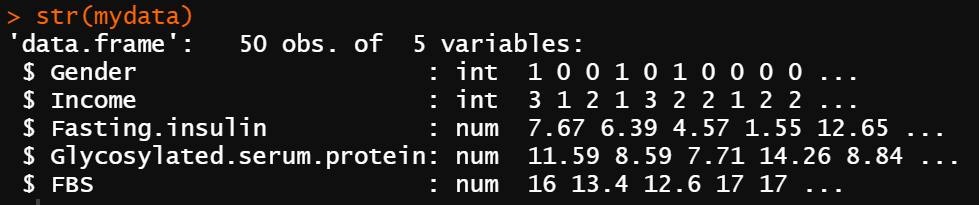
(二) 适用条件判断

1. 条件2判断(连续型自变量和因变量之间存在线性关系)

(1) 软件操作

##转换为分组变量，并添加标签##
mydata$Gender <-factor(mydata$Gender,labels = c("女","男"))
mydata$Income <-factor(mydata$Income,labels = c("低收入","中等收入","高收入")) 
##线性关系判断##
library(ggplot2)
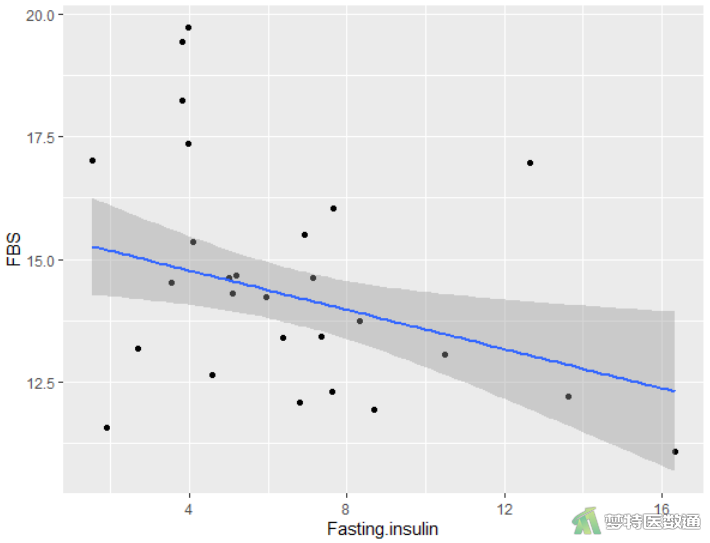
ggplot(data=mydata,aes(x=Fasting.insulin,y=FBS))+geom_point()+stat_smooth(method="lm",se=TRUE) #空腹胰岛素与空腹血糖的关系

ggplot(data=mydata,aes(x=Glycosylated.serum.protein,y=FBS))+geom_point()+stat_smooth(method="lm",se=TRUE) #糖化血清蛋白与空腹血糖的关系

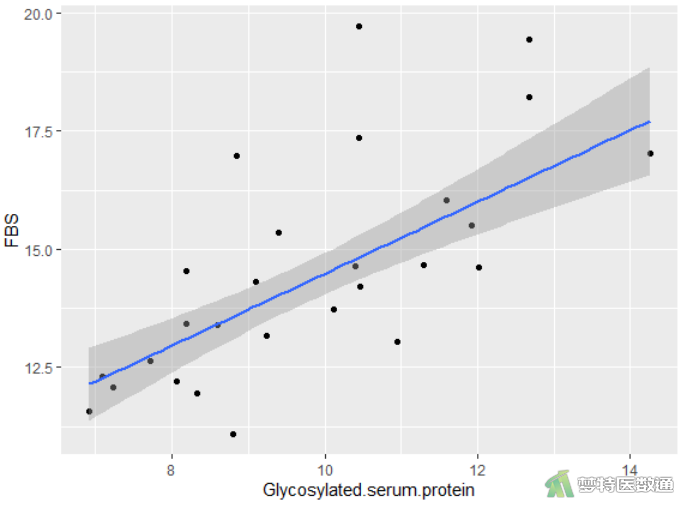
(2) 结果解读

由图3和4可知，“空腹胰岛素”、“糖化血清蛋白”与因变量之间均存在线性关系。案例数据满足条件2。

2. 条件3判断(各观测值之间相互独立)

Durbin-Watson检验通常用来检测残差是否存在自相关，Durbin-Watson检验值分布在0~4之间，越接近2，观测值相互独立的可能性越大。需要注意的是，判断观测值是否独立，主要取决于研究设计和数据收集阶段的质量控制，Durbin-Watson检验最好用于辅助判断。

(1) 软件操作

##判断独立性##
library(car)
durbinWatsonTest(lm(FBS~Fasting.insulin+Glycosylated.serum.protein+Gender+Income,data=mydata))

(2) 结果解读

图5的“durbinWatsonTest (Durbin–Watson自相关检验)” 显示，DW Statistic为1.655，P=0.27，说明观测值相互独立，本研究数据满足条件3。

3. 条件4判断(不存在显著的多变量异常值)

库克距离用来判断强影响点是否为因变量的异常值点。一般认为当D<0.5时不是异常值点，当D>0.5时认为是异常值点。

(1) 软件操作

##计算cook距离##
lm.reg<-lm(FBS~Fasting.insulin+Glycosylated.serum.protein+Gender+
Income,data=mydata) #拟合回归分析
cook<-cooks.distance(lm.reg) #计算cook距离
cook[cooks.distance(lm.reg)>0.5] #显示cook距离>0.5的个案编号和cook值
max(cook) #显示最大cook距离

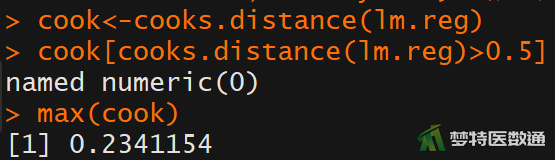
(2) 结果解读

图6“Cook’s distance (库克距离)”，最大库克距离D为0.234<0.5，提示不存在显著异常值，本研究数据满足条件4。

4. 条件5判断(多重共线性判断)

(1) 软件操作

##共线性诊断##

vif(lm.reg) #计算方差膨胀因子

(2) 结果解读

图7“vif (variance inflation factor，方差膨胀因子)”显示，所有自变量的VIF均<10，提示自变量之间不存在严重共线性问题。

5. 条件6判断(残差服从正态分布)

(1) 软件操作

##正态性检验##

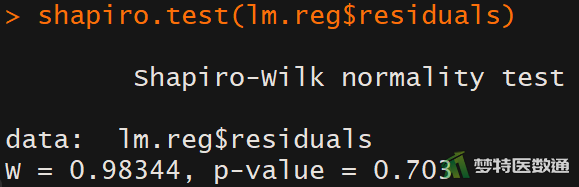
shapiro.test(lm.reg$residuals)

##Q-Q图##
qqnorm(lm.reg$residuals)  #绘制qq图
qqline(lm.reg$residuals)  #增加趋势线

(2) 结果解读

图8中“Shapiro-Wilk (夏皮罗-威尔克正态性检验)”显示，P=0.703>0.1，提示残差服从正态分布。图9残差的Q-Q图中各散点基本围绕对角线分布，也提示残差服从正态分布。因此，判定本研究数据满足条件6。

6. 条件7判断(方差齐)

(1) 软件操作

##残差图##
par(mfrow=c(2,2)) #2行2列分布
plot(lm.reg$residuals)
plot(mydata$FBS,lm.reg$residuals)
plot(mydata$Fasting.insulin,lm.reg$residuals)
plot(mydata$Glycosylated.serum.protein,lm.reg$residuals)

(2) 结果解读

图10中预测值和各变量值的残差分布较为均匀，并未出现特殊的分布形式(如漏斗或者扇形)，提示残差的方差齐，本研究数据满足条件7。

(三) 变量筛选

1. 逐步回归法

AIC(Akaike Information Criterion，赤池信息准则)考虑了模型的统计拟合度以及用来拟合的参数数目，可以用来比较模型。 AIC值越小的模型表明用较少的参数获得了足够的拟合度，可优先选择。

变量的选择一般采用逐步回归，模型会每次添加或删除一个变量，直到达到某个判停准则为止。MASS包中的stepAIC()函数可以实现模型的逐步回归(向前、向后和向前向后)，依据的是精确AIC准则。

(1) 软件操作

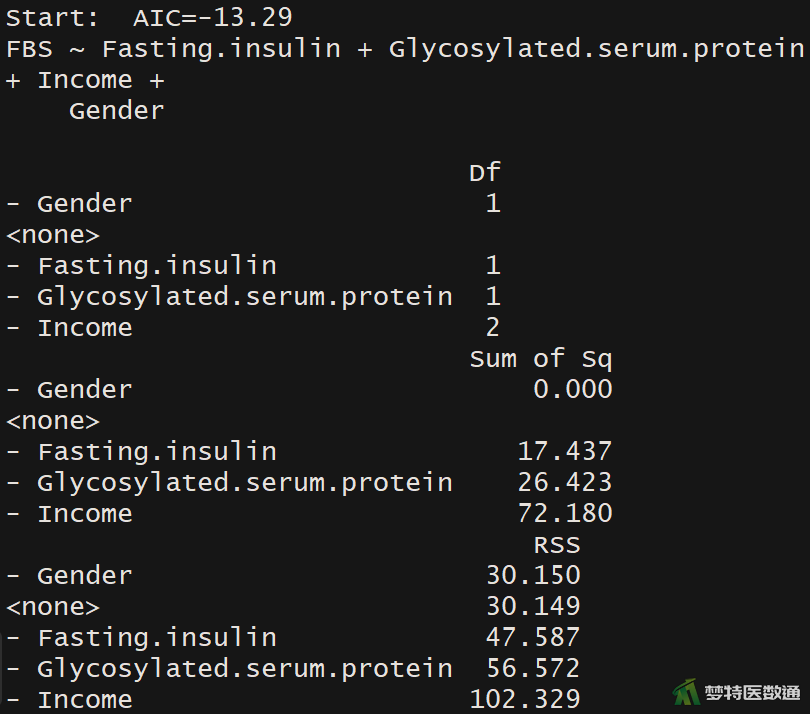
##逐步回归筛选变量##
library(MASS) #调用包“MASS”
stepAIC(lm.reg,direction = "backward") #向后法逐步回归

(2) 结果解读

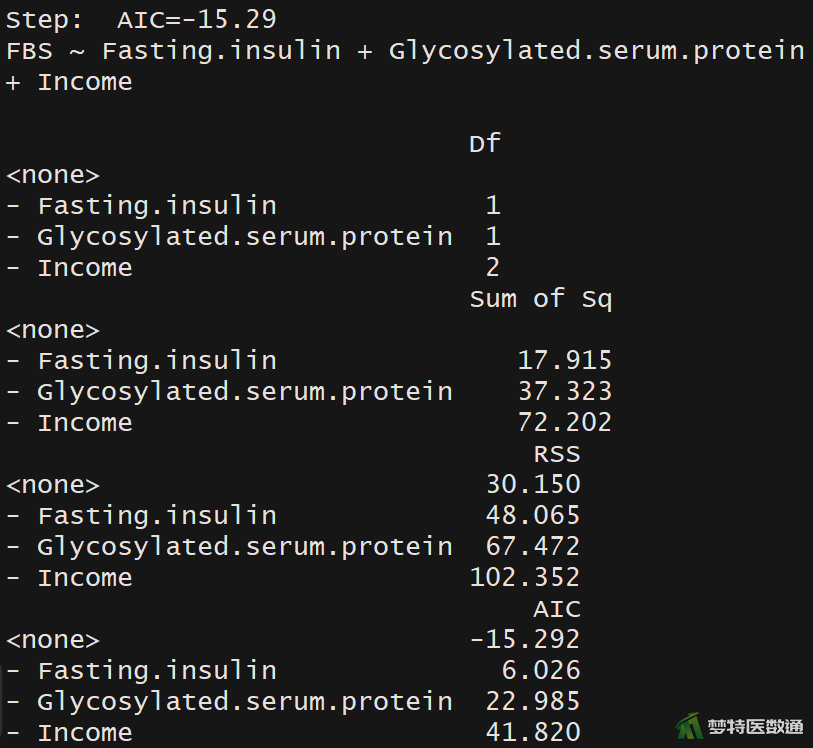
图11-1与图11-2分别显示了逐步回归的初始模型与终止模型，根据AIC信息准则，终止模型中去除了“性别(Gender)”这一变量后，AIC减小，提示应将“Gender”移除模型，即在模型中保留“空腹血糖”、“糖化血红蛋白”和“收入”。

2. 层次回归法

通过逐个增加自变量的方法建立多个模型，以查看每个自变量与因变量的关联是否有统计学意义；另外对多个模型进行比较，以确定最佳的模型。

(1) 软件操作

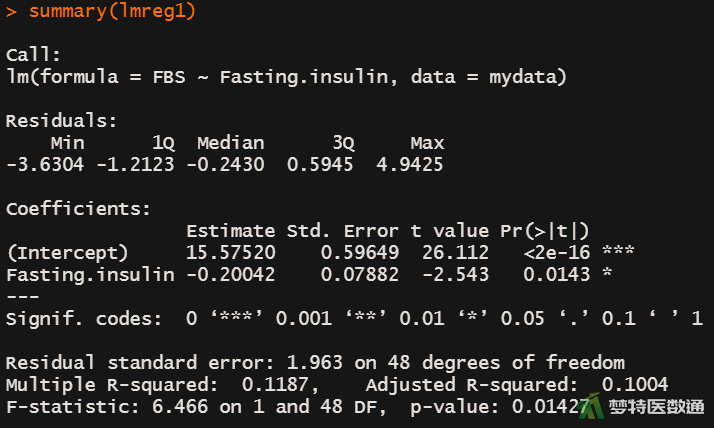
##拟合多个模型##
lmreg1<-lm(FBS ~ Fasting.insulin, data=mydata) #空腹血糖
lmreg2<-lm(FBS ~ Fasting.insulin + Glycosylated.serum.protein, data=mydata) #空腹血糖+糖化血清蛋白
lmreg3<- lm(FBS ~ Fasting.insulin + Glycosylated.serum.protein + Income, data=mydata) #空腹血糖+糖化血清蛋白+收入
lmreg4<- lm(FBS ~ Fasting.insulin + Glycosylated.serum.protein + Income + Gender, data=mydata) #空腹血糖+糖化血清蛋白+收入+性别
##输出多个模型的结果##
summary(lmreg1) 

summary(lmreg2)

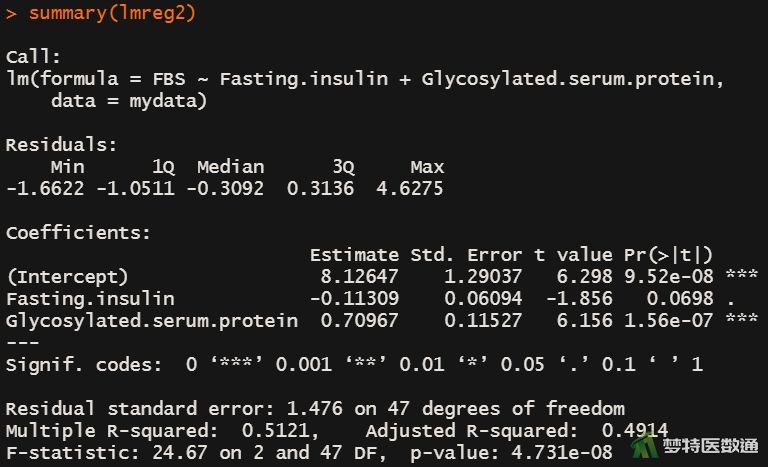
summary(lmreg3)

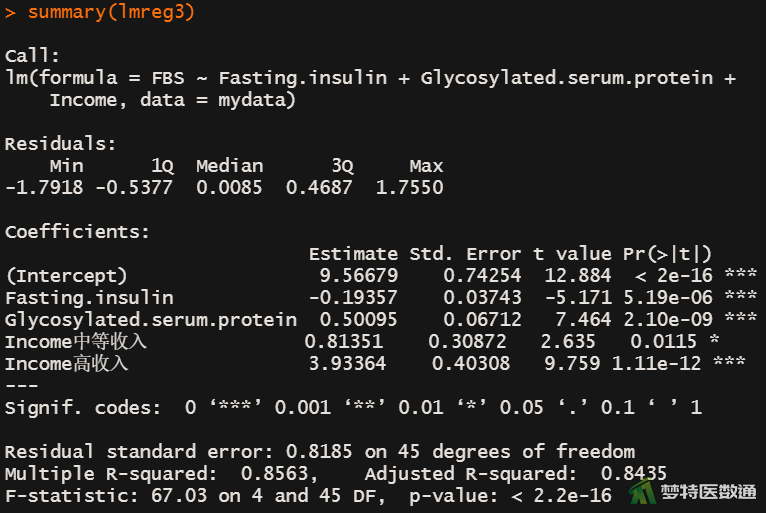
summary(lmreg4)

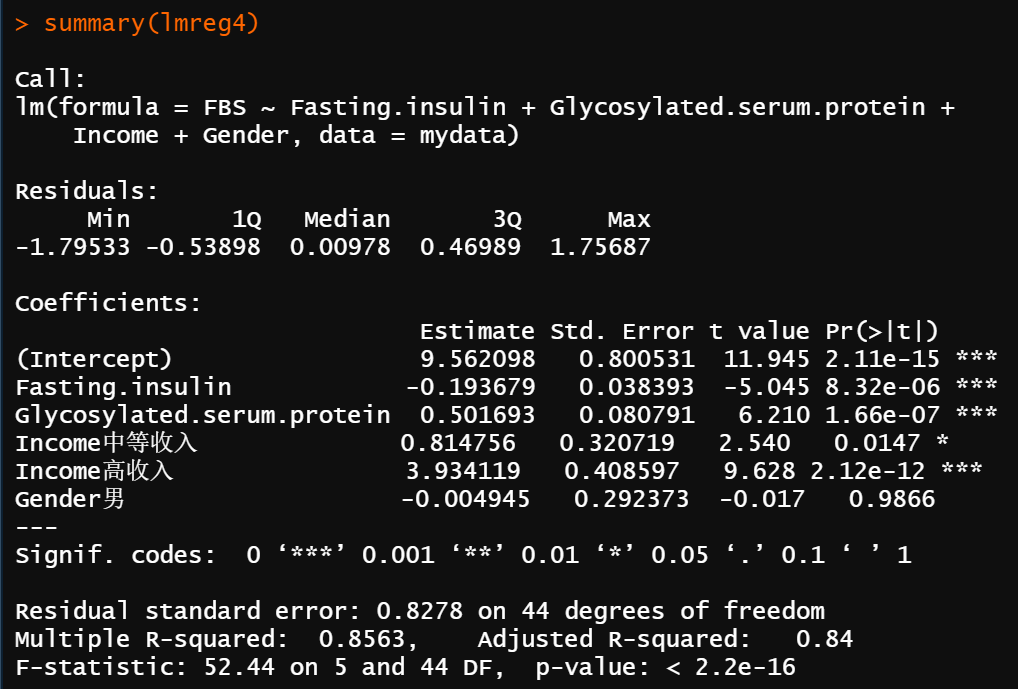
##对多个模型进行比较##

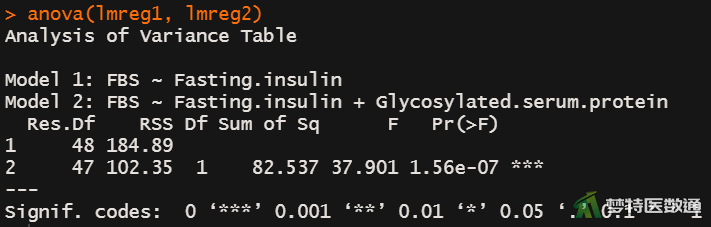
anova(lmreg1, lmreg2)

anova(lmreg2, lmreg3)

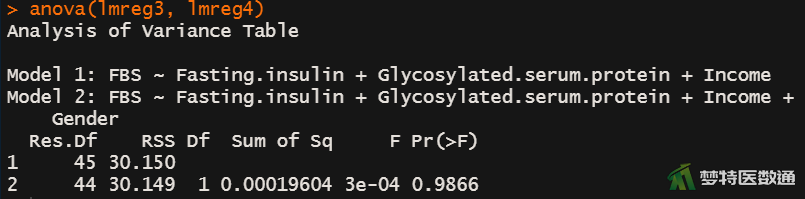
anova(lmreg3, lmreg4)

(2) 结果解读

由图12-1至图12-4结果可知，在4个模型中变量Fasting.insulin、Glycosylated.serum.protein、Income均有统计学意义(第2个模型中Fasting.insulin的P值为0.0698，为marginal significant)，在第4个模型中Gender与FBS的关联无统计学意义。由图13-1至图13-3中结果可知，lmreg2与lmreg1相比、lmreg3与lmreg2相比，差异均有统计学意义(P<0.001)；但lmreg4与lmreg3相比，差异无统计学意义(P=0.987)。结合lmreg中Gender无统计学意义，说明变量Gender应从模型中移除。

(四) 模型拟合

将变量“性别”从模型中去除，进行模型拟合分析。

1. 软件操作

##建立移除性别变量之后的回归模型##

lmreg.new<-lm(FBS ~ Fasting.insulin + Glycosylated.serum.protein + Income, data=mydata) #仅移除性别

##展示拟合模型的详细结果##

summary(lmreg.new) 

##计算模型中变量系数的95%CI##

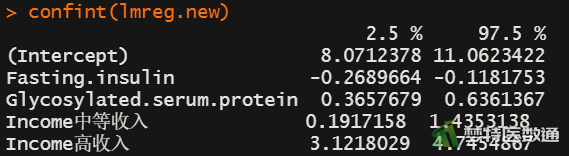
confint(lmreg.new)

2. 结果解读

(1) 拟合优度

由图14可知，最终模型的决定系数为0.856，校正决定系数为0.844，均方根误差为0.819，表明模型整体拟合较好。

(2) 模型系数

图14的Coefficients部分列出了截距和自变量的“Estimate (非标准化系数)”、“Std.Error (标准误)”，统计量t值及P值。结果显示模型中的所有自变量均有统计学意义(P<0.001)。图15则显示了模型lmreg.new的所有变量系数的95%CI。

回归模型的截距为9.567，表示自变量取值为0时，因变量的取值，并无实际专业意义。变量“空腹胰岛素”的非标准化系数(即斜率)为-0.194 (95%CI：-0.269~-0.118，P<0.001)，表示“空腹胰岛素”每增加1mmol/L，空腹血糖减少0.194 mmol/L；变量“糖化血清蛋白”的非标准化系数(即斜率)为0.501 (95%CI：0.366~0.636，P<0.001)，表示“糖化血清蛋白”每增加1%，空腹血糖增加0.501 mmol/L。相比“低收入”人群而言，“中等收入”人群的非标准化系数为0.814(95%CI：0.192~1.435，P=0.015)，表示“中等收入”人群比“低收入”人群空腹血糖高0.814 mmol/L；相比“低收入”人群而言，“高收入”人群的非标准化系数为3.934 (95%CI：3.122~4.745，P<0.001)，表示“高收入”人群比“低收入”人群空腹血糖高3.934 mmol/L。

据此可以写出本案例的回归方程为：

空腹血糖 = 9.567 - 0.194×空腹胰岛素 + 0.501×糖化血清蛋白+ 0.814×(经济水平=中等收入) + 3.934×(经济水平=高收入)

根据此方程输入相关自变量数值即可对空腹血糖进行预测。

四、结论

本研究采用多重线性回归模型考察“空腹血糖”是否受到性别、经济水平、空腹胰岛素和糖化血清蛋白的影响。通过绘制散点图，提示空腹胰岛素和糖化血清蛋白与空腹血糖之间存在线性关系，通过专业判断和Durbin-Watson检验提示数据之前相互独立，通过库克距离分析，提示数据不存在需要删除的异常值；通过方差膨胀因子和容忍度判断自变量之间不存在严重多重共线性，通过Shapiro-wilk检验及绘制残差Q-Q图，提示残差服从正态分布；通过绘制残差图，提示残差方差齐。满足多重线性回归分析条件。

多重线性回归分析结果解读为，在其他变量不变的情况下，“空腹胰岛素”每增加1mmol/L，空腹血糖减少0.194 mmol/L (β=-0.194，95%CI：-0.269~-0.118；P<0.001)；“糖化血清蛋白”每增加1%，空腹血糖增加0.501 mmol/L (β=0.501，95%CI：0.366~0.636；P<0.001)；“中等收入”人群比“低收入”人群空腹血糖高0.814(β=0.814，95%CI：0.192~1.435，P=0.011)；“高收入”人群比“低收入”人群空腹血糖高3.934 (β=3.934，95%CI：3.122~4.745，P<0.001)。

线性回归分析方程为：

空腹血糖 = 9.567 - 0.194×空腹胰岛素 + 0.501×糖化血清蛋白+ 0.814×(经济水平=中等收入) + 3.934×(经济水平=高收入)。回归模型具有统计学意义，F=67.03，P<0.001；模型可以解释84.4%的因变量的变异(adjusted R²=0.844)。

五、分析小技巧

(一) 各观测值之间的独立性检测

判断观测值是否独立，主要取决于研究设计和数据收集阶段的质量控制，Durbin-Watson检验最好用于辅助判断。Durbin-Watson检验值分布在0~4之间，越接近2，观测值相互独立的可能性越大。且根据Pr <DW和Pr >DW，可得知正相关检验和负相关检验的P值大小，更容易客观的判断独立性。

(二) 异常值检测

• Cook’s D(库克距离)用来判断强影响点是否为因变量的异常值点。一般认为当D<0.5时不是异常值点，当D>0.5时认为是异常值点。
• 并非所有的异常点都意味着结果不好，有时候发现异常点可能会提示有更重要的信息。如果出现异常点，首先应检查数据是否录入错误，也可以选择其他相应模型来拟合，或者需要收集更多的数据来证实。

(三) 残差的正态性检测

如果残差不符合正态分布，可以考虑对因变量进行数据变换，使其服从正态分布后再拟合线形回归模型。

(四) 残差的方差齐性检测

残差的方差齐是指在自变量取值范围内，对于任意自变量取值，因变量都有相同的方差。线形回归中，残差的方差齐实际上要比残差正态分布重要。如果这一条件不满足，可对因变量进行变量变换，使其满足残差方差齐，也可以采用加权回归分析，消除方差的影响。

(五) 变量筛选

• 多重回归分析中，变量的筛选一般有向前筛选(selection=forward)、向后筛选(selection=backward)、逐步筛选(stepwise)三种基本策略。
• 向前筛选是变量不断进入回归方程的过程。首先，选择与因变量具有最高线性相关系数的变量进入方程，并进行回归方程检验；其次，在剩余的变量中寻找与因变量偏相关系数最高的变量进入回归方程，并对新建立的回归方程进行检验；一直重复这个过程，直到再也没有可进入方程的变量为止。
• 向后筛选是变量不断剔除出回归方程的过程。首先，所有变量全部引入回归方程，并对回归方程进行检验，然后在回归系数不显著的变量中，剔除t检验值最小的变量，并对模型进行检验；直到回归方程中所有变量的回归系数均显著，则回归模型确定。
• 逐步筛选在向前筛选的基础之上，结合向后筛选策略，在每个变量进入方程后再次判断是否存在可以剔除方程的变量。因此，逐步筛选在引入变量的每一个阶段都提供了剔除不显著变量的机会。

(六) 回归模型

在进行回归分析时，要注意避免对数据的过渡挖掘，不能将回归模型分析的结果随意延伸到自变量取值范围以外的数值。也不能随意将模型分析结果延伸到因果关系。

(七) 模型评价

常见的回归模型评价指标有：决定系数R²、校正决定系数adjusted R²和均方根误差RMSE等。实际分析时，可以综合多个指标，并结合模型所反映的实际情况来判断。

• 决定系数R² (determination coefficient)反映了因变量的变异能够被自变量解释的比例，或者说方程中的自变量解释了因变量变异的多少。R²越大，表示方程中自变量解释能力越强。但该指标有一缺陷，即其值随着自变量的增多而增加，即使加入无意义的变量，该指标值也会随之增加，因此不能较好地反映模型优劣。
• 校正决定系数adjusted R²(adjusted determination coefficient) 是对决定系数的修正。当有统计学意义的变量进入方程时，该指标随之增大，而当无统计学意义的变量进入方程时，其值减小。值越大表明模型越好，是衡量模型优劣的重要指标之一。
• 均方根误差RMSE主要反映模型的估计精度，值越小越好。一般会随模型中自变量个数增加而减小，这一性质与校正系数相似。